贪心 · Greedy Algorithm
田忌赛马
-
如果田忌目前的最快马快于齐王目前的最快马,则两者比
-
如果田忌的最快马慢于齐王的最快马,则用田忌的最慢马与齐王的最快马比 减少损失)
-
如果田忌的最快马和齐王的最快马相等,分以下两种情况:
- 若田忌的最慢马快于齐王的最慢马,两者比(能赢就赢呗)
- 其他,用田忌的最慢马与齐王的最快马比(贡献最大)
Code
#include<bits/stdc++.h>
using namespace std;
const int N=2001;
int a[N],b[N];
int main() {
int Ans,n,la,lb,ra,rb,i;
scanf("%d",&n);
for (i=1;i<=n;++i)
scanf("%d",a[i]);
for (i=1;i<=n;++i)
scanf("%d",b[i]);
sort(a+1,a+n+1);
sort(b+1,b+n+1);
Ans=0,la=lb=1,ra=rb=n;
for (i=1;i<=n;++i) {
if (a[ra]>b[rb]) Ans+=200,--ra,--rb;
else if (a[ra]<b[rb]) Ans-=200,++la,--rb;
else if (a[la]>b[lb]) Ans+=200,++la,++lb;
else {
if (a[la]<b[rb]) Ans-=200;
++la,--rb;
}
}
printf("%d\n",Ans);
return 0;
}1-02E. JM的西伯利亚特快专递
Code
#include <bits/stdc++.h>
using namespace std;
int a[100005],sum[30],cnt=0,ans[100005];
int main() {
stack <int> t;
string s;
cin >> s;
int n = s.length();
for(int i = 0;i < n;i ++) {
a[i + 1] = s[i] - 'a' + 1;
}
for(int i = 1;i <= n; i++) {
sum[a[i]] ++;//统计S中各个字母出现的次数
}
int idx=1;
for(int i=1;i<=n;i++) {
while(!sum[idx]) //找到S中字典序最小的字母
idx++;
while(!t.empty()&&t.top()<=idx) { //如果T的顶部数字字典序比这个数小
ans[++cnt]=t.top();
t.pop();
}
if(a[i] == idx) { //如果要放的这个数是 S中字典序最小的字母
ans[++cnt]=idx;
sum[a[i]]--;
}
else { //等待idx的出现
t.push(a[i]);
sum[a[i]]--;
}
}
while(!t.empty()) { //T中的残余字母无法最优
ans[++cnt]=t.top();
t.pop();
}
for(int i=1;i<=cnt;i++)
printf("%c",ans[i]+'a'-1);
return 0;
}
CF1175E Minimal Segment Cover
Code
#include<bits/stdc++.h>
using namespace std;
const int N=600005;
int n,m,l,r,ma,a[N],f[N][22];//从一个左端点用pow(2,j)条线段最远能覆盖到哪个右端点
int main()//注意线段起点可能在这个左端点左边 !!!
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&l,&r);
a[l]=max(a[l],r); //原始线段左端点所能覆盖的最大
ma=max(ma,r);
}
for(int i=1;i<=ma;i++) a[i]=max(a[i],a[i-1]); //用一根线段,如果i-1最远覆盖的右端点比i多,显然i-1会包含i
for(int i=0;i<=ma;i++) f[i][0]=a[i];//跑完这个程序相当于得到每个左端点所能覆盖的最大
for(int i=1;i<=20;i++)
for(int j=0;j<=ma;j++)f[j][i]=f[f[j][i-1]][i-1];//走pow(2,j)等于走pow(2,j-1)再走pow(2,j-1)
while(m--)
{
scanf("%d%d",&l,&r);
int ans=0;
for(int i=20;i>=0;i--)
if(f[l][i]<r) {
ans+=1<<i;
l=f[l][i];
}
if(a[l]>=r)printf("%d\n",ans+1);
else puts("-1");
}
return 0;
}
CF1707A Doremy's IQ
防晒霜
贪心+排序
我们首先将奶牛可以承受的最大值,从小到大排序,
然后将防晒霜固定的值,从小到大
对于每一个头奶牛而言,当然是要选择目前来说满足条件的最差的防晒霜,什么最差的定义,就是选择满足奶牛条件的SPF最小的那一瓶防晒霜.
如下图,两段轴是排过序的,红色部分是符合前一段条件的牛
①③显然无影响,但②体现了,值越大的防晒霜,有可能让更多的牛使用
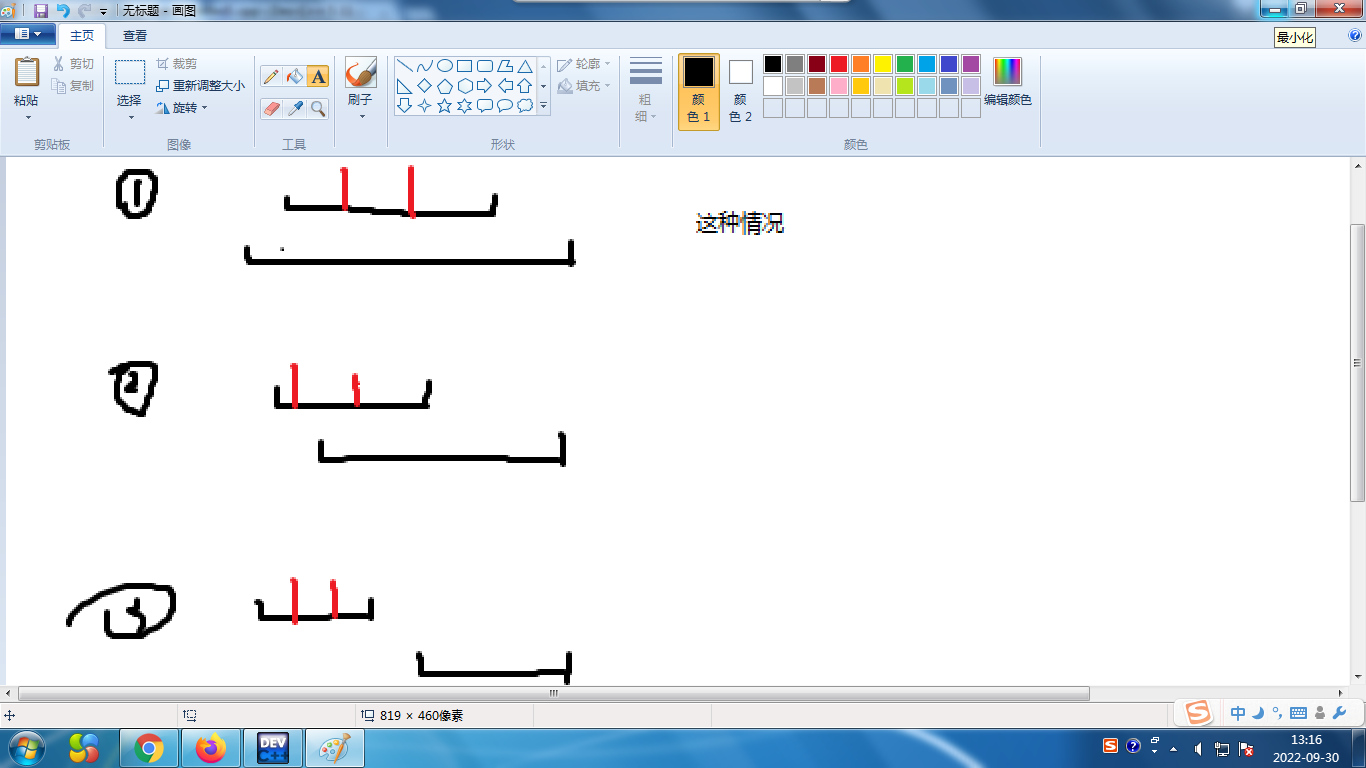
为什么不能将左端点从小到大排序?
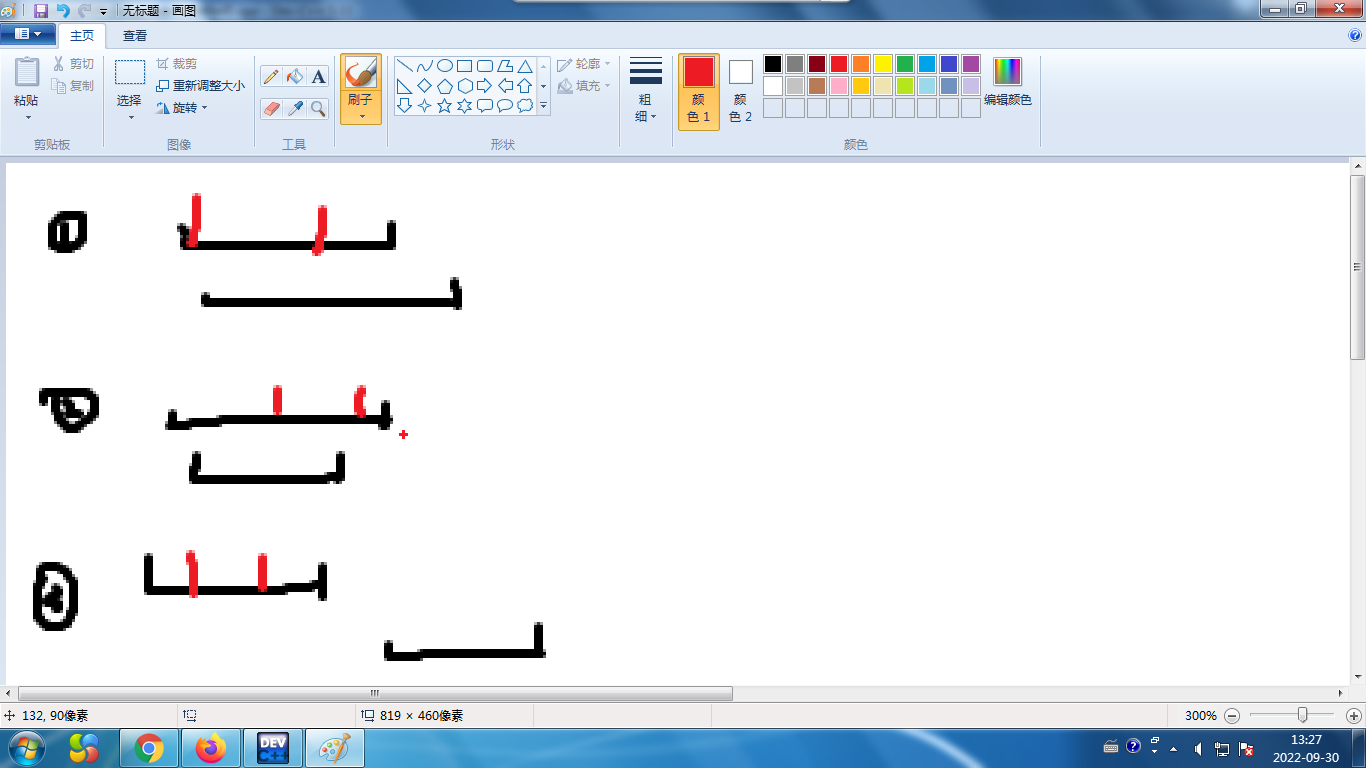
对于第②种情况,显然先选靠后的会更优
跳跃游戏
首先,解题之前得理解清楚这个题的意思。从题目中可以获悉:对于数组中任意一个位置y, 想要判断它是否可以到达,只需要存在一个位置x,在保证其本身可达的前提下,它跳跃的最大长度为 x + num[x]。也就是说,需要满足条件:x + num[x] >= y。 因此,对于每一个可以到达的位置 x,它使得从x 到 x + nums[x] 范围内的这些连续的位置都可以到达。
通过上述分析:首先,依次遍历数组中的每一个位置,并实时获取最远可以到达的位置。对于当前遍历到的位置 x,如果它在最远可以到达的位置的范围内,那么就可以从起点通过若干次跳跃到达该位置,因此我们可以用x + num[x] 更新最远可以到达的位置。在遍历的过程中,如果 最远可以到达的位置大于等于数组中的最后一个位置,那就说明最后一个位置可达,直接返回 True 。反之,如果在遍历结束后,最后一个位置仍然不可达,就返回 False 。
如下图:
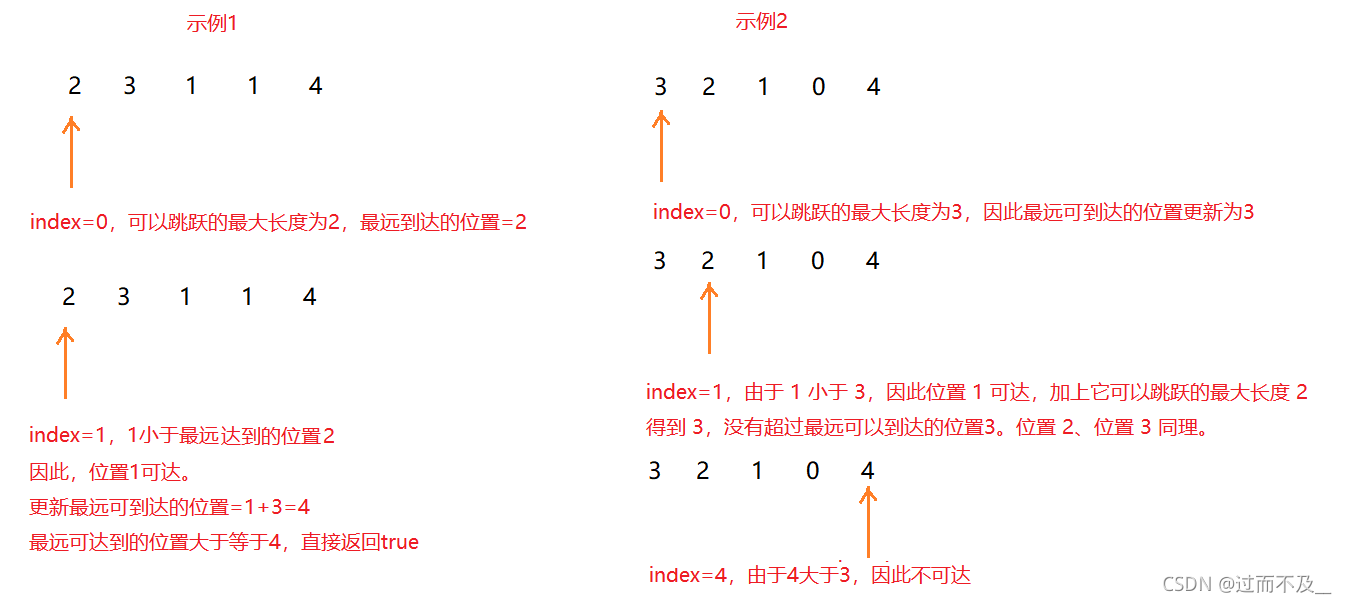
本文来自博客园,作者:Doria_tt,转载请注明原文链接:https://www.cnblogs.com/pangtuan666/p/16529874.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号