二叉堆 の 概念及其运用

  习惯上，我们将二叉堆简称为"堆"。堆是由数组存储的完全二叉树，是一种实现优先队列(priority_queue)的数据结构。 所谓优先队列，是允许插入(insert)元素，查询最优元素(最大元素或最小元素)，删除元素的三种操作。 堆在NOIP竞赛中应用广泛，常用与快速查询最大(最小值)，优化各种算法(如:最短路算法、DP算法)，是一种效率高，应用广泛的数据结构。 

1.概念

完全二叉树： 

  如果一棵深度为k的二叉树，1至k-1层都是满的，即每层结点数满足2^i-1，只有最下面一层的结点数小于2^i-1，并且最下面一层的结点都集中在该层最左边的若干位置，则此二叉树称为完全二叉树。 

                                                   

二叉堆： 

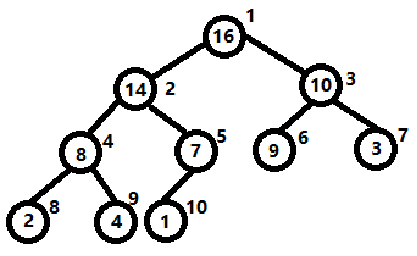
  二叉堆是一种数组对象，它可以被视为一棵完全二叉树。树中每个结点与数组中存放该结点中值的那个元素相对应，如图。

                 

 

 2.二叉堆的性质 

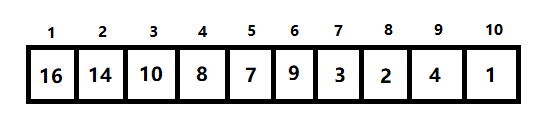
  设数组A的长度为len，二叉树的结点个数为size，size≤len，则A[i]存储二叉树中编号为i的结点值(1≤i≤size)，而A[size]以后的元素并不属于相应的堆，树的根为A[1]，并且利用完全二叉树的性质，我们很容易求第i个结点的父结点fa(i)、左孩子lch(i)、右孩子rch(i)的下标，分别是i/2、2i、2i+1。 

大根堆： 

  二叉堆还具有这样一个性质：对除根以外的每个结点i，A[fa(i)]≥A[i]。即除根结点以外，所有结点的值都不得超过其父结点的值，这样就推出，堆中最大元素存放在根结点中，且每一结点的子树中的结点值都小于等于该结点的值，这种二叉堆又称为“大根堆”；反之，称为“小根堆”。 

 

3.二叉堆的操作 

  堆一般有两个重要的操作，put(往堆中加入一个元素)和get(从堆中取出并删除一个元素) 

  put操作(也可用于建堆，我们以创建一个小根堆为例) 

    1、在堆尾加入一个元素，并把这个结点置为当前结点。

    2、比较当前结点和它父结点的大小 。如果当前结点小于父结点，则交换它们的值，并把父结点置为当前结点，继续转2。 如果当前结点大于等于父结点，则转3。 

    3、结束。 

  重复n次put操作，即可建立一个小根堆，我们举个例子： 

  输入n=10的10个int数据：3 5 1 7 6 4 2 5 4 1，建立小根堆。

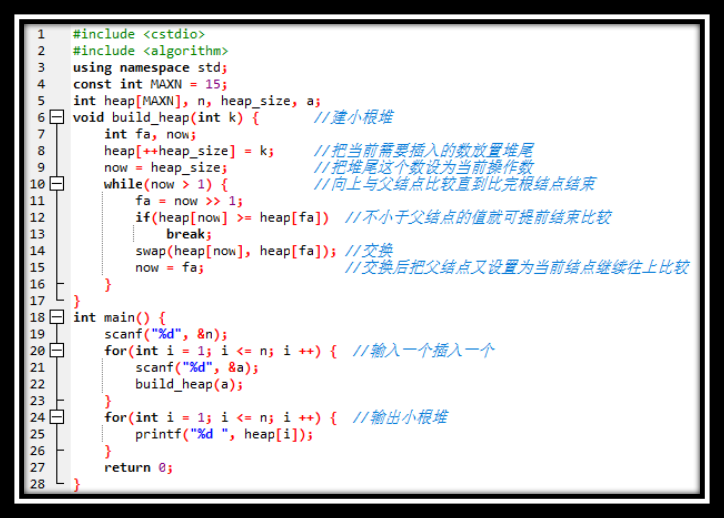
  设一个堆结构heap[MAXN]，插入一个数进入堆尾，堆尾下标heap_size+1，把堆尾下标赋给now，设定为当前要操作数的下标，现在将now不断向上与父结点比较(heap[now]<heap[now/2]，就要交换，并把now>>=1)，直到比完根节点heap[1]或者大于等于父结点了就结束。

                           

 

 

 从堆中取出并删除一个元素的get操作： 

  1、取出堆中根结点的值。

  2、把堆的最后一个结点(heap_size)放到根的位置上，把根覆盖掉，堆长度减一。

  3、把根结点置为当前父结点，即当前操作结点now。

  4、如果now无儿子(now>len/2)，则转6；否则，把now的两(或一)个儿子中值较小的那一个置为当前子结点son。

  5、比较now与son的值，如果now的值小于等于son，转6；否则交换两个结点的值，把now指向son，转4。

  6、结束。 

 

Show Time

  Sequence

  No.1堆排序

  1、在输入n个无序数时，输入一个数，插入到堆中一个数，形成数组建堆操作，由于该题要求从小到大排序，所以建立小根堆；  

  2、最后用一重n次的循环依次取出并删除根结点就行了，即执行get操作。  

时间复杂度：O(N*log₂N) 

Code

 #include <bits/stdc++.h>
using namespace std;
int n,a[100005],size;
 
void Put(int k) {
	a[++size]=k;
	int len=size;
	while(len>1 && a[len]<a[len>>1])
		swap(a[len],a[len>>1]),len>>=1;
	return ;
}
 
void Get() {
	printf("%d ",a[1]);
	a[1]=a[size--];
	int now=1;	
	while(now*2<=size) {
		int son=now*2;
		if(son<size && a[son+1]<a[son]) son++;
		if(a[now]>a[son]) swap(a[now],a[son]);
		else break;
		now=son;
	}
	return ;
}
 
int main() {
	scanf("%d",&n);
	for(int i=1,t;i<=n;i++)
		scanf("%d",&t),Put(t);
	for(int i=1;i<=n;i++) Get();
	return 0;
}