洛谷 P3629 [APIO2010] 巡逻 =＞ 保姆级题解

前置知识

树的直径

思路

首先，通过题目的样例和题面描述，我们可以得知，在不添加任何边的情况下，帽子叔叔巡逻整个村子要走 \(2 \times (n-1)\) 条边，解释一下，就是每条边都会走 \(2\) 遍，又因为有一颗树有 \(n-1\) 条边，所以就是 \(2 \times (n-1)\)

接着观察数据规模，\(1 \le k \le 2\)，所以 \(k\) 只能是 \(1\) 或者 \(2\)，所以我们可以根据 \(k\) 的取值来判断解法。

\(k = 1\)

很明显，如果我们根据贪心的思想，我们一定会把这条边加在树上距离最远的 \(2\) 点。而树的直径刚好符合这个条件。所以我们直接求树的直径就可以。但树的直径的求法就有 \(2\) 个，两次 dfs 和 dp，我们要选哪一个呢？

当然是两次 dfs。因为在 前置知识 中，我们已经讲过 dp 的做法只能求路径长度 (如果可以评论区说一下哈)，而 dfs 能把树的直径的 \(2\) 个端点和路径都求出来，所以我们选 dfs。

当然，有同学可能会说，这里又不涉及路径，dp 也可以呀。确实可以，但是为了方便，因为 \(k=2\) 也要路径和端点，所以我们用 dfs。

那问题来了，求出直径后，答案是多少？

我们回到最初添边的目标，让巡逻的边数减少，换句话说，减少重复经过的边。接下来，我们要知道一个树有 \(n\) 个节点和 \(n-1\) 条边，增加一条边，就是 \(n\) 个节点 \(n\) 条边，这是一个基环树 (基环树定义：有 \(n\) 个节点和 \(n\) 条边的树)，所以添了一条边之后，树中会呈现一个环，而这个环，除了我们添的边，其他边都是树的直径。因此，如果树的直径为 \(d\)，那么这个环的边数就是 \(d + 1\)

所以，我们说了这么多要干啥呢？没错，通过以上的推论，我们会惊奇的发现，有了这个环，会让我们在巡逻的过程中只走过一次这些边 (这些边指环上的边)。这一点很好证明。

因为巡逻的起始点是 \(1\)，而树的直径必定经过 \(1\)，因为树的直径可以看作某个节点向 \(2\) 个方向向下延伸，所以，我们把这个 “某个节点” 看作根节点。从 \(1\) 出发，延着环巡逻，如果当前点 \(u\) 旁边有节点未巡逻，那么就走进去，最终还是会回到 \(u\)，而且，那些未被巡逻的点不是环上的边，否则，如果走下去，又会回到 \(1\) 节点。所以环上的边只会路经一次。

回到我们前面说的，这个环有 \(d\) 条边 ( \(d\) 的定义见前面) 是树的直径，树的直径的长度就是 \(d\)，所以这 \(d\) 条边我们只用走 \(1\) 次，少走了多少呢？原本没有这个环，每条边都要走 \(2\) 次，\(d\) 条边就是 \(2d\) 次，而现在是 \(d\) 次，所以少了走了 \(2d - d = d\) 条边，但这还不够，因为我们多添了一条边，而这 \(1\) 条边我们必须经过 (题面中说新增的边必须走过一次，而且只有一次)，所以在答案的最后，我们还要 \(+1\)。

因此 \(k=1\) 的答案就是 \(2 \times (n-1) - d + 1\)，即原来要走的步数减去少走的步数，最后加上我们新添的那一条边，也就是一步。

\(k = 2\)

前面 \(k = 1\) 说了那么久，就是为了 \(k = 2\)。对于这种情况，我们还是贪心，选择次长的树的直径。然后再连边，再求答案。但是这种贪法我们要进行分类讨论，因为 \(k=1\) 可以保证答案正确，但 \(k=2\) 不可以。我们假设树的直径为 \(d_1\)，次长于树的直径的长度为 \(d_2\)，那么添边后会出现 \(2\) 个环，那么这 \(2\) 个环可能会有如下关系：

1. \(2\) 个环无公共边。
2. \(2\) 个环有公共边。
3. \(1\) 个环包含另一个环。

我们拿样例举例子：

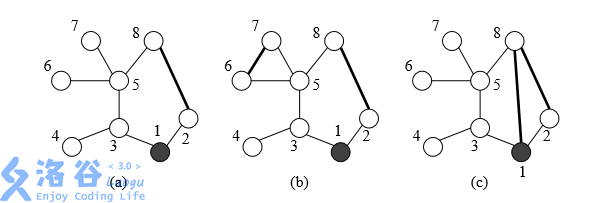
首先看 (c)，它对应情况 (3)，巡逻的最小距离为 \(15\)，我们要排除 \(c\) 这种可能。为什么？因为这样只会使答案更劣，因为处于外面的环走一遍就好了，但因为 \(2\) 个环有了包含关系，所以我们还有再从新加的边开始再走一边环，这样子明显会使答案更劣，所以直接排除。

接下来看 (b)，它对应情况 (1)，两个环无公共边，巡逻的最小距离为 \(10\)，这种情况使我们想要的。为什么？因为它就像 \(k=1\) 一样，帮我们又把一些边的访问次数降到了 \(1\)，从而使得巡逻的边数减少。而且 \(2\) 个环无公共边，也就不用把一些边走 \(2\) 次了。

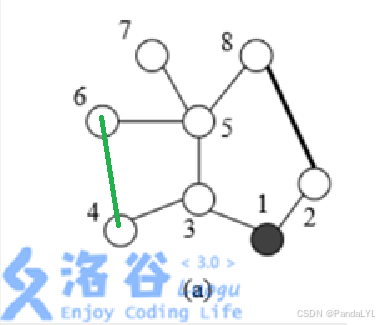
最后来看这个图，我们在 \(4\) 和 \(6\) 之间连了一条边，此时对应第 \(2\) 种情况，图中的 \(2\) 个环有公共边 ( \(3\) 和 \(5\) 之间的边) 。这种情况也不是我们想要的。因为题目中说新增的边都要走一次，而为了这一条边，我们要把整个环遍历一遍，因为我们最终会回到进入环时的那个节点，所以说，图中的 \(edge(3,5)\)，即 \(3\) 和 \(5\) 之间的边会被位于它左边的环和右边的环一共遍历 \(2\) 次，这也不是我们想要的，居然环上有边要遍历 \(2\) 次，那我们要这个环干啥呢？

所以，我们在找次短直径的时候，不要和第一个环有公共边，意思就是说第一个环的边在第二次求次短直径时不能有。这该怎么办呢？我们先把这些边去掉，看看会怎么样。

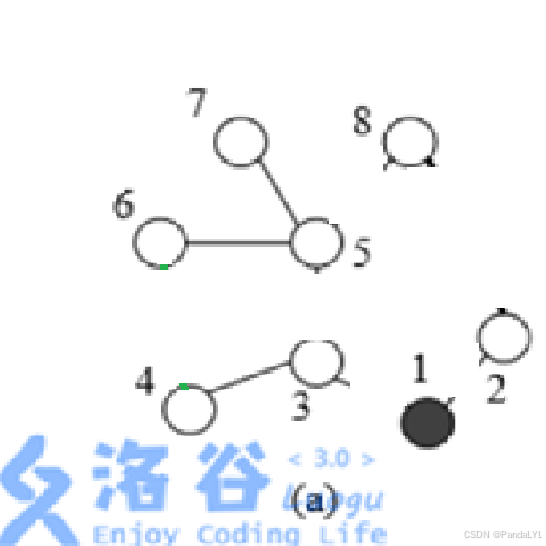
此时很明显，次短直径是 \(6->5->7\) 的这 \(2\) 条边。如果把这些边删掉会影响我们求 \(d_2\)，所以我们可以给边赋值来保证答案准确性。显然，赋的值不能 \(>0\)，这样不仅求的过程会受影响，其次答案也会不准确。赋的值如果 \(=0\) 呢？就拿 \(7->5->3->4\) 这 \(3\) 条边举例子。如果直径的边为 \(0\)，那么这三条边的权值之和为 \(2\)，也就是说 \(7->5->3->4\) 是次长直径，但是你一连，发现和原来的环有公共边。这是因为如果第一个环的边权为 \(0\)，一直加下去，答案一定 \(>0\)，但是在加起来的过程，有几条边不能连在一起，比如 \(edge(7,5)\) 和 \(edge(5,3)\) (在下面 \(edge(u,v)\) 表示 \(u\) 和 \(v\) 之间的边) 不能连在一起，因为又会出现公共边。所以赋值为 \(0\) 不可取。

最后就是 \(<0\)，先排除 \(\le -2\) 的值，因为这样答案会过小，例如 \(1 + (-2) = -1\)，后面如果又有一个 \(-2\)，那岂不是无休止的负数？而且改成 \(\le -2\)，就以为着一条在环上的边等价于好几条不在环上的边，这很不合理。

所以，我们要推出最终的选择，就是**给环上的每个值赋成 \(-1\)。下面来讲述理由 (这一块很多 OIER 写题解时都没怎么讲清楚，导致一些同学可能很疑惑)。

首先，如果在计算 \(d_2\) 的过程中遇到负数，那么加上这条边就会使答案不是最大的，也就意味着算上有环的边的答案不可能是最大的，除非只能跟原来的环有公共边。这样子的话，环上的一条边就等价于不是环上的一条边。这个时候再算 \(7->5->3->4\)，就会得到 \(1 + (-1) + 1 = 1\)，相当于要用不是环上的边抵消环上的边。那这个时候可能又有同学问了，那有可能最终算出来的结果可能比我们要求的次短直径大或者小，怎么保证它一定是准确的。

这是一个很好的问题，想要回答这个，我们要回到处理公共边的时候。

那个时候，因为两个环有公共边，而公共边又要被走 \(2\) 次，所以我们对待公共边有 \(2\) 种选择，不走或者减去。而公共边之所以是公共边也是有道理的，因为它没法当连接直径 \(2\) 端的线段，否则树的直径不可能那么短，如果可能，那这颗树就非常的抽象，因为有 \(2\) 个节点之间没有边，导致树被它们分成了 \(2\) 块，那个时候它就不是树，它是两个图的集合，这明显不可以 (大家可以自己画一下)。

所以我们尽量选择不走公共边，那么答案也就要减去公共边的数量。即 \(ans = 2 \times (n-1) - d_1 + 1 - d_2 + 1 - x\)，\(-d_2 + 1\) 是跟 \(d_1\) 一样的，不清楚的同学可以爬楼。\(x\) 指公共边的数量。但是我们不知道公共边有多少条呀，所以把环上的边权都设为了 \(-1\)，因为到时候都要减，那就干脆现在减。

回到我们的题目，因此，我们求的 \(d_2\) 并不是 \(d_2\)，它其实已经在帮答案减去 \(x\) 了。

那么答案就是 \(2 \times (n-1) - d_1 + 1 - d_2 + 1 = 2 \times n - 2 + 2 - d_1 - d_2 = 2n - d_1 - d_2\)

注意，这里的 \(d_2\) 可是融合了 \(x\) 的 \(d_2\)

根据我们的前置知识，dfs 的做法遇到负边权就会 GG，所以这里我们用 dp 的做法，前面因为要求路径，所以用 dfs 的求法。

PS:

有不明白的地方在评论区及时提出 😃

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

int read() {
	int x = 0, f = 1; char ch = getchar();
	while (!isdigit(ch)) {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (isdigit(ch)) {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}

const int maxn = 100005;
int n, k, tot;
int head[maxn], nxt[maxn<<2], to[maxn << 2], edge[maxn << 2];
int fa[maxn], dep[maxn], d[maxn];
bool vis[maxn];
int duan1, duan2, dis1, dis2;

void add(int u, int v, int w) { // 链式前向星
	to[++tot] = v;
	nxt[tot] = head[u];
	edge[tot] = w;
	head[u] = tot;
}

// 树的直径 dfs版 
void dfs(int u, int f, int w, int time) {
	dep[u] = dep[f] + w;
	if (time == 2) fa[u] = f; // 第二次记得存储父亲
	for (int i = head[u]; i; i = nxt[i]) {
		int v = to[i], w = edge[i];
		if (v == f) continue;
		dfs(v, u, w, time);
	}
	if (dep[u] > dep[duan1]) duan1 = u;
}

void dp(int u, int f) { // 树的直径 dp 版 
	for (int i = head[u]; i; i = nxt[i]) {
		int v = to[i];
		if (v == f) continue;
		// 如果 2 个节点在环内，那么边权设为 -1
		if (vis[u] && vis[v]) edge[i] = -1;
		dp(v, u);
		dis2 = max(dis2, d[u] + d[v] + edge[i]);
		d[u] = max(d[u], d[v] + edge[i]);
	}
}

int main() {
	n = read(), k = read();
	for (int i = 1; i < n; i++) {
		int u = read(), v = read();
		// 边权初始为 1
		add(u, v, 1), add(v, u, 1);
	}
	dfs(1, 0, 0, 1);
	dfs(duan1, 0, 0, 2); // duan1 为直径的一个端点
	dis1 = dep[duan1]; // 树的直径
	if (k == 1) {
		printf("%d", 2 * (n - 1) - dis1 + 1);
		return 0;
	}
	// 从 duan1 开始，每次找父亲，就把整个直径的路径都标记好了
	for (int i = duan1; i; i = fa[i]) vis[i] = 1;
	dp(1, 0);
	printf("%d", n * 2 - dis1 - dis2);
	return 0;
}