群/环/域

研一的时候学过近世代数，几乎没学到什么，后续自学一遍还是半知半懂，总结在【近世代数】这里了，现在再次回顾提炼一下要点！

集合（set）

一个集合\(G\)表示一组数据
有限集合：\(G=\left\{ g_1,g_2,...,g_n\right\},|G|=n\)
无穷集合：\(G=\left\{ g_1,g_2,...,g_n\right\},|G|=\infty\)

比如：一个班的所有学生

半群（semi-group）

一个集合\(G\)，以及一个二元运算（.），满足：
封闭性：\(a \in G,b \in G,a.b \in G\)
结合律：\((a.b).c=a.(b.c)\)

自然数集\(N=\left\{0,1,2,...\right\}\)是一个加法半群、一个乘法半群

群（group）

一个集合\(G\)，以及一个二元运算（.），满足：
封闭性：\(a \in G,b \in G,a.b \in G\)
结合律：\((a.b).c=a.(b.c)\)
有单位元：\(\exists e,e.a=a.e=a\)
有逆元：\(\forall a\in G,\exists b \in G,a.b=b.a=e\)

比如整数集：
对于加法构成群（单位元：0，逆元：0）
对于乘法不能构成群（单位元：0，没有逆元）

有限群

（1）群\(G\)中有有限个元素就称为有限群，元素的个数叫做"阶"，记\(|G|\)
（2）群\(G\)，对于\(a,b\in G\)，\(ab\)的逆为\(b^{-1}a^{-1}\)
（3）若群\(G\)运算为乘法，则\(a^n=aa....a（n个）\)
（4）若群\(G\)运算为加法，则\(na=a+a+...+a（n个）\)

• 群\((Z,+)\)为整数集对于加法构成的整数加群，单位元为0：\((Z,+)={k.1|k\in Z}\)
• 群$(Z_m,+)是模m剩余类环 \(Z_m\)对于加法构成的模m剩余类群，零元为\(\overline{0}\)（零元就是满足任意元素与之相乘，结果还是零元）：

\[(Z_m,+)=(\overline{0},\overline{1},...,\overline{m-1})=(l.\overline{1}|l=0,1,...,m-1) \]

• \(Z_{10}*=(\overline{1},\overline{3},\overline{7},\overline{9})=(\overline{3}^i|i=1,2,3,4)\)（*表示去0）

上述的三个群，都可以用一个元素\(a\)代表：通过整数幂次（或整数倍）表示群中所有元素，可以用\(a\)代表这个群。

交换群（commutative group）

又叫做阿贝尔群或者加群，需要满足：
1、群
2、交换律:\(a.b=b.a\)

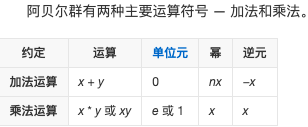
比如整数集上的加法群，也是一个交换群。

循环群（cyclic group）

设群\(G\)的运算记为乘法（或加法），如果\(G\)的每一个元素都能写成\(G\)中国某个元素\(a\)的整数幂次（或整数倍）的形式，则\(G\)叫做循环群，\(a\)是\(G\)的一个生成元，将\(G\)记做\(<a>\)
（1）设\(G=<a>\)，运算为乘法时，单位元为\(e\)
（2）当\(G\)是无限群时，\(\forall c\in N^+\)（\(N^+\)是正的自然数）都有\(a^n\neq e\)，此时

\[<a>={...,a^{-n},...,a^{-1},e,a^1,...,a^n,...} \]

此时G为无限循环群。上述整数加群\((Z,+)\)就是无限循环群。
（3）当\(G\)为有限群时，\(\exists n\in N^+\)，都有\(a^n=e\)，此时：\(<a>={e,a^1,..,a^{n-1}}\)
其群\(<a>\)的阶为n，上述\((Z_m,+)\)是m阶循环群，\(Z_{10}^*\)是4阶循环群。
（4）循环群一定是阿贝尔群，阿贝尔群不一定是循环群。

置换群（Permutation group）

所有的有限群都可以用置换群来表示。

有限集合Ω上的一些置换组成的集合，在置换的乘法下所组成的群，称为置换群。

置换：
有限集合到自身的一一映射称为一个置换。
例：\((a_1,a_2,a_3)->(a_2,a_1,a_3)\)

？

性质

同余关系

一个群\(G\),有一个二元运算(.),定义一个等价关系\(R\):
若等价关系满足：\(\forall a,b,c,d \in G,a R b, c R d : a.b R b.c\)，则\(R\)和运算(.)同余。

环（ring）

对一个集合G是环，且有两个二元运算（+，.），需满足：
1、对于加法运算，是一个交换群（封闭、结合律、单位元、逆元、交换律）
2、对与乘法运算，是一个半群（封闭、结合律）
3、满足分配律：\(\forall, a \in G,b \in G,c \in G,a.(b+c)=a.b+a.c\)

\(Z\)是整数环、\(R\)是实数环

交换环（commutative ring）

一个环\(G\)，其乘法运算满足交换律，即\(a.b=b.a\)

子环（sub ring）

G是一个环，R是G的一个非空子集，且满足：\(\forall a,b \in R,a+b \in R,a.b \in R\)，则R是G的一个子环。

理想环（ideal）

理想就是满足一定条件的子环，条件：
1、对于任意环\((G,+,.)\)，\(I\)叫做G的左理想，当满足：\(I\)是G的一个子环，且满足\(\forall r \in G,\forall x \in I,rx \in G\)
2、对于任意环\((G,+,.)\)，\(I\)叫做G的左右理想，当满足：\(I\)是G的一个子环，且满足\(\forall r \in G,\forall x \in I,xr \in G\)
故，若\(I\)既是左理想又是右理想，\(I\)是G的双边理想，即理想！

比如：偶数是整数的一个理想，偶数本身是整数的一个子集，既是左理想又是右理想。

商环（quotient ring）

理想的用途就是构造商环的
设\(I\)是环\(G\)的一个理想，定义\(G\)上的等价关系\(\sim\):

\[a \sim b : a-b \in I \]

\(\sim\)对于\(G\)上的加法和乘法运算是同余关系

至于什么是等价关系、等价类？，请参考：近世代数

由\(I\)能构造任意元素\(a \in G\)的等价类：\([a]=a+I:=\left\{a+r:r\in I \right\}\)，也可以写作\(a mod I\)
所有这些等价类构成一个商环，记\(G/I\)

例如：整数环\(Z\)的理想：偶数环\(2Z\)，则可以构造两个等价类

\[[0]=\left\{...,-2,0,2,... \right\} \]

\[[1]=\left\{...,-3,1,3,... \right\} \]

多项式环（polynomial ring ）

对于任意的一个环\(G\)，定义集合：

\[G[x]=\left\{a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0|a_i\in G,i=0,1,2,...,n \right\} \]

该集合是一个环，叫多项式环，n是多项式环的次数。

更多的关于多项式环的介绍，在后续介绍！

剩余类环（ring of residue classes）

模m的剩余类环

域（field）

定义：
对于一个集合\(G\)，有两个二元运算(+,.)，需要有：
1、加法和乘法满足结合律：\((a+b)+c=a+(b+c),(a.b).c=a.(b.c)\)
2、加法和乘法满足交换律：\(a+b=b+a,a.b=b.a\)
3、加法和乘法有单位元：a+0=0+a=a,a.1=1.a=a\( 4、加法和乘法**有逆元**：a+(-a)=(-a)+a=0,a.a^{-1}=a^{-1}.a=1\)
5、满足分配律：\(a.(b+c)=a.b+a.c\)

简单点说，"域"是一种可以进行加、减、乘、除（逆元）运算而结果不会超过自身的集合，可以看出，域就是环的一种，不同之处是域要求它的元素可进行除法运算，即每个非零元素都有【乘法逆元】，且域中元素关于乘法是可交换的【交换律】，即域是乘法可交换的除环。

更常见的是"数域"：
如果一个包含0，1在内的数集P，对于加、减、乘、除（除数不为0）是封闭的，则P是一个数域

常见的数域：复数域C；实数域；有理数域Q（自然数集N和整数集Z都不是数域，因为除法运算不是封闭的）

有限域（galois field，伽罗华域）

1、是一个数域
2、元素个数是有限个

性质

（1）有限域中元素的个数叫做"阶"，阶一定是素数的幂。
证明：
阶表示为\(p^n\)（p是素数，n是正整数），p就是有限域的"特征数"，通常用\(GF(p^n)\)表示\(p^n\)元的有限域

（2）元素个数相同的有限域是同构的

有限域上的多项式运算

这里以\(GF(2^8)\)域为例：p=2，n=8；给定多项式$f(x)=x^6 + x^4 + x^2+x+1 $，具有以下性质：
（1）多项式的系数只能是0和1，即[0,2-1]，若p=3，则系数可以取0，1，2；
（2）合并同类项【加法】，对系数进行异或，如 \(x^4 + x^4=0\)；
（3）减法就是加法，加上其负系数。如$x^4 – x^4 = x^4 + x^4 $

举例：
设\(f(x)=x^6 + x^4 + x^2+x+1\)，\(g(x)=x^7 + x+1\)
（1）加法

\[f(x)+g(x)=x^7+x^6+x^4+x^2+(1+1)x+(1+1)1=x^7+x^6+x^4+x^2 \]

（2）减法

\[f(x)–g(x)=f(x)+g(x)=x^7+x^6+x^4+x^2 \]

（3）乘法

\[f(x)*g(x)=(x^{13}+x^{11}+x^9+x^8+x^7)+(x^7+x^5+x^3+x^2+x)+(x^6+x^4+x^2+x+1)=x^{13}+x^{11}+x^9+x^8+x^6+x^5+x^4+x^3+1 \]

（4）除法

\[g(x)/f(x)=x 余 x^5+x^3+x^2+x+1 \]

另外有限域中的元素可以通过该域上的本原多项式生成，通过本原多项式得到的域，其加法单位元是0，乘法单位元是1
以\(GF(2^3)\)为例，指数小于3的多项式有8个：$$0，1，x，x+1，x^2 ，x^2 +1，x^2 +x，x^2 + x+1$$，其系数刚好是000,001,010,011,100,101,110,111，是0～7这8个数的二进制形式

素数域

在密码学中，最常见的是，n=1时，阶为p的素数域\(GF(p)\)或者阶为\(2^n\)的\(GF(2^n)\)域，当n=1时，\(GF(2)\)是二元域.

性质

（1）有限域\(GF(p^n)\)有\(p^n\)个元素，这里p是有限域的特征，n是有限域在其素域\(GF(p)\)上的次数。
（2）\(GF(p)\)就是mod p，元素在[0,p-1]之间
（3）p为什么是素数？
当p为素数时，才能保证集合中的所有元素都有加法和乘法逆元（0除外）。若p=10，虽然所有元素有加法逆元，但没有乘法逆元（比如2），若p为素数，才能保证域内所有元素都有逆元。

扩域（extension field）

如果L是K的一个字域，则K就是L的扩域，叫做L的域扩张，记K/L
复数域\(C\)是实数域\(R\)的扩域，而\(R\)则是有理数域\(Q\)的扩域

参考

1、群环域，理想商环，原根复习
2、抽象代数|笔记整理（6）——环，多项式环，理想
3、数域、有限域（伽罗瓦域）
4、近世代数(2)——循环群
5、群论(3): 置换群