【福建集训】单调队列（1/3）

A.气象台

首先想到把这个转化为区间问题，开始分类讨论

 

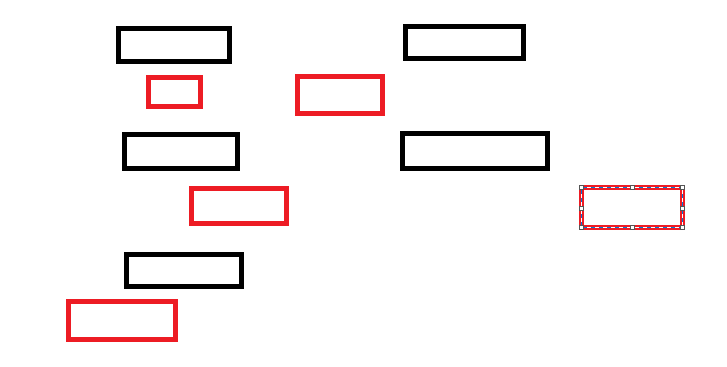
总共五种情况，会发现只有右上角那种不合法，如果令红色区间为i，黑色区间为j，j<i的话，有结论

Lj<=Ri时才合法

显然我们应该维护一个l的单调队列，但应该是单调递增还是单调递减嘞。

如果是单调递增：

显然对于这条结论我们会让一些元素从队尾剔除

但是这样就维护不了单调性了

所以应该是单调递减，特别的应该是单调不上升：

所以这个时候这条结论帮助我们剔除队首元素，队尾元素依赖单调性剔除

#include<bits/stdc++.h>
using namespace std;
#define re register

#define fo1(l,r) for(re int i=l;i<=r;++i)

#define fo2(l,r) for(re int j=l;j<=r;++j)

#define fo3(l,r) for(re int k=l;k<=r;++k)

#define fo4(l,r) for(re int tt=l;tt<=r;++tt)

#define fo(l) for(re int i=h[l],go;i;i=x[i].last)

#define inf 0x3f3f3f3f

#define INF 0x7fffffffffffffff

#define LL long long

#define itn int

#define DB double

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<3)+(x<<1)+ch-48;
        ch=getchar();
    }
    return x*f;
}
const int N=1e6+10;
int ll[N],rr[N],q[N],ANS;
inline int max2(itn xx,int yy)
{
    return xx>yy?xx:yy;
}
int main()
{
    freopen("tem.in","r",stdin);
    freopen("tem.out","w",stdout);
    int n=read();
    fo1(1,n)
    {
        ll[i]=read();
        rr[i]=read();
    }
    int h=1,r=1,now=1;
    fo1(1,n)
    {
        while(1)
        {
            if(r==h)
            {
                break;
            }
            if(ll[q[r-1]]>=ll[i])
            {
                break;
            }
            --r;
        }
        q[r]=i;++r;
        while(1)
        {
            if(ll[q[h]]<=rr[i])
            {
                break;
            }
            if(q[h]==now)
            {
                ++h;
            }
            ++now;
        }
        ANS=max2(ANS,i-now+1);
    }
    printf("%d",ANS);
    fclose(stdin);
    fclose(stdout);
    return 0;
}