Armijo-Goldstein准则的形象理解

Armijo-Goldstein准则是梯度下降法中选择步长的方法。我们知道，函数下降速度最快的方向为梯度方向,我们取出函数沿梯度方向的一个切面，做出函数值与步长的图像\(\phi(h)\).

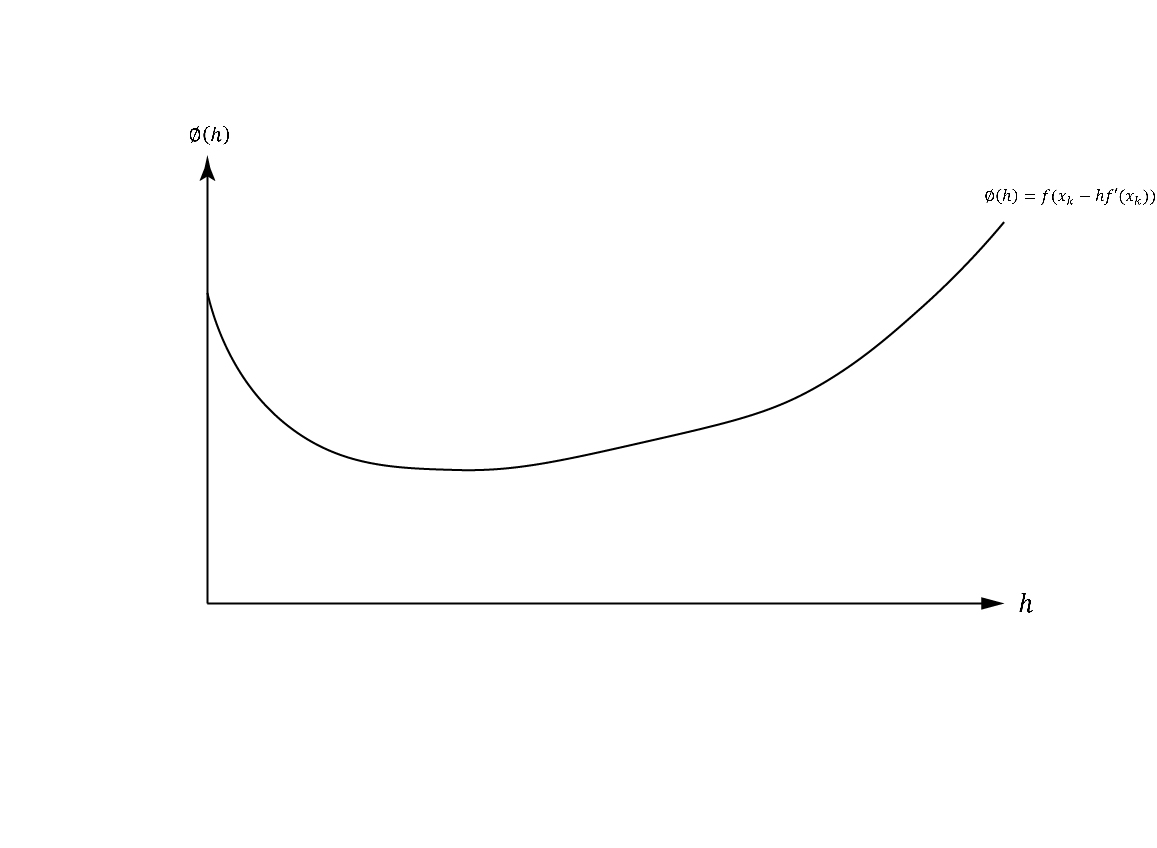
我们要选一点\(x_{k+1} = x_k - h f'(x_k)\), 使得目标函数逐渐下降。直觉来看，为了达到收敛到梯度为0点（极值点或驻点）的目的，需要满足：

1. \(f(x_{k+1})<f(x_k)\)，即函数值需呈下降趋势
2. \(x_{k+1}\)不能距离\(x_k\)过于近，即步长h不能过小

接下来我们通过下面人工做直线的方式，确定一个区间\([h_A,h_B]\)。使得从该区间中取任意值做步长计算\(x_{k+1}\)，都满足上述要求。具体来说，我们从点\((0, f(x_k))\)处“斜向下”做两条直线，交图像于A，B两点。我们希望能从\([h_A,h_B]\)范围内选一值计算\(x_{k+1}\)，满足上述要求1，2。

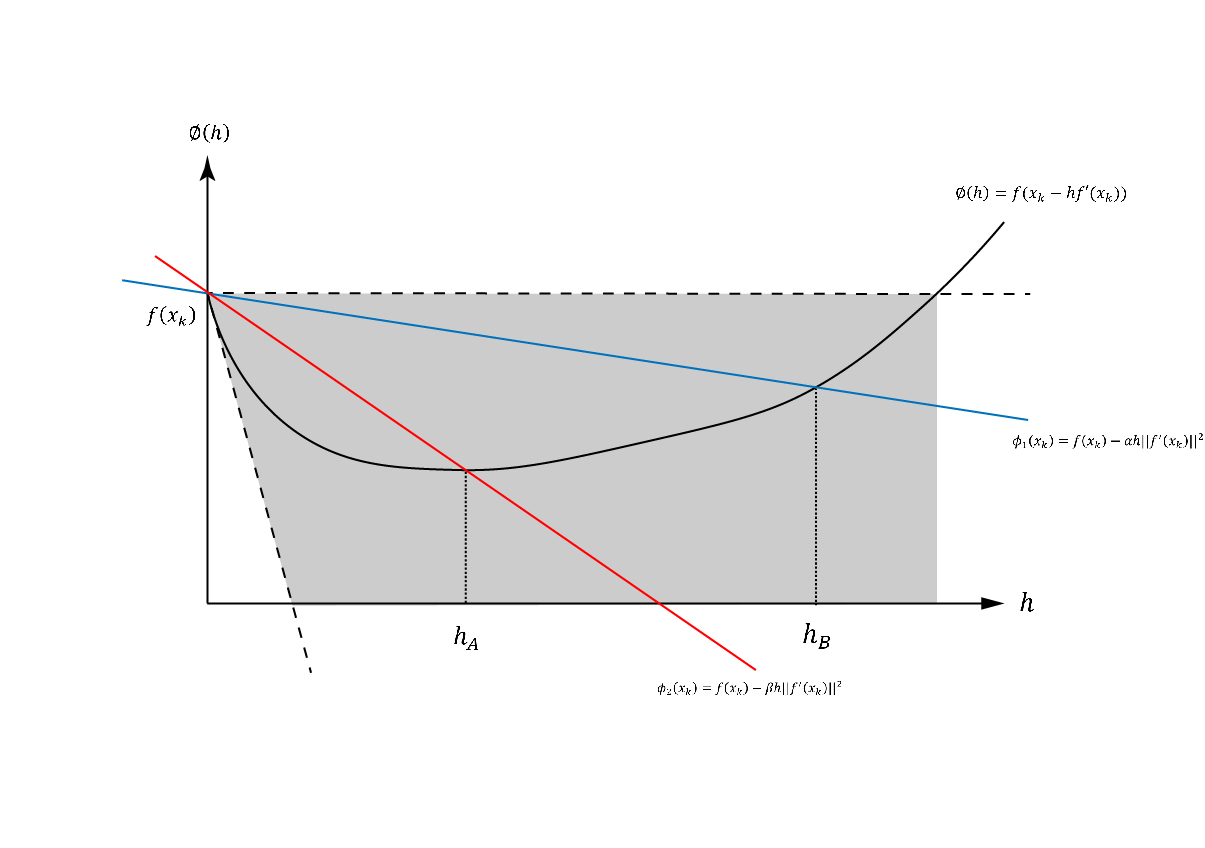
可以想象，若满足要求1，2，这两条直线需要停留在虚线所示的阴影区间中，不能太高，超过水平线，不能太低，小于切线斜率。也就是在h=0处，需要满足：

\[\phi(0) = \phi_2(0) = \phi_1(0), \phi'(0) < \phi_2'(0) < \phi_1'(0) < 0 \]

注意在\(h=0\)处，\(\phi'(0)=-\left\|f'(x)\right\|^2\). 于是我们人为构造如下两条直线，分别为：

\[\phi_1(h)=f(x_k)-\alpha h\left\|f'(x_k)\right\|^2 （图中蓝色直线） \]

\[\phi_2(h)=f(x_k)-\beta h\left\|f'(x_k)\right\|^2 （图中红色直线） \]

其中\(0<\alpha<\beta<1\)。易知这两条直线满足上述要求。
即红蓝两条直线截出的弧，满足要求（1）（2），不会太高，不会太低，刚刚好能够保证下一个取值的正确性。

注意在弧线处，根据函数图像我们有：

\[\phi_1(h) \le \phi (h) \le \phi_2(h) \]

也就是：

\[f(x_k)-\beta h\left\|f'(x_k)\right\|^2 \le f(x_k-hf'(x_k)) \le f(x_k)-\alpha h\left\|f'(x_k)\right\|^2 \]

注意我们有：

\[hf'(x_k)=x_k-x_{k+1} \]

代入上式即可导出:

\[\alpha\left<f'(x_k),x_k-x_{k+1}\right> \le f(x_k) -f(x_{k+1}) \]

\[\beta\left<f('x_k),x_k-x_{k+1}\right> \ge f(x_k) -f(x_{k+1}) \]

上式即Armijo-Goldstein规则的要求。
在有些材料表达当中，引入了梯度方向向量\(d_k\)，但整体思路是一致的，在此不再叙述。