树、二叉树、查找算法总结

1. 思维导图

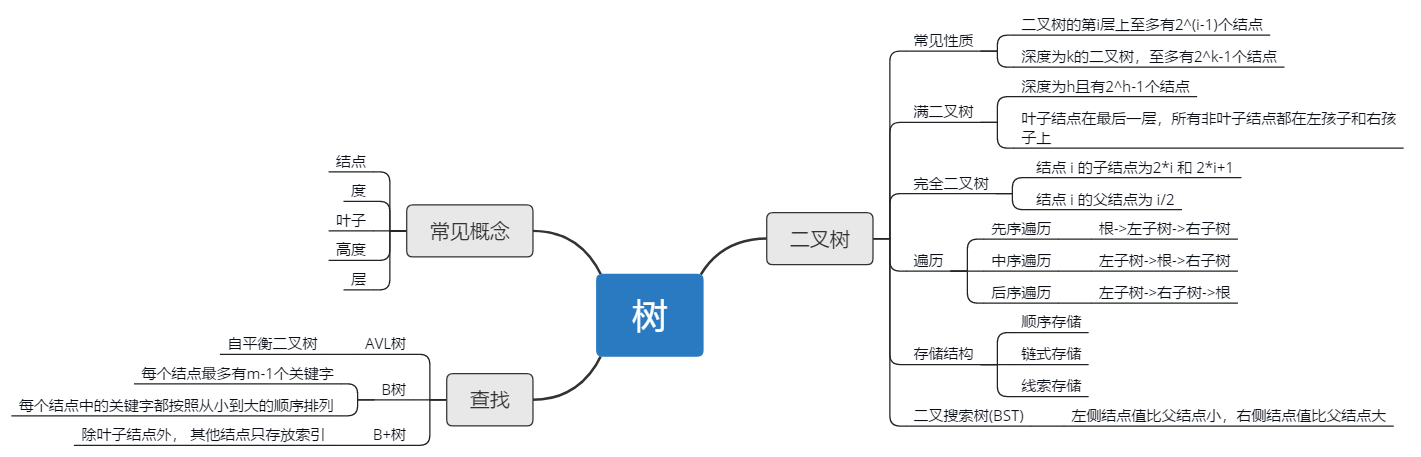
2. 概念笔记

1. 哈夫曼树

路径长度：树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目为路径长度。
树的路径长度：从根结点到每一个结点的路径长度之和。
权：若将树中结点赋一个有某种含义的数值，则这个数值称为该结点的权。
结点的带权路径长度：从根结点到该结点间的路径长度与该结点的权的乘积。
树的带权路径长度WPL：树中所有带权结点的路径长度之和。

构建：
1. 在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和。
2. 在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推。
3. 重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。

2. AVL树（网上找的图）

向右旋LL：由于在a的左子树根结点的左子树上插入结点，a的平衡因子由1增至2，需进行一次右旋转操作。

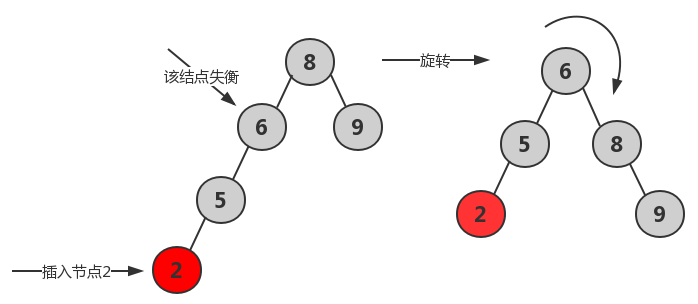
向左旋RR：由于在a的右子树根结点的右子树上插入结点，a的平衡因子由-1变为-2，需进行一次左旋转操作。

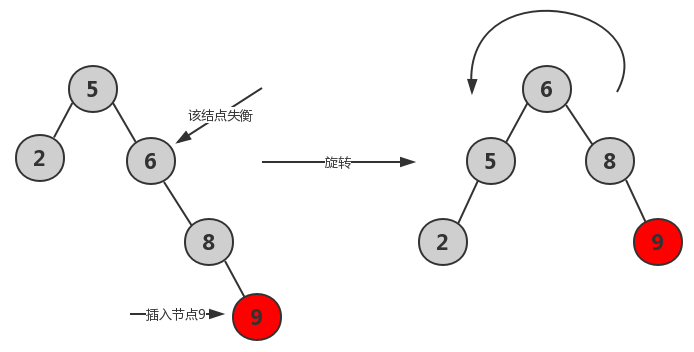
先左后右LR：由于在a的左子树根结点的右子树上插入结点，a的平衡因子由1增至2，需进行先左旋后右旋操作。

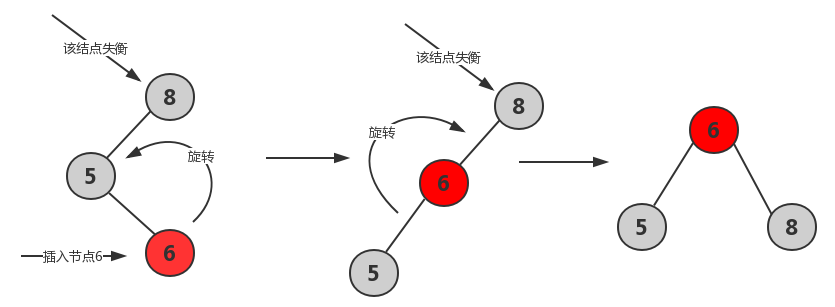
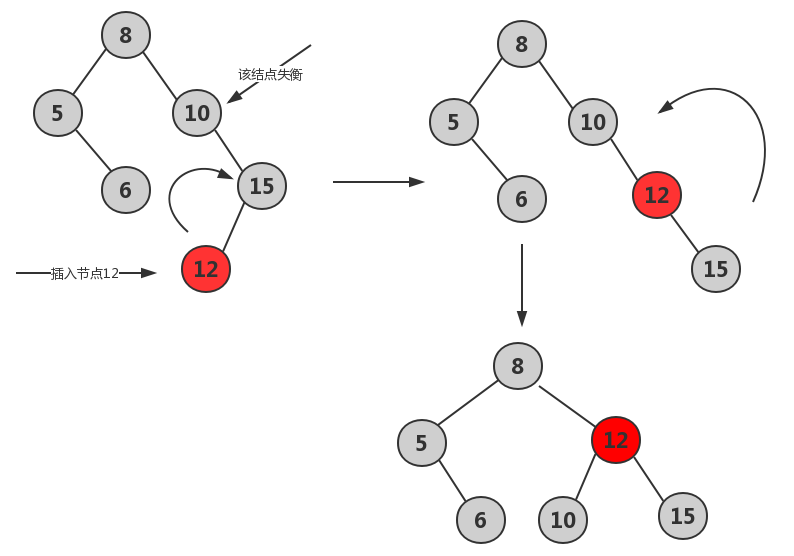
先右后左RL：由于在a的右子树根结点的左子树上插入结点，a的平衡因子由-1变为-2，需进行先右旋后左旋操作。

3. B树

• B树中所有节点的孩子节点数中的最大值称为B树的阶，记为M。
• 树中的每个节点至多有M棵子树。
• 若根节点不是终端节点，则至少有两棵子树。
• 除根节点和叶节点外，所有点至少有m/2棵子树。
• 所有的叶子结点都位于同一层。