算法入门--图及树的存储方式

α. 图的定义

在数据结构层面上，图是有两个集合组成（V ，E），V指的是顶点的集合，E指的是边的集合（V中顶点偶对的有穷集合）

β. 基本术语

术语	定义
顶点	V中的元素
有向图	有方向的图
无向图	没有指定方向的图
回路	存在第一个顶点和最后一个顶点的路径
完全图	图具有n个顶点且具有n*(n-1)/2 个边
稀疏图	边的数目比较少的图
稠密图	边的数目比较多的图
权	边的权值（未指定一般为一，具体情况具体分析）

γ. 图的分类

γ1. 有向图与无向图

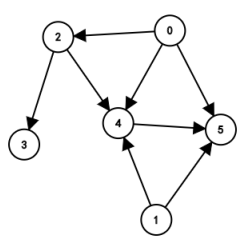
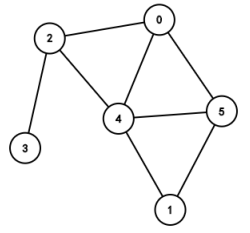
图1为有向图 2->4 指定了可以从2到4，但不可以从4 -> 2
图2，3，4为无向图 既可以从 2->4 又可以从 4->2

γ2. 稠密图与稀疏图

我们可以称图三为稀疏图，图四为稠密图，二者区分准则：边的条数|E|是否远小于|V|²，但这个概念是比较模糊的，官方也没有明确的定义，一般认为点的个数小于n*log2n(n对二取对数）

δ. 两种存储方法（C++实现）

δ1.邻接矩阵（适用于稠密图）

首先我们定义一个整数类型的二维矩阵，矩阵元素（a[3][4]) 的下标表示两一个顶点(3 和 4)，而a[3][4] 里面存储的数据便是顶点3 和 顶点4之间的距离，如果两个顶点相同,则里面存储的数据为0.

const int maxN = 1e3+10;
int g[maxN][maxN];

当然还会出现两个顶点不联通的情况，我们认为它们之间的距离为无穷大，但是我们肯定没法找出来一个无穷大的数，我们可以认为一般情况下，我们处理的数据不会很大，只要选取一个很大的数，相比较而言，那个很大的数就是无穷大了.

#define inf 0x3f3f3f3f

我们一般选取 0x3f3f3f3f 作为无穷大，0x3f3f3f3f的十进制是1061109567，也就是10^9级别的，而我们一般处理的边的长度也就几百几十，我们可以认为它是无穷大.

δ2.邻接表（适用于稀疏图）

首先我们维护一个vector数组(没有接触过vector的小伙伴可以点击进行学习)，数组的下标表示一个顶点，而每一个数组元素（如 v[3] ）里存储着与本顶点相连的点以及二者之间的距离.

const int maxN = 1e3+10;
vector<node>v[maxN];

但如何让每一个顶点的vector里的元素存储两个数据呢，这就用到了结构体，我们定义一个包含两个数据的结构体（相邻顶点以及之间的距离）

struct node{
    int e;int w;
    node(int e,int w){
        this->e = e;
        this->w = w;
    }
};

对于不相连的顶点不会记录到vector中，无需考虑不联通的顶点情况

δ3.实战演练

这里我们将以蓝桥杯(无向图存储)的一道题为例为大家讲解两种方法的用法先不讲解题哦~

很久以前，T王国空前繁荣。为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J是T国重要大臣，他巡查于各大城市之间，体察民情。所以，从一个城市马不停蹄地到另一个城市成了J最常做的事情。他有一个钱袋，用于存放往来城市间的路费。

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数），他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23。

J大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式
输入的第一行包含一个整数n，表示包括首都在内的T王国的城市数

城市从1开始依次编号，1号城市为首都。

接下来n-1行，描述T国的高速路（T国的高速路一定是n-1条）

每行三个整数Pi, Qi, Di，表示城市Pi和城市Qi之间有一条高速路，长度为Di千米。

输出格式
输出一个整数，表示大臣J最多花费的路费是多少。

样例输入1
5
1 2 2
1 3 1
2 4 5
2 5 4
样例输出1
135

题目很啰嗦，但我们要习惯，以后接触的题目有很多是这种，从中快速提取我们所需要的信息也是一种能力哦~

δ3.1 邻接矩阵

#include "bits/stdc++.h"
using namespace std;
#define inf 0x3f3f3f3f
const int maxN = 1e3+10;
int g[maxN][maxN];
int m,a,b,w;
void Init(){
    for(int i = 1;i <= m;i++){
        for (int j = 1; j <= m; ++j) {
            if(i == j){
                g[i][j] = 0;
            }else{
                g[i][j] = inf;
            }
        }
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>m;
    Init();
    for(int i = 1;i < m;i++){
        cin>>a>>b>>w;
        g[a][b] = w;
        g[b][a] = w;
    }
    for(int i =1;i <= m;i++){
        for (int j = 1; j <= m; ++j) {
            printf("%d ",g[i][j]);
        }
        printf("\n");
    }
    return 0;
}

δ3.2 邻接表

#include "bits/stdc++.h"
using namespace std;
#define inf 0x3f3f3f3f
const int maxN = 1e3+10;
struct node{
    int x;
    int v;
    node(int x,int v){
        this->x = x;
        this->v = v;
    }
};
vector<node>v[maxN];
int N,M,a,b,c;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>M;
    for (int i = 1; i < M; ++i) {
        cin>>a>>b>>c;
        v[a].push_back(node(b,c));
        v[b].push_back(node(a,c));
    }
    for (int i = 1; i <= M; ++i) {
        printf("%d",i);
        for (int j = 0; j < v[i].size(); ++j) {
            printf("-> (%d %d)",v[i][j].x,v[i][j].v);
        }
        printf("\n");
    }
    return 0;
}

树其实是一种特殊的图，因此在存储的时候所使用的方法和图一样的~