Python Scipy库入门这一篇就行了
scipy cluster
用于聚类分析,比如K-Means
from numpy import vstack, array
from numpy.random import rand
from scipy.cluster.vq import whiten, kmeans, vq
data = vstack((rand(100, 3) + array([.5, .5, .5]), rand(100, 3)))
# 白化数据
data = whiten(data)
# 指定簇集的个数,获得簇中心
centroids, _ = kmeans(data, 3)
# 根据指定的簇中心对数据进行聚类
clx, _ = vq(data, centroids)
print(clx)
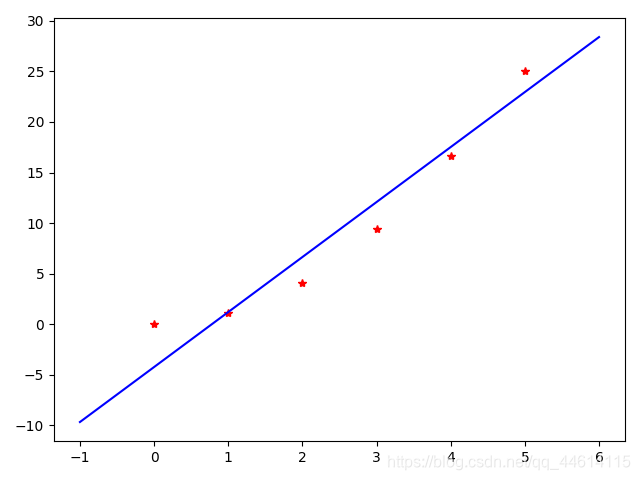
scipy.odr
用于回归分析
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i ** 2 + random.random() for i in x])
def linear_func(p, x):
m, c = p
return m * x + c
linear_model = Model(linear_func)
data = RealData(x, y)
odr = ODR(data, linear_model, beta0=[0., 1.])
out = odr.run()
out.pprint()
beta = out.beta
x_track = np.linspace(-1, 6, 100)
y_track = beta[0] * x_track + beta[1]
plt.plot(x, y, 'r*', x_track, y_track, 'b-')
plt.show()
scipy.stats
用于统计分析
生成服从指定分布的随机数
stats.norm.rvs(loc ,scale ,size )
loc:正态分布的期望
scale:正态分布的标准差
size:指定随机数的形状参数
# 生成服从于正态分布的随机数
import numpy as np
import scipy.stats as st
random_array = st.norm.rvs(loc=0, scale=0.1, size=(5, 5))
print(random_array)
'''
[[ 0.08032507 0.04995535 -0.11339123 0.04988461 -0.00184663]
[-0.06463444 -0.16271425 -0.05429032 -0.05717832 0.14683614]
[ 0.07611145 -0.07284285 -0.06833373 -0.05064769 0.16348252]
[ 0.0632136 0.25100341 -0.04703659 -0.11957341 0.00846529]
[ 0.050868 0.10585317 0.01720439 0.07208371 -0.00230902]]
'''
求概率密度函数指定点的函数值
stats.norm.pdf(point, loc, scale)
point: 点
loc: 正态分布的标准差
scale:正态分布的期望
import numpy as np
import scipy.stats as st
norm_res = st.norm.pdf([0, 1, 2], loc=0, scale=1)
print(norm_res)
'''
[0.39894228 0.24197072 0.05399097]
'''
求累计分布函数指定点的函数值
stats.norm.cdf(point, loc, scale)
point:点
loc: 正态分布的标准差
scale:正态分布的期望
import numpy as np
import scipy.stats as st
res = st.norm.cdf(0, loc=0, scale=1)
print(res)
'''
0.5
'''
scipy.special
提供数学函数,这里给出不常见的函数
| 函数名 | 描述 |
|---|---|
| comb(N,M) | 组合数 |
| perm(N,M) | 排列数 |
| beta(a,b) | beta函数 |
scipy.linalg
用于矩阵求解运算
下面求解本线性方程组
x
1
+
4
∗
x
2
+
2
∗
x
3
=
7
4
∗
x
1
+
2
∗
x
2
+
6
∗
x
3
=
23
8
∗
x
1
+
23
∗
x
2
+
5
∗
x
3
=
5
x1 + 4*x2 + 2*x3 = 7\\ 4*x1 + 2*x2+6*x3 = 23\\ 8*x1+23*x2+5*x3 = 5
x1+4∗x2+2∗x3=74∗x1+2∗x2+6∗x3=238∗x1+23∗x2+5∗x3=5
from scipy import linalg as lg
import numpy as np
mat = [[1, 4, 2], [4, 2, 6], [8, 23, 5]]
res = [7, 23, 5]
# 求矩阵的行列式
print(lg.det(mat))
'''
136.0
'''
# 求矩阵的特征值
print(lg.eig(mat))
'''
(array([17.29893809+0.j, -0.94058671+0.j, -8.35835137+0.j]), array([[ 0.20841245, 0.85648921, 0.034842 ],
[ 0.40383822, -0.17223167, -0.51096382],
[ 0.89077435, -0.48658245, 0.85889581]]))
'''
# 求矩阵的逆矩阵
print(lg.inv(mat))
'''
[[-0.94117647 0.19117647 0.14705882]
[ 0.20588235 -0.08088235 0.01470588]
[ 0.55882353 0.06617647 -0.10294118]]
'''
# 求解线性方程组
print(lg.solve(mat, res))
'''
[-1.45588235 -0.34558824 4.91911765]
'''
# 利用Numpy库求矩阵的秩
print(np.linalg.matrix_rank(mat))
'''
3
'''
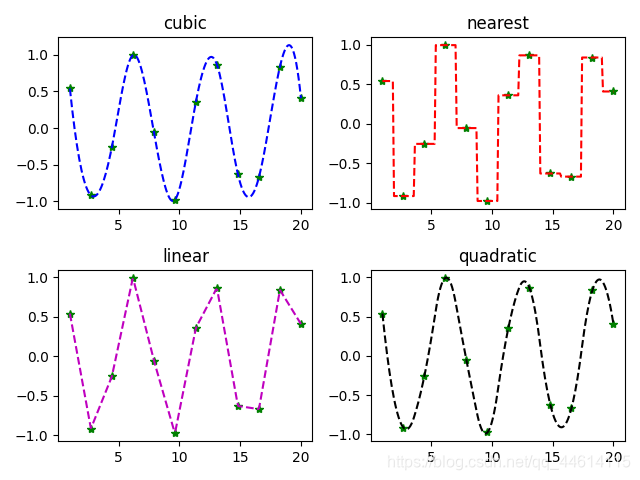
scipy.interpolate
用于插值计算
fun = interp1d(x, y, kind)
x: 横坐标
y:纵坐标
kind:差值方法
| kind | 描述 |
|---|---|
| nearest | 最邻近插值法 |
| zero | 阶梯插值 |
| slinear、linear | 线性插值 |
| quadratic、cubic | 2、3阶B样条曲线插值 |
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(1, 20, 12)
y = np.cos(x)
f1 = interp1d(x, y, kind='cubic')
f2 = interp1d(x, y, kind='nearest')
f3 = interp1d(x, y, kind='linear')
f4 = interp1d(x, y, kind='quadratic')
x_index = np.linspace(1, 20, 200)
y_index = f1(x_index)
plt.subplot(2, 2, 1)
plt.title('cubic')
plt.plot(x, y, 'g*')
plt.plot(x_index, y_index, 'b--')
x_index = np.linspace(1, 20, 200)
y_index = f2(x_index)
plt.subplot(2, 2, 2)
plt.title('nearest')
plt.plot(x, y, 'g*')
plt.plot(x_index, y_index, 'r--')
x_index = np.linspace(1, 20, 200)
y_index = f3(x_index)
plt.subplot(2, 2, 3)
plt.title('linear')
plt.plot(x, y, 'g*')
plt.plot(x_index, y_index, 'm--')
x_index = np.linspace(1, 20, 200)
y_index = f4(x_index)
plt.subplot(2, 2, 4)
plt.title('quadratic')
plt.plot(x, y, 'g*')
plt.plot(x_index, y_index, 'k--')
plt.show()
scipy.integrate
用于计算多重积分
import numpy as np
from scipy.integrate import tplquad, dblquad, quad
# 返回结果和误差
val1, err1 = quad(lambda x: np.sin(x), 0, np.pi) # x上界pi
print('积分结果:', val1)
'''
积分结果: 2.0
'''
# 二重积分
val2, err2 = dblquad(lambda x, y: np.sin(x) * np.cos(y / 2), 0, 2, 4, 6)
print(val2)
'''
-2.7159551561049335
'''
# 三重积分
val3, err3 = tplquad(lambda z, y, x: np.sin(x) / np.sqrt(x + y ** 2) + np.cos(z ** 3), -3, 5, 2, 4, 3, 4)
print(val3)
'''
-1.2868508936407685
'''


 浙公网安备 33010602011771号
浙公网安备 33010602011771号