《浅谈格路计数相关问题》 - 学习笔记
ddy Orz
好像是一些很妙妙的东西,但是更妙妙的东西被略过了(
开始抄论文。
2 \(\text{Dyck}\) 路

2.3 \((n,m)\!-\!\text{Dyck}\) 路的计数
很显然,如果 \(n\perp m\) ,那么有 \(period(P)=n+m\) 。
然后考虑把互为循环移位的一组 \(P\) 放在一起考虑,即一次考虑 \(n+m\) 个。
惊喜地发现,这 \(n+m\) 个里面好像恰好有一个是 \text{Dyck} 路,而其他都不是。
存在性:任取一条不合法路径出来(显然这个是一定存在的),找到所以 \(y={m\over n}x\) 下方的点,取出到这条直线距离最远的点。这个点会把路径分成 \(P_1P_2\) ,那么可以发现把路径重组成 \(P_2P_1\) 就一定合法了。
唯一性:如果拆出来的点不是距离最远的那么一定不合法。如果存在两个距离相等(且不为 0 )的点,那么经过这两个点的直线与 \(y={m\over n}x\) 平行,而这与 \(n\perp m\) 矛盾。
所以 \(n\perp m\) 时 \((n,m)\!-\!\text{Dyck}\) 路的数量为 \({1\over n+m}{n+m\choose n}\) 。
2.4 有 \(k\) 个峰的 \((n,m)\!-\!\text{Dyck}\) 路计数
定义峰为路径中连续两步为 \(UL\) 的个数。
考虑把路径里的连续 \(U\) 和连续 \(L\) 缩成一个,那么路径会长成 (L)ULULUL..UL(U) 的样子。用插板法容易得到有 \(k\) 个峰的 \((0,0)\) 到 \((n,m)\) 的自由路数量为 \({n\choose k}{m\choose k}\) 。
而如果还要求是 \((n,m)\!-\!\text{Dyck}\) 路呢?同样假设 \(n\perp m\) 。此时缩点之后的合法路径只能长成 ULULUL...UL 的样子,并且离直线距离最远的一定是 \(LU\) 之间那个点。这样的点有 \(k\) 个,所以可以得到数量为 \({1\over k}{n-1\choose k-1}{m-1\choose k-1}\) 。
2.5 \(t\!-\!\text{Dyck}\) 路计数

这里满足 \(t\) 为正整数。由于斜率变得任意,所以不能直接用翻折法了。
由于 \(\gcd(n,tn)=n\) ,所以不能照搬上面的做法。但是考虑到 \(\gcd(n,tn+1)=1\) ,所以可以看看把终点往上移一格会发生什么。
发现这样非常 amazing 啊,把得到的 \((n,tn+1)\!-\!\text{Dyck}\) 路的第一个 \(U\) (显然第一个只能是 \(U\) )删掉之后,竟然刚好能对应回一条 \((n,tn)\!-\!\text{Dyck}\) 路。
这是因为连接 \((0,0),(n,tn)\) 和连接 \((0,0),(n,tn+1)\) 的线段之间没有整点,而临界状态的那些点往下一格刚好也还是合法的。
所以 \(m=tn\) 的各种东西也可以数了。
甚至还有更有趣 (niubi) 的东西:

不是很懂这两条是否真的是对的:直接令 \(t={m\over n}\) , (12) 给出的答案是 \({1\over n+1}{n+m\choose n}\) ,但 \(n\perp m\) 时刚刚推出来的答案是 \({1\over n+m}{n+m\choose n}\) 。或许是笔误?
然而被略过了(
3 不相交格路
大力映射,大力翻折。
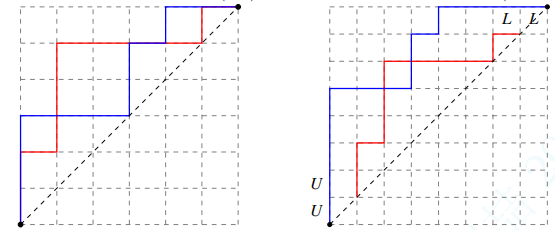
3.1 \(n\) 阶不交 \(\text{Dyck}\) 路计数

注意定义里写的是穿过,即重合是不算相交的。强制 \(P\) 在 \(Q\) 上方。什么时候会相交呢?某个时刻 \(P,Q\) 在同一个点,然后 \(Q\) 往上走, \(P\) 往右走,这就算穿过。
穿过的定义和 LGV 引理使用的条件略有不同,所以考虑修改一下。把 \(P\) 往左再往上移动一格,起终点变为 \((-1,1),(n-1,n+1)\) ,此时如果 \(P,Q\) 有公共点那么就认为它们相交。
现在应该已经可以使用 LGV 引理了(不相交路径的定义相同了,并且如果起终点反了那么一定会相交,所以不会被算进答案),但是形式还不够好看。
我们强行让路径 \(P\) 的开头向下延伸两格,结尾向右延伸两格,可以发现答案不变。此时所有起点终点都在 \(y=x\) 上,路径条数就是卡特兰数。运用 LGV 引理,得到答案 \(C_{n+2}C_n-C_{n+1}^2\) 。
然后又是更有趣 (niubi) 的东西:
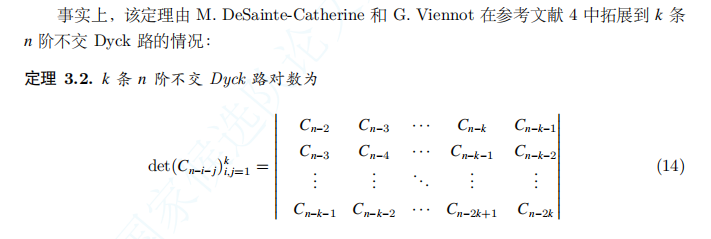
然后又被略过了(((
不过这个式子的下标好像和上面那个 \(C_{n+2}C_n-C_{n+1}^2\) 不太一样,大概是定义的锅。
这个式子看起来很像是用 LGV 引理求出来的东西。
3.2 不交自由路对计数

先考虑不接触自由路对。这个除了起点终点就很迷惑,所以考虑 \(P\) 的第一步必然是 \(U\) ,最后一步必然是 \(L\) , \(Q\) 同理。所以都删掉第一步和最后一步,得到 \((\tilde{P},\tilde Q)\) (即 \(P=U\tilde PL,Q=L\tilde QU\) )。现在 \(\tilde P,\tilde Q\) 完全没有公共点,直接应用 LGV 引理得到

再考虑不交自由路,其实一模一样,往左上平移一格即可。
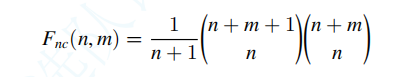
3.3 不接触自由路对与 \(k\) 个峰的 \(\text{Dyck}\) 路的关系
可以造出一个有趣的映射。
(我就是论文搬运工)


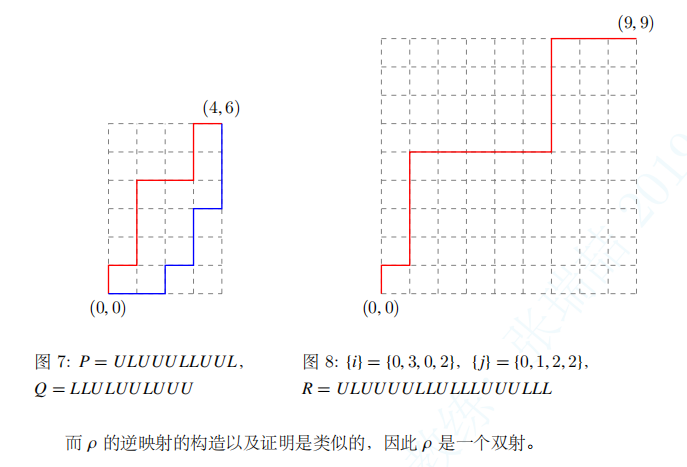
剩下的实际应用不想看了,就这样吧。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号