《一些特殊的数论函数求和问题》 - 学习笔记

orzzzzzzzt

边界条件的细节全部抄论文，希望没锅。其他内容也是全部抄论文。

复杂度分析方面基本全部略过了，放弃治疗，以后再说。

第一部分说了很多关于洲阁筛和 min25 筛的东西，并大力分析了一波复杂度，懒得细看了。

定义 \(big_i,small_i\) 分别为 \(i\) 的最大最小质因子， \(cnt_i\) 表示 \(i\) 的可重质因子个数。特别注意 \(i=1\) 时， \(big_i=small_i=\infty,cnt_i=0\) 。

素数的 \(k\) 次幂前缀和

显然可以 min25 筛做到 \(O({n^{3\over 4}\over \log n})\) ，但还可以更好。

我怀疑上面的 \(big_i\) 真正的意思应该是最小质因子。

考虑 \(\phi(x,a)\) ，当 \(x^{1\over 3}\le B=p_a\le x^{1\over 2}\) 时，可以枚举 \(x\) 有几个质因子，得到

\[\phi_{k}(x, a)=P_{0, k}(x, a)+P_{1, k}(x, a)+P_{2, k}(x, a)=1+\pi_{k}(x)-\pi_{k}\left(p_{a}\right)+P_{2, k}(x, a) \]

注意我们真正要算的是 \(\pi_k(x)\) ，所以移项可以得到

\[\pi_{k}(x)=\phi_{k}(x, a)+\pi_{k}\left(p_{a}\right)-P_{2, k}(x, a)-1 \]

由于 \(p_a\) 并不大，可以 \(O(B)\) 筛出来。所以考虑怎么求 \(\phi_{k}(x, a)\) 和 \(P_{2, k}(x, a)\) 。

3.1

事实证明 \(P_{2,k}(x,a)\) 更加容易计算。枚举 \(n=pq\) ，那么有 \(p_a<p\le q\le {x\over p}\) ，同时有 \(B<q<{x\over B}\) 。枚举 \(p\) ，计算所有 \(q\) 的贡献即可。复杂度 \(O({x\over B})\) 。

3.2

容斥一下，容易得到 \(\phi_k(x,a)=\phi_k(x,a-1)-p_a^k \phi_k(x/p_a,a-1)\) 。

根据这个容斥的过程推一推，可以得到

\[\phi_{k}(x, a)=\sum_{b i g_{n} \leq p_{a}, s m a l l_{n}>p_{b}} \mu(n) n^{k} \phi_{k}\left(\left\lfloor\frac{x}{n}\right\rfloor, b\right) \]

（这里的 \(big_n\) 又恢复为最大质因子了）

那么很容易得到 \(\phi_k(x,a)=\sum_{big_n\le p_a} \mu(n)n^k{\lfloor {x/n}\rfloor^k}\) 。

对于 \(n\le p_a=B\) 的 \(n\) 可以暴力统计。

然后我们有一个非常诡异的式子：

\[\sum_{n>B, b i g_{n} \leq p_{a}} \mu(n) n^{k}\left\lfloor\frac{x}{n}\right\rfloor^{k}=\sum_{B<n \leq B \times s m a l l_{n}} \mu(n) n^{k} \phi_{k}\left(\left\lfloor\frac{x}{n}\right\rfloor, \pi_{0}\left(s m a l l_{n}\right)-1\right) \]

这是什么意思呢？相当于是 dfs 从大到小枚举质数，做前面那个容斥，但做到 \(n>B\) 的时候就停止递归。注意 \(n\le B\times small_n\) 在 \(n\) 不是质数的时候隐含了 \(big_n\le B=p_a\) 的条件，所以我觉得应该还要加上 \(n\notin \text{prime}\) ？

令 \(p=small_n,m=n/p\) ，那么 \(\mu(m)=-\mu(n)\) ，所求即为

\[-\sum_{p \leq B }\sum_{small_{m}>p, m \leq B<m p} \mu(m) m^{k} p^{k} \phi_{k}\left(\left\lfloor\frac{x}{m p}\right\rfloor, \pi_{0}(p)-1\right) \]

然后继续阈值法。

3.2.1 \(p\le \sqrt B\)

此时 \(\pi_0(p)\) 是 \(O({\sqrt{B}\over \ln B})\) 级别， \(\lfloor\frac{x}{m p}\rfloor\) 也只有 \(O(\sqrt x)\) 种，所以可以直接用容斥方法把 \(\phi\) 的值全部求出来，然后无脑 \(O(B^{3\over 2})\) 枚举 \(p,m\) 求答案。由后文可知 \(B<\sqrt x\) ，所以复杂度瓶颈在求 \(\phi\) ，为 \(O({\sqrt{xB}\over \log B})\) 。

3.2.2 \(p>x^{1\over 3}\)

当 \(p>\sqrt B\) 时，如果 \(m\) 不为质数，则 \(m> p^2>B\) 不合法。所以只需要考虑 \(m\) 为质数的情况。同时显然有 \(pm>B\) 。求和式变为

\[\sum_{x^{1/3}<p \leq B }\sum_{p<q \leq B} (pq)^{k} \phi_{k}\left(\left\lfloor\frac{x}{pq}\right\rfloor, \pi_{0}(p)-1\right) \]

由于 \(p>x^{1\over 3}\) ，有 \(\lfloor {x\over pq}\rfloor <x^{1\over 3}<p\) ，所以根据定义有 \(\phi_{k}\left(\left\lfloor\frac{x}{pq}\right\rfloor, \pi_{0}(p)-1\right)=1\) 。

所以只需要暴力枚举 \(p\) ，求 \(q\) 的贡献，把素数 \(k\) 次方和筛出来即可。复杂度 \(O(B)\) 。

3.2.3 \({\sqrt B}<p\le x^{1\over 3}\)

此时求和式为

\[\sum_{\sqrt B<p\le x^{1/3} }\sum_{p<q \leq B} (pq)^{k} \phi_{k}\left(\left\lfloor\frac{x}{pq}\right\rfloor, \pi_{0}(p)-1\right) \]

直接用定义冲

\[\begin{align*} &\sum_{\sqrt{B}<p \leq x^{1/3}} \sum_{p<q \leq B}(p q)^{k} \phi_{k}\left(\left\lfloor\frac{x}{p q}\right\rfloor, \pi_{0}(p)-1\right) \\ =&\sum_{\sqrt{B}<p \leq x^{1/3}} \sum_{p<q \leq B}(p q)^{k} \sum_{p q r \leq x, s m a l l_{r} \geq p} r^{k}\\ =&\sum_{r=1}^{\left\lfloor x/B\right\rfloor} r^{k} \sum_{\sqrt{B}<p \leq x^{\frac{1}{3}}} \sum_{p<q \leq B}(p q)^{k}\left[p q r \leq x, small_{r} \geq p\right] \\ =&\sum_{r=1}^{\left\lfloor x/B\right\rfloor} r^{k} \sum_{\sqrt{B}<p \leq \min \left(x^{1/3}, small_{r}\right)} p^{k} \sum_{p<q \leq \min \left(\frac{x}{p r}, B\right)} q^{k} \end{align*} \]

我们可以枚举 \(p\) ，用树状数组维护 \(small_r\ge p\) 的 \(r\) ，再用数论分块枚举 \({x\over pr}\) 来获得 \(q\) 的贡献。需要在树状数组上查询 \(O(\sqrt{x/p})\) 次。下面分别分析树状数组修改和查询的复杂度。

修改的复杂度

一个神奇定理：对于任意 \(0<\alpha<1\) ， \(n\) 以内恰好有 \(k\ge 1\) 个质因子且最小质因子不小于 \(n^{\alpha}\) 的数的个数是 \(O\left({n\over {\log^k n}}\right)\) 的。证明使用神奇归纳法+神奇积分。

在这里我们不关心 \(r\) 有几个质因子，但确实需要 \(r\) 的最小质因子不小于 \(\sqrt B\) 才能造成贡献，所以有用的 \(r\) 只有 \(O\left({x/B\over {\log x}}\right)\) 个。乘上树状数组的复杂度，恰好 \(O(x/B)\) 。

（论文里面写这里的复杂度是 \(O(x^{2/3})\) ，不是很懂）

查询的复杂度

又是一个神奇定理： \(\sum_{p\le m}\sqrt{x\over p}=O\left({\sqrt{mx}\over {\log m}}\right)\) 。证明用神奇积分。

由于 \(p\le x^{1/3}\) ，代入 \(m=x^{1/3}\) 可知，询问次数是 \(O\left({x^{2/3}\over {\log x}}\right)\) 的。乘上一个 \(\log\) 恰好是 \(O(x^{2/3})\) 。

到这里已经分析完所有情况了，总复杂度为 \(O\left(x^{2/3}+{x\over B}+{\sqrt{xB}\over \log B}\right)\) ，取 \(B=x^{1\over 3}\log^{2\over 3}x\) ，则后半部分复杂度为 \(O\left(\left(\frac{x}{\log x}\right)^{2/3}\right)\) ，总复杂度仍为 \(O(x^{2/3})\) 。

3.3 优化

为了降低复杂度，必须进一步优化 \({\sqrt B}<p\le x^{1\over 3}\) 的部分。

可以考虑进一步利用那个定理。当 \(r\) 是质数时很容易统计贡献，而不是质数的 \(r\) 只有 \(O\left({x/B\over {\log^2 x}}\right)\) 个，乘一个 \(\log\) 也没有任何问题了。

而 \(r\) 不是质数时有 \(r>p^2\) ，并且为了有 \(q\) 存在需要 \(p<{x\over pr}\) ，于是得到 \(p\le x^{1/4}\) 。此时查询的复杂度降为 \(O\left(x^{5/8}\right)\) ，不会影响复杂度。

于是喜提复杂度 \(O\left(\left(\frac{x}{\log x}\right)^{2/3}\right)\) 。

3.4 总结

这个算法大概暂时只属于理性愉悦的范畴吧，反正我是不会去写的（

不过启发意义还是很大的，反正我每一步都想不到 /kk

第一步就非常魔幻，凭空造了一个阈值，并写了一个非常简单的式子，然后移项，突然就获得了一个思路。然后用 \(B^{1/2}\) 和 \(x^{1/3}\) 这两个阈值疯狂操作，拆成三个部分，各个击破。

\(B^{1/2}\) 这个阈值应该是为了让 \(m\) 变成质数而造出来的，而 \(x^{1/3}\) 是为了让 \(\phi_{k}\left(\left\lfloor\frac{x}{pq}\right\rfloor, \pi_{0}(p)-1\right)=1\) 。

由于质数的优秀性质，以及 \(pq\ge \min(p,q)^2\) ，把质数和合数分开讨论来得到更优秀的复杂度。

还要记住各种结论

约数函数前缀和

给定 \(n<2^{63}\) ，求 \(\sum_{i=1}^n \sigma(i)\) 。

Stern-Brocot Tree 和 Farey neighbour

具体数学里面应该有。

4.4 初步思路

转化统计 \(xy=n\) 下方的整点个数。

4.5 利用Stern-Brocot Tree切割曲线

（这一节对于做题可能不是特别必要，因为有更好看且优美的做法）

相当于是每次用一条直线拟合图像，统计直线下方的点数，然后递归做两边。

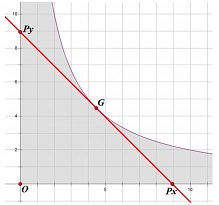
找到这么一条直线之后统计直线下方的点数是容易的，然后可以迭代计算两边的整点数。

4.5.1 坐标系转换

怎么计算 \(S(x_0,y_0,a,b,c,d)\) 呢？以 \(P\) 为原点， \(PR,PQ\) 分别为 \(u,v\) 轴，建立新的平面直角坐标系。在这个坐标系中，往轴的方向走一步，相当于是走到下一个接触的整点。

由于 \(\gcd(a,b)=\gcd(c,d)=1\) ，对于 \((u,v)\) ，可以得到它在原坐标系中的坐标

\[x=x_0+ud-vb\\ y=y_0-uc+va \]

同时由这两个式子也可以推出原坐标系中的整点 \((x,y)\) 在新坐标系中的坐标。两式分别乘 \(a,b\) 相加，得到

\[ax+by=ax_0+by_0+(ad-bc)u \]

由于 \({a\over b},{c\over d}\) 是 Farey neighbour ，所以有 \(ad-bc=1\) ，于是 \(u\) 是整数；同理 \(v\) 也是整数。

因此，原坐标系中的整点和新坐标系中的整点一一对应。

\(xy=n\) 对应成什么了呢？令 \(w_1=ax_0+by_0,w_2=cx_0+dy_0\) ，那么有 \(H(u,v):(u+w_1)(v+w_2)-cd(u+w_1)^2-ab(v+w_2)^2=n\) 。

由于 \(w_1,w_2,ab,cd\ge 0\) ，所以在这个曲线上任意 \(u>0\) 唯一对应一个 \(v\) ，反之亦然。设 \(v=V(u),u=U(v)\) ，那么 \(U,V\) 在第一象限中均为凹函数，性质与 \(xy=n\) 类似。

（以上基本上抄论文）

4.5.2 利用坐标系的转换统计整点数

现在，在新的坐标系里面，找到斜率为 -1 的切线，统计切线下方的整点数。设切点为 \(G\) ，它的 \(u,v,x,y\) 坐标分别为 \(G_u,G_v,G_x,G_y\) 。

然后找到另外两个整点 \(S,T\) ，满足

\[S_u\le G_u<S_u+1=T_u\\ S_v=\lfloor V(S_u)\rfloor\\ T_v=\lfloor V(T_u)\rfloor \]

感性理解，就是在曲线下方、 \(G\) 两边，找到恰好夹住 \(G\) 的两个整点。

过 \(S,T\) 分别作切线的平行线， \(SA\) 交 \(v\) 轴于 \(A\) ， \(TB\) 交 \(u\) 轴于 \(B\) 。 \(A\) 往上一格是 \(M\) ， \(M\) 作平行线交曲线于 \(N\) ； \(B\) 往右一格是 \(C\) 。

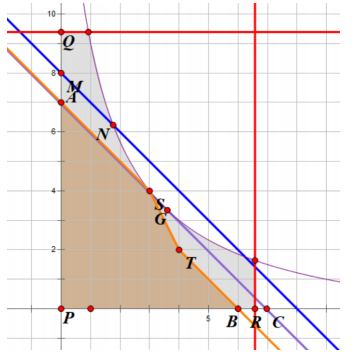
（我其实不是很懂为什么在这个图中， \(Q\) 和 \(R\) 怎么就不在曲线上了）

然后把折线 \(A-S-T-B\) 下方（也就是橙色线条和橙色阴影）的整点统计进答案。

那么我们断言，当前未被统计的， \(PG\) 上方的点，就是 \(MN\) 上方（含边界）的整点个数。 \(PG\) 右边的同理，和 \(C\) 有关。

感性理解很对，严谨证明不管了（

而操作一下可以发现，新坐标系中斜率为 -1 的直线，在原坐标系中恰好就是 \(-{a+c\over b+d}\) ，与 \({a\over b},{c\over d}\) 都是 Farey neighbour ，所以可以递归求值。更具体地，是递归到

\[S(B_x,B_y,a,b,a+c,b+d)+S(C_x,C_y,a+c,b+d,c,d) \]

4.6 时间复杂度证明

略去（

由于某些原因，需要先暴力计算 \(\min(x,y)<n^{1\over 3}\) 的整点，然后再用上面这个方法，才能保证复杂度。复杂度可以被证明不超过 \(O(n^{1\over 3}\log^3 n)\) ，据说可以被证到 \(O(n^{1\over 3}\log n)\) 。

4.7 优化

把式子变成

\[2\sum_{i=1}^{\sqrt n} \left\lfloor {n\over i}\right\rfloor -\left\lfloor {\sqrt n}\right\rfloor^2 \]

变成统计 \(xy=n\) 下方的 \(y\le \sqrt n\) 的整点数。

可以直接利用 Stern-Brocot Tree 拟合原本的曲线，如下图所示

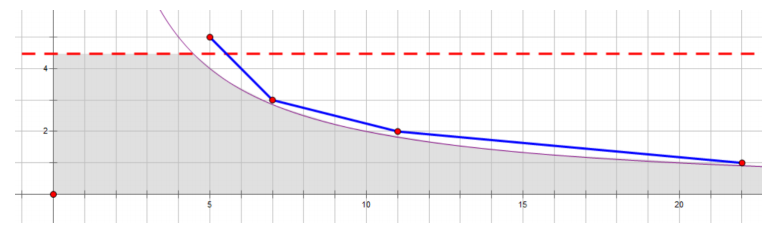
具体怎样拟合呢？假设当前做到了 \((x,y)\) ，那么要在它右边的曲线上方的所有点 \((p,q)\) 中，找到 \({q-y\over p-x}\) 最大且 \(p\) 最小（不清楚为什么要最小）的点，并加上这条折线。显然这么做是满足条件的。

怎样找到这样的 \((p,q)\) 呢？

一开始，我们只有红色虚线上方那一个红色点，以及两个向量 \((1,0),(1,1)\) ，分别对应分数 \({0\over 1},{1\over 1}\) 。把它们加入栈中，栈里面的分数自底向上单调递增。

注意这里的向量的 \(y\) 坐标其实是应该为负数的，但是为了方便就写成非负数。以下加上某个向量的意思都是 \(x\) 坐标相加， \(y\) 坐标相减。

每次我们拿出栈顶向量，并让当前点加上若干个该向量，直到再加一个就会落入曲线下方为止。

现在栈顶的分数已经太大（加上它就会落入曲线下方）了，需要弹栈。一直弹，直到 stk[top] 太大而 st[top-1] 不太大为止。令前者为 \(L\) ，后者为 \(R\) ，则显然有 \(L>R\) 。现在再令 top-- ，即把 \(L\) 弹掉。

现在开始在 SB 树上走，令 \(M={y_L+y_R\over x_L+x_R}\) 。考虑当前点 \(P\) 加上 \(M\) 之后得到的点 \(Q\) 是否在曲线下方。如果不在曲线下方，那么把 \(M\) 压入栈，并令 R=M ，然后继续操作。

否则， 如果 \(|f'(x_Q)|\le R\) ，那么给 \(Q\) 再加上多少个 \(R\) 也不会有用了，所以 \(R\) 就是要找的向量 (?) 。不然就令 L=M 然后继续操作。

这里打了一个 ? ，所以要多说几句。找这个 \((p,q)\) 的过程可以看做在 SB 树上二分，如果每次无脑从 \({0\over 1},{1\over 1}\) 开始二分那么正确性显然是不会有任何问题的（所有可能成为答案的分数都被遍历到了），但那样复杂度就爆炸了。所以这里设置了一个单调栈，把之前二分经过的路径给存下来，找 \((p,q)\) 的过程就变成了先回溯到第一个合法位置，然后再继续往下走。

（也许这是所有要用到 SB 树的题目的通性吧）

由于某些原因，当前点的 \(y<n^{1\over 3}\) 时就要停止迭代，然后暴力计算剩下的答案。这样才能保证复杂度。

用某种方法得到复杂度 \(O \left( n^{1/3} \log n \right)\) ，并且与 4.5 的做法有神奇的内在联系。

4.8 扩展

这里拟合曲线的做法除了复杂度分析和凸性以外没有用到 \(xy=n\) 的任何性质（可能复杂度分析也没有用到？），所以可以很方便地推广到其他奇怪的曲线内部整点计数。