Contrastive and Generative Graph Convolutional Networks for Graph-based Semi-Supervised Learning

动机

• 现有的基于图的方法并没有直接解决 SSL 的核心问题，即监督不足，因此它们的性能仍然非常有限。
• 基于图的半监督学习（SSL ）旨在通过图将少数标记数据的标签转移到剩余的大量未标记数据。作为最流行的基于图的 SSL 方法之一

贡献

• 考虑到特征空间中数据点的相似性提供了原始的监督信号，使用最近兴起的对比学习，结合半监督学习，提出半监督对比学习损失
• 考虑到图拓扑本身包含可以用作 SSL 的补充监督信号，利用生成项来显式建模图和节点表示之间的关系（也就是边预测任务），通过从数据相似性和图结构两个方面探索知识，可以进一步扩展标记数据原本有限的监督信息

思想

框架

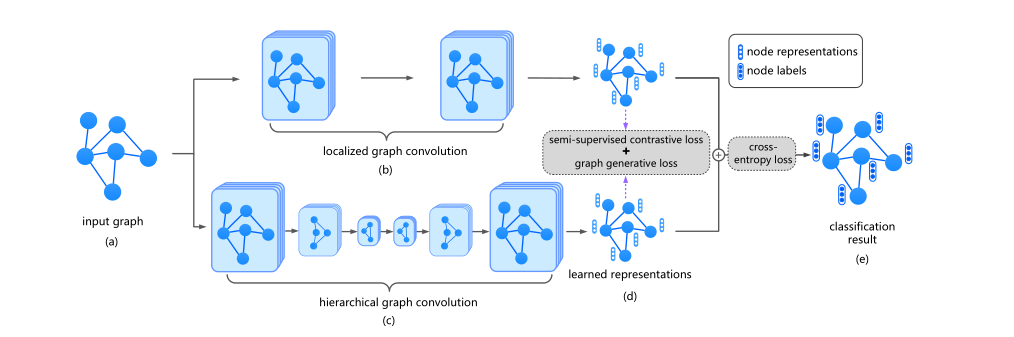
其中(b)和 (c) 表示两种不同的编码器

method

Multi-View Establishment for Graph Convolutions

通过简单的删边加边方式会破坏其语义信息，所以在该方法中都是使用同一个视图，使用不同的编码器GCN HGCN进行编码

采用 GCN 模型作为本地视图 local view 中的主干

HGCN 从全局视图 Golbal view 生成表示

Semi-Supervised Contrastive Learning

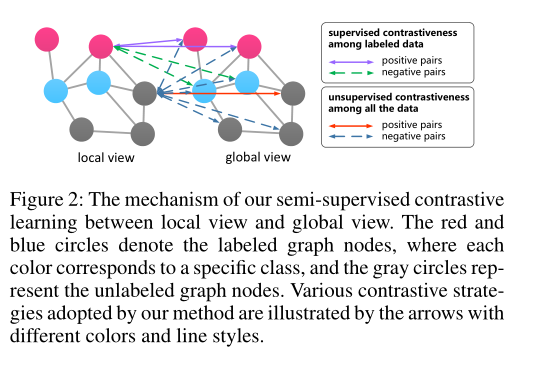
形式上，无监督对比学习有望达到如下效果：

\[\operatorname{score}\left(f\left(\mathbf{x}_{i}\right), f\left(\mathbf{x}_{i}^{+}\right)\right) \gg \operatorname{score}\left(f\left(\mathbf{x}_{i}\right), f\left(\mathbf{x}_{i}^{-}\right)\right) \]

也就是正样本之间的距离远远小于负样本对之间的距离，其中 \(f\) 是编码器，提出的无监督对比损失如下：

\[\mathcal{L}_{u c}=\frac{1}{2 n} \sum_{i=1}^{n}\left(\mathcal{L}_{u c}^{\phi_{1}}\left(\mathbf{x}_{i}\right)+\mathcal{L}_{u c}^{\phi_{2}}\left(\mathbf{x}_{i}\right)\right) \\ \mathcal{L}_{u c}^{\phi_{1}}\left(\mathbf{x}_{i}\right)=-\log \frac{\exp \left(\left\langle\mathbf{h}_{i}^{\phi_{1}}, \mathbf{h}_{i}^{\phi_{2}}\right\rangle\right)}{\sum_{j=1}^{n} \exp \left(\left\langle\mathbf{h}_{i}^{\phi_{1}}, \mathbf{h}_{j}^{\phi_{2}}\right\rangle\right)} \\ \mathcal{L}_{u c}^{\phi_{2}}\left(\mathbf{x}_{i}\right)=-\log \frac{\exp \left(\left\langle\mathbf{h}_{i}^{\phi_{2}}, \mathbf{h}_{i}^{\phi_{1}}\right\rangle\right)}{\sum_{j=1}^{n} \exp \left(\left\langle\mathbf{h}_{i}^{\phi_{2}}, \mathbf{h}_{j}^{\phi_{1}}\right\rangle\right)} \]

其中 \(\phi_{1}、\phi_{2}\) 分别表示 GCN 和 HGCN 编码器，而对于有标签信息的对损失定义如下：

\[\mathcal{L}_{s c}=\frac{1}{2 l} \sum_{i=1}^{l}\left(\mathcal{L}_{s c}^{\phi_{1}}\left(\mathbf{x}_{i}\right)+\mathcal{L}_{s c}^{\phi_{2}}\left(\mathbf{x}_{i}\right)\right) \\ \begin{aligned} \mathcal{L}_{s c}^{\phi_{1}}\left(\mathbf{x}_{i}\right) &=-\log \frac{\sum_{k=1}^{l} \mathbb{1}_{\left[y_{i}=y_{k}\right]} \exp \left(\left\langle\mathbf{h}_{i}^{\phi_{1}}, \mathbf{h}_{k}^{\phi_{2}}\right\rangle\right)}{\sum_{j=1}^{l} \exp \left(\left\langle\mathbf{h}_{i}^{\phi_{1}}, \mathbf{h}_{j}^{\phi_{2}}\right\rangle\right)}, \\ \mathcal{L}_{s c}^{\phi_{2}}\left(\mathbf{x}_{i}\right) &=-\log \frac{\sum_{k=1}^{l} \mathbb{1}_{\left[y_{i}=y_{k}\right]} \exp \left(\left\langle\mathbf{h}_{i}^{\phi_{2}}, \mathbf{h}_{k}^{\phi_{1}}\right\rangle\right)}{\sum_{j=1}^{l} \exp \left(\left\langle\mathbf{h}_{i}^{\phi_{2}}, \mathbf{h}_{j}^{\phi_{1}}\right\rangle\right)}, \end{aligned} \]

其中 \(\mathbb{1}[\cdot]\) 是一个指示函数，如果括号内的参数成立，则等于$ 1\(，否则等于\) 0$。与 无监督对比学习不同。 这里的正负对是根据两个节点是否属于同一类的事实来构造的。换句话说，如果两个示例具有相同的标签，则数据对为正，如果它们的标签不同，则为负

Graph Generative Loss

提取图拓扑信息以更好地指导表示学习过程。在这项工作中，使用图生成损失对图结构进行编码，并对特征表示和图拓扑之间的潜在关系进行建模

\[p\left(\mathcal{G} \mid \mathbf{H}^{\phi_{1}}, \mathbf{H}^{\phi_{2}}\right)=\prod_{i, j} p\left(e_{i j} \mid \mathbf{h}_{i}^{\phi_{1}}, \mathbf{h}_{j}^{\phi_{2}}\right)=\prod_{i, j} \delta\left(\left[\mathbf{h}_{i}^{\phi_{1}}, \mathbf{h}_{j}^{\phi_{2}}\right] \mathbf{w}\right) \\ \mathcal{L}_{g^{2}}=-p\left(\mathcal{G} \mid \mathbf{H}^{\phi_{1}}, \mathbf{H}^{\phi_{2}}\right) \]

实际上使用两个不同模型生成的嵌入进行拼接并且学习一个参数 \(w\) ，就是边预测任务

Model Training

节点预测任务：

\[\mathcal{L}_{c e}=-\sum_{i=1}^{l} \sum_{j=1}^{c} \mathbf{Y}_{i j} \ln \mathbf{O}_{i j} \]

最后总的损失函数：

\[\mathcal{L}=\mathcal{L}_{c e}+\lambda_{s s c} \mathcal{L}_{s s c}+\lambda_{g^{2}} \mathcal{L}_{g^{2}} \]

实验

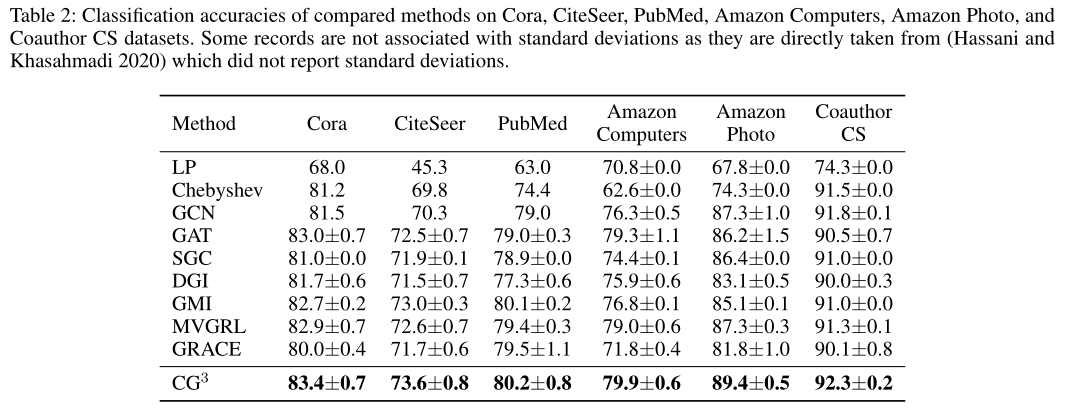
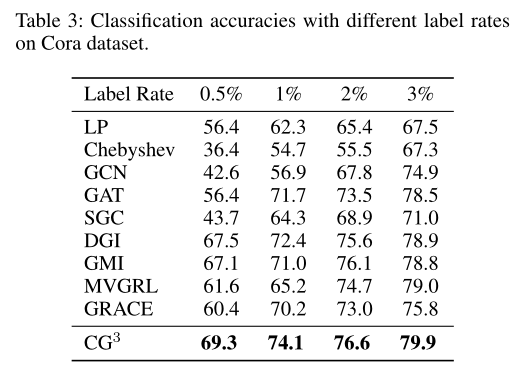
结论

• 半监督任务和对比学习的结合，设计半监督任务的对比损失函数
• 为了不破坏语义信息而使用不同的编码器进行编码得到嵌入，利用嵌入在进行图生成任务
• 使用两个不同的编码器分别获取局部和全局的任务