人工智能实战_第六次作业_王涛

一丶作业要求

标题	内容
这个作业属于哪个课程	班级博客的链接
这个作业的要求在哪里	作业要求的链接
我在这个课程的目标是	完成一个完整的项目，学以致用
这个作业在哪个具体方面帮助我实现目标	帮助我复习DNN

二、解决方法

1) 将模型准确度调整至>97%

其实不修改任何参数只增加epoch就可以很容易超过97%准确率了

1）考虑到梯度下降是在太慢了，对原代码应用了AdamOptimizer。

def adam(w, dw, config=None):
    if config is None: config = {}
    #config.setdefault('learning_rate', 1e-3)
    config.setdefault('beta1', 0.9)
    config.setdefault('beta2', 0.999)
    config.setdefault('epsilon', 1e-8)
    config.setdefault('m', np.zeros_like(w))
    config.setdefault('v', np.zeros_like(w))
    config.setdefault('t', 0)
    
    next_w = None
    config['t']+=1
    config['m'] = config['beta1']*config['m']+(1-config['beta1'])*dw
    config['v'] = config['beta2']*config['v']+(1-config['beta2'])*np.square(dw)
    mt = config['m']/(1-np.power(config['beta1'], config['t']))
    vt = config['v']/(1-np.power(config['beta2'], config['t']))
    next_w = w - config['learning_rate']*mt/np.sqrt(vt+config['epsilon'])

def update3(dict_Param, dict_Grads, learning_rate, config):
    for p, w in dict_Param.items():
        dw = dict_Grads["d"+p]
        config[p]['learning_rate'] = learning_rate
        next_w, next_config = adam(w, dw, config[p])
        dict_Param[p] = next_w
        config[p] = next_config
    return dict_Param, config
#主函数补充
config = {'W1':{}, 'W2':{}, 'W3':{}, 'B1':{}, 'B2':{}, 'B3':{}}
#在Train 补充超参数 config即可

2）在Train中增加了学习率衰减

    for epoch in range(max_epoch):
        learning_rate = learning_rate*0.95

3）用了Relu加快收敛
具体的

def Relu(z):
    mask = z<0
    a = z.copy()
    a[z<0] = 0
    return a

def forward3(X, dict_Param):
    W1 = dict_Param["W1"]
    B1 = dict_Param["B1"]
    W2 = dict_Param["W2"]
    B2 = dict_Param["B2"]
    W3 = dict_Param["W3"]
    B3 = dict_Param["B3"]
    
    Z1 = np.dot(W1,X) + B1
    #A1 = Sigmoid(Z1)
    A1 = Relu(Z1)

    Z2 = np.dot(W2,A1) + B2
    #A2 = Tanh(Z2)
    A2 = Relu(Z2)

    Z3 = np.dot(W3,A2) + B3
    A3 = Softmax(Z3)
    
    dict_Cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2, "Z3": Z3, "A3": A3, "Output": A3}
    return dict_Cache

def backward3(dict_Param,cache,X,Y):
    W1 = dict_Param["W1"]
    W2 = dict_Param["W2"]
    W3 = dict_Param["W3"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    A3 = cache["A3"]
    Z1 = cache['Z1']
    Z2 = cache['Z2']

    m = X.shape[1]

    dZ3= A3 - Y
    dW3 = np.dot(dZ3, A2.T)/m
    dB3 = np.sum(dZ3, axis=1, keepdims=True)/m
    
    dA2 = np.zeros_like(Z2)
    dA2[Z2>0] = 1
    # dZ2 = W3T * dZ3 * dA3
    #dZ2 = np.dot(W3.T, dZ3) * (1-A2*A2) # tanh
    dZ2 = np.dot(W3.T, dZ3)*dA2
    dW2 = np.dot(dZ2, A1.T)/m
    dB2 = np.sum(dZ2, axis=1, keepdims=True)/m
    
    dA1 = np.zeros_like(Z1)
    dA1[Z1>0] = 1
    # dZ1 = W2T * dZ2 * dA2
    #dZ1 = np.dot(W2.T, dZ2) * A1 * (1-A1)   #sigmoid
    dZ1 = np.dot(W2.T, dZ2)*dA1
    dW1 = np.dot(dZ1, X.T)/m
    dB1 = np.sum(dZ1, axis=1, keepdims=True)/m

    dict_Grads = {"dW1": dW1, "dB1": dB1, "dW2": dW2, "dB2": dB2, "dW3": dW3, "dB3": dB3}
    return dict_Grads

引自：Microsoft-ai-edu

2)博客中给出参数列表和对应值

进行了最优参数搜索，列举了9种不同的参数
learning_rate = 0.001887
batch_size = 64
m_epoch = 30

hidden1, hidden2	accuracy
128, 50	0.9787
128, 32	0.9819
128, 16	0.9812
100, 50	0.9821
100, 32	0.983
100, 16	0.9799
64, 50	0.982
64, 32	0.9805
64, 16	0.9815

3)给出最终准确度结果和模型潜能

hard_voting and soft_voting
其实就是保存所有训练时候的输出，hard_voting就是对这些模型进行投票选择，选择多数作为预测输出，soft_voting就是对softmax层输出的概率进行判断，选取模型认为置信概率大的结果作为输出，一般soft_voting是比较好的。
集成方法结果要很好需要模型有足够的差异，犯不同的错误，这样子，集成的结果会比较好。
其实我们可以对模型预测错误的那些实例看看模型对这些实例是如何判断的，可以看到我们可以在模型集成可以提高的程度，毕竟，如果模型对这些错误都完全不知晓，那么这些错误很难在集成时候被发现。
例如对一个test_accuracy: 0.9794的三层DNN，有206个实例预测错误

import matplotlib.pyplot as plt

X = dataReader.XTestSet
y = np.argmax(dataReader.YTestSet, axis=0)
#softmax输出
value = forward3(X, dict_Param)['Output']
#模型预测的最大概率label对应的概率
confidence = value[np.argmax(forward3(X, dict_Param)['Output'], axis=0),np.arange(10000)]
fault_prob = confidence[np.argmax(value, axis=0)!=y]
print(np.sum(confidence[np.argmax(value, axis=0)!=y]>0.97))
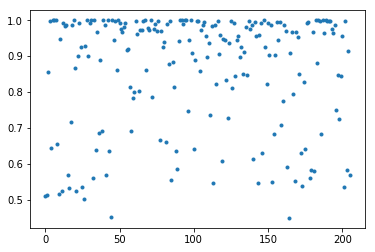
plt.plot(fault_prob, '.')
#output:80

下图我们可以看到，这个模型对一些实例预测其实也不怎么确定，预测概率大于0.97的有80个。进行集成时候，这些错误可能会被其他模型解决。
但是我们dnn结构都一样，这些dnn容易犯同样的‘’错误‘’，所以集成提升空间小了点。

选取所有模型进行hard_voting,选取表现好的4个模型进行soft_voting

from sklearn.metrics import accuracy_score
from scipy.stats import mode
#hard_voting
arr[str(i)+str(j)] = forward3(X, dict_Param)['Output']

ense = np.zeros((10000, 9))
for i, (key,value) in enumerate(arr.items()):
    ense[:,i] = np.argmax(value, axis=0)

accuracy_score(mode(ense[:,:], axis=1)[0], y)
#output 0.9852

#soft_voting
lis = []
confidence_matrix = np.zeros((9, 10000))
for i, (key,value) in enumerate(arr.items()):
    confidence_matrix[i, :]=(value[np.argmax(value, axis=0),np.arange(10000)])

confidence_matrix = confidence_matrix[[1,3,4,6],:]
accuracy_score(ense[:,[1,3,4,6]][np.arange(10000), np.argmax(confidence_matrix, axis=0)], y)
#output 0.9855

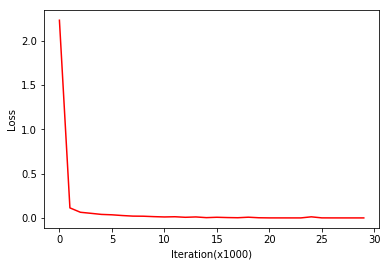
4)损失图