背包问题

01背包问题（选或不选）

有N件物品和一个容量为V的背包。第i件物品体积是 \(c[i]\)，价值是
\(w[i]\)。求解将哪些物品装入背包可使这些物品的占用空间总和不超过背包容量，且价值总和最大。
每一种物品选或不选，一共 \(2^n\) 种情况，可以通过递归实现。

def 背包递归 (物品价值数组，物品体积，背包剩余容量，还有几个物品):
  if 没有空间或没有物品：
    return 0

  放入 = 物品价值 + 背包递归(……, 背包剩余容量 - 当前物品体积，剩余物品 - 1)
  不放入 = 背包递归(……, 背包剩余容量, 剩余物品 - 1)
  返回 取最大值(放入, 不放入)

背包容量为5

	体积	价值
1	1	15
2	3	20
3	4	30
4	2	20

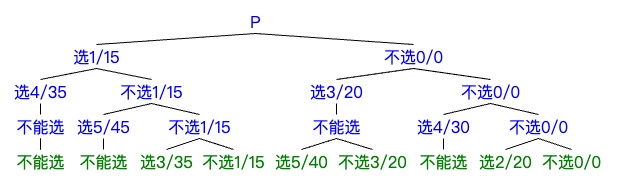
记忆化搜索

使用二维数组dp[剩几个物品][剩余可用空间] =
最大价值，将计算结果结果缓存下来。如果已经计算过了就直接返回答案，经过优化后，时间复杂度和动态规划版本相同。

递归转化为动态规划

把树逆时针转90度从第一个物品到最后一个物品填表格，表格某一列为第i个物品，某一行为容量W。在填表的过程中，例如[i=3:v=4]=30
< [i=2:v=4]=35，我们保留更大的数字。

w\i	1	2	3	4
1	15	15	15	15
2				20
3		20	20	35
4		35	35	35
5			45	45

依次考虑前一个，前两个，前三个，前四个物品。f[i][w]表示前i件物品放入一个容量为w的背包可以获得的最大价值。注意最后答案不一定是f[N][W]而是最后一列的最大的数字，最优解并不一定要把背包装满。

显然，空间复杂度=时间复杂度=行数*列数。

继续优化（优化空间复杂度）

由于必须考虑每个物品放或不放，时间复杂度应该不能再优化了。

思考上面的计算方法，我们发现计算某一列时，只需要上一列的数据。故我们只需要记录一列数据即可。二维数组可以转为一维数组。写出状态转移方程：

\[f[W]=Max(now_v,f[W-w_i]+v_i) \]

注意：若使用两个数组，一个保留上一次数据，一个计算当前数据则无此问题。若只使用一个数组，需要保证更新顺序，f[W]依赖
f[W-w_i]，在更新f[W]时我们必须保证小于W的单元格未被更新，否则状态混乱可能会导致更新一列时，某个物品被多次装入背包，导致更新后的最大价值高于实际值。所以更新时一定要从大到小更新f[W]。

完全背包

一种物品可以选无数个。

如何将该问题转换为01背包问题？
我们可以先装若干个个第一个物品直到装不下，再装若干个第二个物品，以此类推。

	体积	价值
1	1	15
2	3	20
3	4	50

w\i	1	1	1	1	1	2	2	2	3
1	15	15	15	15	15	15	15	15	15
2		30	30	30	30	30	30	30	30
3			45	45	45	45	45	45	45
4				60	60	60	60	60	75
5					75	75	75	75	80

优化

在计算过程中，我们发现在计算同种物品放入若干个的循环中存在许多重复计算。01背包中，从大到小计算可以避免重复装入物品，而本题可以重复装入物品。如果仅将代码改为从小到大遍历是否可以解决此问题呢？建议在纸上动手尝试。

w\i	1	2	3
1	15	15	15
2	30	30	30
3	45	45	45
4	60	60	75
5	75	75	80

经过尝试，发现该方法似乎可以得到正确结果。

严谨证明：写出状态转移方程 \(f[i][W]=max(f[i−1][W],f[i][W−w_i]+v[i])\)
对比01背包问题，注意上一个式子 \(f[W]=Max(now_v,f[W-w_i]+v_i)\) 中 \(f[W-w_i]\)
实际上是 \(f[i-1][W-w_i]\) 而本式中为 \(f[i]\)，故从小往大遍历完全符合该方程。

多重背包问题

增加一个条件，每件物品有\(c_i\)个，也就是不能无限装某个物品。

回顾完全背包如何转为01背包，实际上我们已经解决了该问题。只需要先装\(c_1\)个第一个物品，再装
\(c_2\)
个第二个物品，以此类推。显然优化版本的完全背包算法无法控制最多装几个，不能用来解决此问题。

优化 （这个不用学）

二进制优化

将 n 拆分为 \(2^0+2^1+2^2+...+y\)

比如呢：13 = 1 + 1 + 1 + ... => 1 + 2 + 4 + 6

也就是先装一个再装1个再装2个……

1+2+4->[1,7], 1+2+4+6->[1,7+6]

单调递减队列优化

单调队列的核心问题是为什么需要队列而不仅维护一个最值？单调队列可以解决区间最值或求多个最值，通过提前扔掉不可能在之后的问题中成为最值的元素优化效率。“如果一个人比你小，还比你强，那你就没救了。”
洛谷模板题

下面讲如何优化 洛谷P1776宝物筛选

在计算放入同种物品时，对状态转移进行分组 \(W/w_i\)
使每组之间的状态转移不互相影响。 余数相同的在一组，每组内是一个等差数列
\(+w_i+w_i+...\) 。\(W = k \times w_i + b\)
可以使用一个长度为物品数量的数组进行动态规划计算。若找到
\(dp[b]>dp[a]+(b-a) \times v, a<b\)
则可以扔掉队列中的dp[a]。因为在后续问题中，使用 \(dp[b]\) 计算一定比 \(dp[a]\)
大。既然在计算时只需要最大值，为何不只维护一个最大值，而需要用一个队列呢？若只维护一个最大值，会变为完全背包问题。在计算时，我们需要将已经拿走了规定数量物品的最大项扔掉，用第二个最大项替代它，故需要使用队列。

参考代码：

const { max } = Math;

let n = 3, capacity = 4;
// 价值，体积，数量
let items: [number, number, number][] = [
  [15, 1, 3],
  [20, 3, 2],
  [50, 4, 1],
];
let dp: number[] = [0, 0, 0, 0, 0];

for (let i = 0; i < n; i++) {
  const [value, volume, quantity] = items[i];
  let maxVolume = volume * quantity;
  for (let r = 0; r < volume; r++) {
    const dq: [number, number][] = [];
    for (let k = r + volume; k <= capacity; k += volume) {
      if (dq.length && dq[0][0] > maxVolume) {
        // 拿取数量超过上限
        dq.pop();
      }
      while (
        dq.length &&
        dq.at(-1)![1] + (k - dq.at(-1)![0]) / volume * value <= dp[k]
      ) {
        // 维护单调队列
        dq.pop();
      }
      // 入队
      dq.push([k, dp[k]]);
      // 更新dp数组
      dp[k] = max(dp[k], dq[0][1] + (k - dq[0][0]) / volume * value);
    }
  }
}

console.log(dp);

混合三种背包问题

有的物品只可以取一次（01背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背包）。

这个很简单，循环内判断物品i有多少个，只有一个逆序循环，有无限个顺序循环，有上限的用多重背包算法解决。

如果理解了前面的内容，下面的内容就比较简单了。

二维费用的背包问题

洛谷P1855 榨取kkksc03
多一层循环，其他的和之前完全一致。 $$f[i][a][b] =
max(f[i-1][a][b],f[i-1][a-a_i][b-b_i]+w[i])$$

分组背包

洛谷P1757

#include <iostream>
using namespace std;
int maxWeight, quantity, numberOfGroups;
int groupId;
int group[205][205];
int i, w, k;
int weight[10001], value[10001];
int numberOfItemsInGroup[10001];
int dp[10001];
int main() {
  cin >> maxWeight >> quantity;
  for (i = 1; i <= quantity; i++) {
    // 重量，利用价值，所属组数。
    cin >> weight[i] >> value[i] >> groupId;
    numberOfGroups = max(numberOfGroups, groupId);
    numberOfItemsInGroup[groupId]++;
    group[groupId][numberOfItemsInGroup[groupId]] = i;
  }
  for (i = 1; i <= numberOfGroups; i++) {
    for (w = maxWeight; w >= 0; w--) {
      for (k = 1; k <= numberOfItemsInGroup[i]; k++) {
        if (w >= weight[group[i][k]]) {
          dp[w] = max(dp[w], dp[w - weight[group[i][k]]] + value[group[i][k]]);
        }
      }
    }
  }
  cout << dp[maxWeight];
  return 0;
}

关键在于内层两个循环，计算枚举物品的循环在内层确保组内物品不重复放。