二叉树的遍历

1. 二叉树的定义

二叉树的每个节点包含指向其左、右子节点的指针，我们假设二叉树中保存的值为int型，那么节点的定义如下：

struct BinaryTreeNode {
	int value;
	BinaryTreeNode* lchild;  // left child
	BinaryTreeNode* rchild;  // right child

	BinaryTreeNode(int value, BinaryTreeNode* lchild = nullptr, BinaryTreeNode* rchild = nullptr) {
		this->value = value;
		this->lchild = lchild;
		this->rchild = rchild;
	}
};

现在我们构建一棵如下图所示的二叉树：

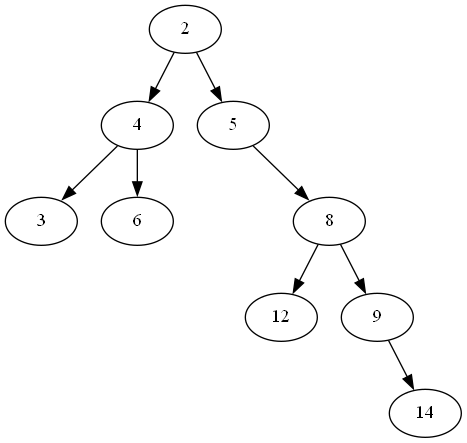
BinaryTreeNode* newBinaryTreeNode(int value, BinaryTreeNode* lchild = nullptr, BinaryTreeNode* rchild = nullptr) {
	// 新建一个二叉树结点
    BinaryTreeNode* node = new BinaryTreeNode(value, lchild=lchild, rchild=rchild);
	return node;
}

BinaryTreeNode* tree = newBinaryTreeNode(2,
	newBinaryTreeNode(4,
		newBinaryTreeNode(3),
		newBinaryTreeNode(6)
	),
	newBinaryTreeNode(5,
		nullptr,
		newBinaryTreeNode(8,
			newBinaryTreeNode(12),
			newBinaryTreeNode(9,
				nullptr,
				newBinaryTreeNode(14)
			)
		)
	)
);

2. 前序、中序和后序遍历

二叉树本身存在着递归结构：它的每一棵子树同样是二叉树。因此，采用递归遍历二叉树会带来很大的方便。

前序、中序和后序遍历的不同主要在于访问每个节点中的值的时机。前序遍历首先访问每个节点的值，再分别遍历左子树、右子树：

void preOrderVisit(BinaryTreeNode* tree) {
	if (tree != nullptr) {
		std::cout << tree->value << " ";  // 首先访问当前节点的值
		preOrderVisit(tree->lchild);  // 随后遍历其左子树
		preOrderVisit(tree->rchild);  // 最后遍历其右子树
	}
}

中序遍历则是先遍历左子树，然后访问节点的值，最后遍历其右子树：

void midOrderVisit(BinaryTreeNode* tree) {
	if (tree != nullptr) {
		midOrderVisit(tree->lchild);  // 首先遍历左子树
		std::cout << tree->value << " ";  // 访问当前节点的值
		midOrderVisit(tree->rchild);  // 最后遍历右子树
	}
}

 而后序遍历首先遍历其左、右子树，最后访问当前节点的值：

void postOrderVisit(BinaryTreeNode* tree) {
	if (tree != nullptr) {
		postOrderVisit(tree->lchild);  // 首先遍历左子树
		postOrderVisit(tree->rchild);  // 随后遍历右子树
 		std::cout << tree->value << " ";  // 最后访问当前节点的值
	}
}

对于上面图示的二叉树，它的前序、中序、后序遍历结果为：

(前序): 2 4 3 6 5 8 12 9 14

(中序): 3 4 6 2 5 12 8 9 14

(后序): 3 6 4 12 14 9 8 5 2

3. 按层遍历

对于上图所示的二叉树，可以看出不同的节点具有不同的深度，有时候我们需要按照节点所处的深度，一层一层地遍历二叉树。例如，对于上面图示的二叉树，我们希望按层遍历的结果为：

2
4 5
3 6 8
12 9
14

按层遍历也不是太难，不过我们需要借助一个队列。每次从队列取出头节点，将它的左、右子节点加入队列，重复这一步骤，直到队列为空。

void levelOrderVisit(TreeNode* root) {
    if (root != nullptr) {
        queue<TreeNode*> q;
        q.push(root);  // 将根节点压入队列(第1层)

        while (!q.empty()) {
            int size = q.size();  // size是当前层的节点个数
            vector<int> levelOutput(size);
            for (int i = 0; i < size; ++i) {  
                // 遍历当前层的每一个节点
                auto element = q.front();
                q.pop();

                // 访问当前层的节点
                std::cout << element->val << " ";

                // 压入下一层的节点
                if (element->left != nullptr) {
                    q.push(element->left);
                }
                if (element->right != nullptr) {
                    q.push(element->right);
                }
            }
            std::cout << std::endl;
        }
    }
}