【CV】吴恩达机器学习课程笔记第16章 | CSDN创作打卡
本系列文章如果没有特殊说明,正文内容均解释的是文字上方的图片
机器学习 | Coursera
吴恩达机器学习系列课程_bilibili
16 推荐系统
16-1 问题规划
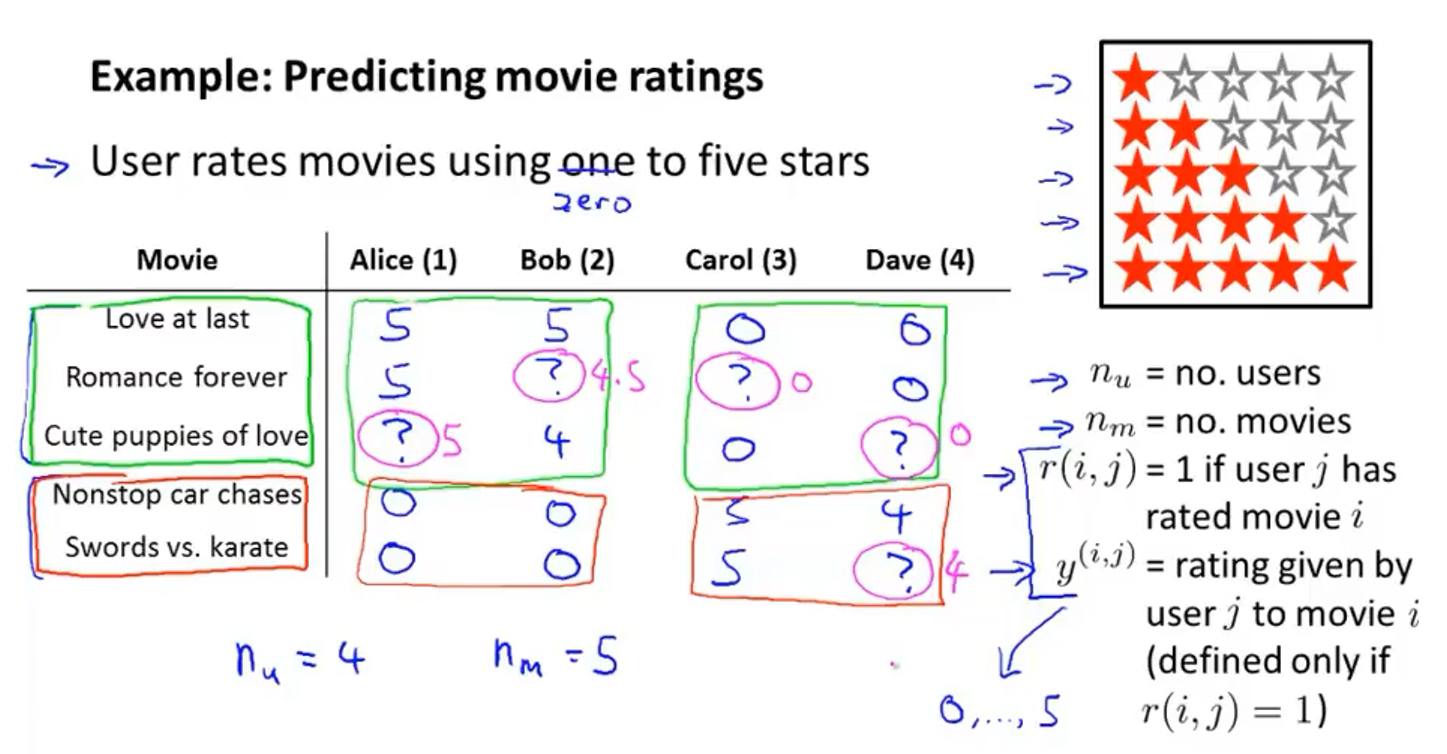
以电影评分预测系统为例,机器学习系统需要预测问号处的值来决定向用户推荐哪部电影
- n u n_u nu表示用户的数量,这里=4
- n m n_m nm表示电影的数量,这里=5
- r ( i , j ) r(i,j) r(i,j):如果用户 j j j已经给电影 i i i进行评分了的话, r ( i , j ) = 1 r(i,j)=1 r(i,j)=1
- y ( i , j ) y^{(i, j)} y(i,j)表示用户 j j j给电影 i i i的评分(仅在 r ( i , j ) = 1 r(i,j)=1 r(i,j)=1时才有定义)
16-2 基于内容的推荐算法
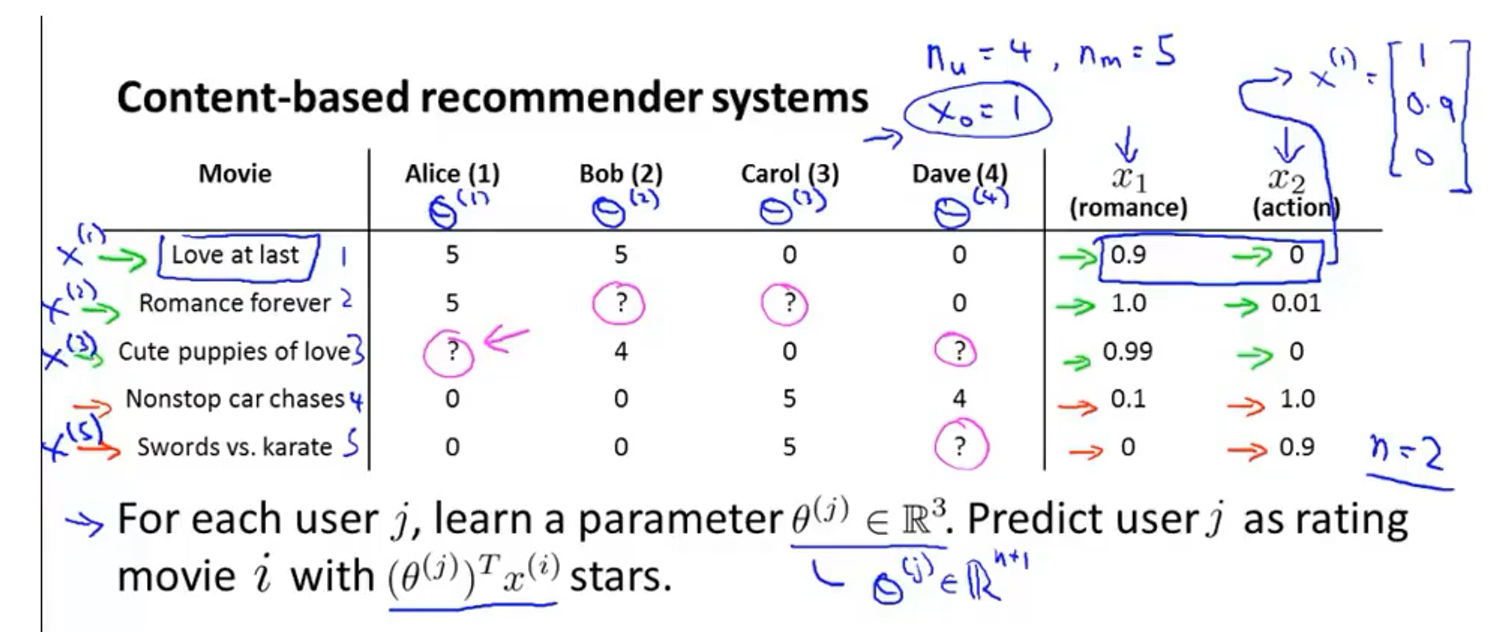
- 用两个特征 x 1 x_1 x1和 x 2 x_2 x2分别表示一部电影的浪漫片程度和动作片程度,组合成矩阵并加上 x 0 = 1 x_0=1 x0=1,比如 x ( 1 ) = [ 1 0.9 0 ] x^{(1)}=\left[\begin{array}{l} 1 \\ 0.9 \\ 0 \end{array}\right] x(1)=⎣⎡10.90⎦⎤, x ( i ) x^{(i)} x(i)表示的是第 i i i部电影的特征向量
- 对每一个用户 j j j都学习出一个参数 θ ( j ) ∈ R 3 \theta^{(j)} \in \mathbb{R}^{3} θ(j)∈R3,预测出用户 j j j对电影 i i i的评价星级为 ( θ ( j ) ) T x ( i ) \left(\theta^{(j)}\right)^{T} x^{(i)} (θ(j))Tx(i)
得到推荐算法的代价函数为:
1
2
m
(
j
)
∑
i
:
r
(
i
,
j
)
=
1
(
(
θ
(
j
)
)
⊤
(
x
(
i
)
)
−
y
(
i
,
j
)
)
2
+
λ
2
m
(
j
)
⋅
∑
k
=
1
n
(
θ
k
(
j
)
)
2
\frac{1}{2 m^{(j)}} \sum_{i: r(i, j)=1}\left(\left(\theta^{(j)}\right)^{\top}\left(x^{(i)}\right)-y^{(i, j)}\right)^{2}+\frac{\lambda}{2 m^{(j)}} \cdot \sum_{k=1}^{n}\left(\theta_{k}^{(j)}\right)^{2}
2m(j)1i:r(i,j)=1∑((θ(j))⊤(x(i))−y(i,j))2+2m(j)λ⋅k=1∑n(θk(j))2
其中
m
(
j
)
m^{(j)}
m(j)表示用户
j
j
j评价了的电影数量
∑
i
:
r
(
i
,
j
)
=
1
\sum_{i: r(i, j)=1}
∑i:r(i,j)=1表示累加所有满足
r
(
i
,
j
)
=
1
r(i, j)=1
r(i,j)=1的项,变化
i
i
i
为了简化计算,一般去掉
m
(
j
)
m^{(j)}
m(j)项,代价函数变为:
1
2
∑
i
:
r
(
i
,
j
)
=
1
(
(
θ
(
j
)
)
⊤
(
x
(
i
)
)
−
y
(
i
,
j
)
)
2
+
λ
2
⋅
∑
k
=
1
n
(
θ
k
(
j
)
)
2
\frac{1}{2 } \sum_{i: r(i, j)=1}\left(\left(\theta^{(j)}\right)^{\top}\left(x^{(i)}\right)-y^{(i, j)}\right)^{2}+\frac{\lambda}{2 } \cdot \sum_{k=1}^{n}\left(\theta_{k}^{(j)}\right)^{2}
21i:r(i,j)=1∑((θ(j))⊤(x(i))−y(i,j))2+2λ⋅k=1∑n(θk(j))2

要优化所有用户的参数,代价函数改为:
J
(
θ
(
1
)
,
…
,
θ
(
n
u
)
)
=
1
2
∑
j
=
1
n
u
∑
i
:
r
(
i
,
j
)
=
1
(
(
θ
(
j
)
)
T
x
(
i
)
−
y
(
i
,
j
)
)
2
+
λ
2
∑
j
=
1
n
u
∑
k
=
1
n
(
θ
k
(
j
)
)
2
J\left(\theta^{(1)}, \ldots, \theta^{\left(n_{u}\right)}\right)=\frac{1}{2} \sum_{j=1}^{n_{u}} \sum_{i: r(i, j)=1}\left(\left(\theta^{(j)}\right)^{T} x^{(i)}-y^{(i, j)}\right)^{2}+\frac{\lambda}{2} \sum_{j=1}^{n_{u}} \sum_{k=1}^{n}\left(\theta_{k}^{(j)}\right)^{2}
J(θ(1),…,θ(nu))=21j=1∑nui:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2

梯度下降更新项如上↑
16-3 协同过滤
由于之前的推荐算法的数据集中是给定了每部电影的特征,而一般一部电影的特征是难以判断的,所以需要协同过滤
来自动学习特征
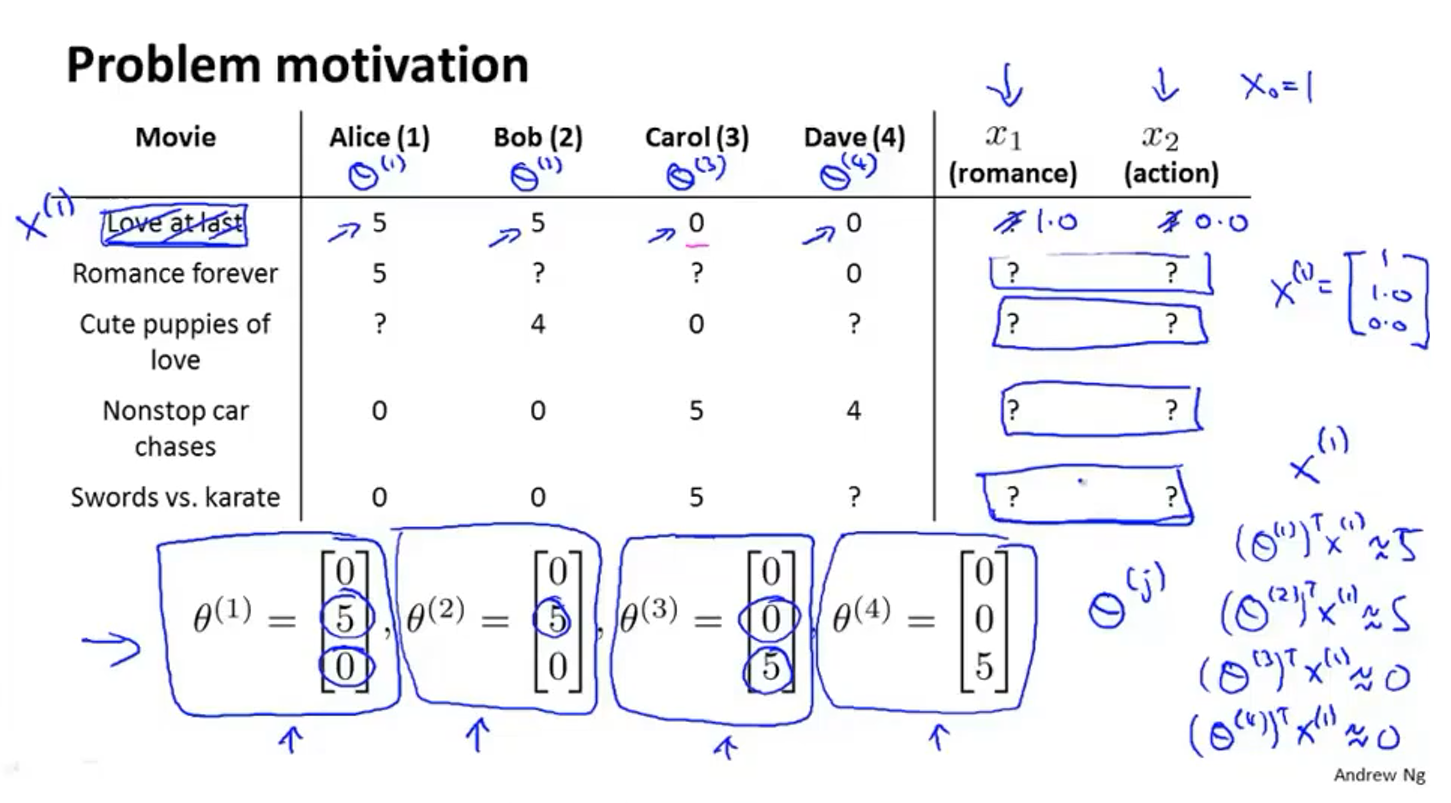
调查每位用户对电影类型的喜好得到参数矩阵
θ
\theta
θ,比如
θ
(
1
)
=
[
0
5
0
]
\theta^{(1)}=\left[\begin{array}{l} 0 \\ 5 \\ 0 \end{array}\right]
θ(1)=⎣⎡050⎦⎤表示的是用户1对
x
1
x_1
x1表示的浪漫片有5的喜爱,对
x
2
x_2
x2表示的动作片有0的喜爱,矩阵第一项的存在是因为有
x
0
=
1
x_0=1
x0=1这一项
根据用户给出的对一类电影的喜爱程度、用户给出的对电影的评分,就可以计算每一部电影的特征值
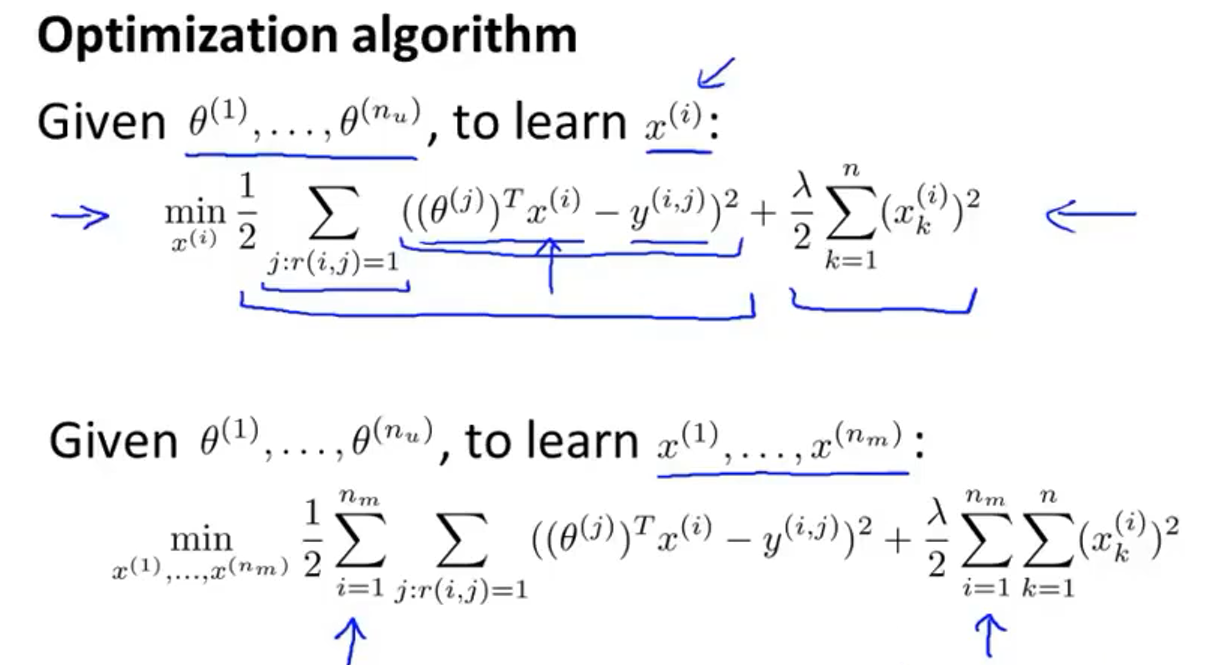
通过上图的代价函数计算出每一部电影的合适的特征

先猜测一组参数
θ
\theta
θ,然后计算出电影的特征
x
x
x,再根据此特征计算新的参数
θ
\theta
θ,再计算出电影的特征
x
x
x,这样不断循环,最后就能收敛
16-4 协同过滤算法
去掉
x
0
=
1
x_0=1
x0=1和
θ
0
=
1
\theta_0=1
θ0=1,让
x
∈
R
n
x \in \mathbb{R}^{n}
x∈Rn,
θ
∈
R
n
\theta \in \mathbb{R}^{n}
θ∈Rn

把求
θ
\theta
θ和求
x
x
x的两个代价函数合起来,得到一个新的不需要像上一节一样循环往复的代价函数:
J
(
x
(
1
)
,
…
,
x
(
n
m
)
,
θ
(
1
)
,
…
,
θ
(
n
u
)
)
=
1
2
∑
(
i
,
j
)
:
r
(
i
,
j
)
=
1
(
(
θ
(
j
)
)
T
x
(
i
)
−
y
(
i
,
j
)
)
2
+
λ
2
∑
i
=
1
n
m
∑
k
=
1
n
(
x
k
(
i
)
)
2
+
λ
2
∑
j
=
1
n
u
∑
k
=
1
n
(
θ
k
(
j
)
)
2
J\left(x^{(1)}, \ldots, x^{\left(n_{m}\right)}, \theta^{(1)}, \ldots, \theta^{\left(n_{u}\right)}\right)=\frac{1}{2} \sum_{(i, j): r(i, j)=1}\left(\left(\theta^{(j)}\right)^{T} x^{(i)}-y^{(i, j)}\right)^{2}+\frac{\lambda}{2} \sum_{i=1}^{n_{m}} \sum_{k=1}^{n}\left(x_{k}^{(i)}\right)^{2}+\frac{\lambda}{2} \sum_{j=1}^{n_{u}} \sum_{k=1}^{n}\left(\theta_{k}^{(j)}\right)^{2}
J(x(1),…,x(nm),θ(1),…,θ(nu))=21(i,j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2+2λj=1∑nuk=1∑n(θk(j))2

上图是协同过滤算法的全过程:
- 初始化 x x x和 θ \theta θ为一个很小的值
- 用梯度下降或其他优化算法最小化代价函数
- 得出最后的 x x x和 θ \theta θ即可计算某个用户未评价的电影的可能的评价星级
16-5 向量化:低秩矩阵的分解
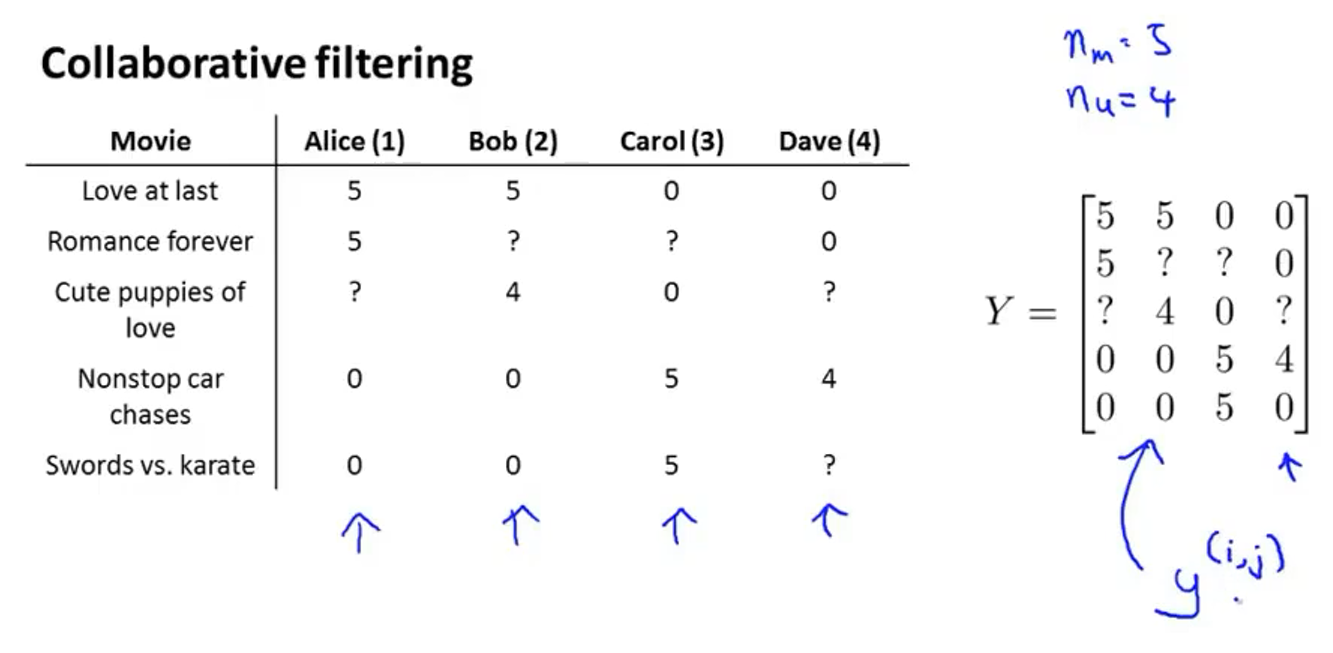
首先把上图的数据表写成矩阵
Y
Y
Y
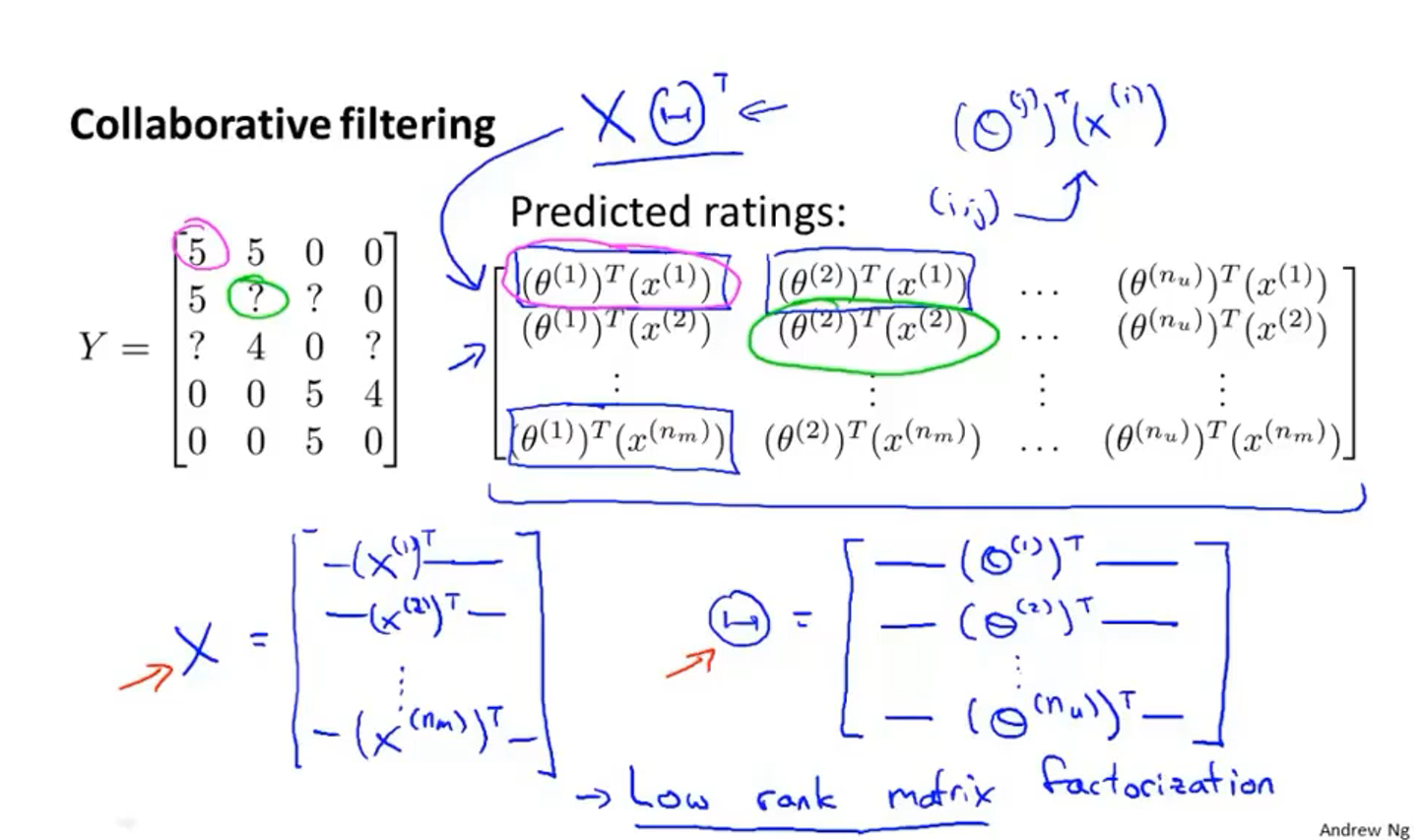
矩阵
Y
Y
Y中的每一个元素都是由公式
(
θ
(
j
)
)
⊤
(
x
(
i
)
)
\left(\theta^{(j)}\right)^{\top}\left(x^{(i)}\right)
(θ(j))⊤(x(i))计算得出的
矩阵
X
X
X和矩阵
Θ
\Theta
Θ由上图所示的元素组成,所以矩阵
Y
Y
Y可以表示为
Y
=
X
Θ
T
Y=X \Theta^{T}
Y=XΘT

如何找到跟一部电影相似的另一部电影?
- ∥ x ( i ) − x ( j ) ∥ \left\|x^{(i)}-x^{(j)}\right\| ∥∥x(i)−x(j)∥∥越小,表示电影 i i i和电影 j j j越相似
16-6 实施细节:均值归一化
如果一位用户没有对任何一部电影评分,那么会得出预测他对所有电影的评分都为0的荒谬结果,所以需要均值归一化
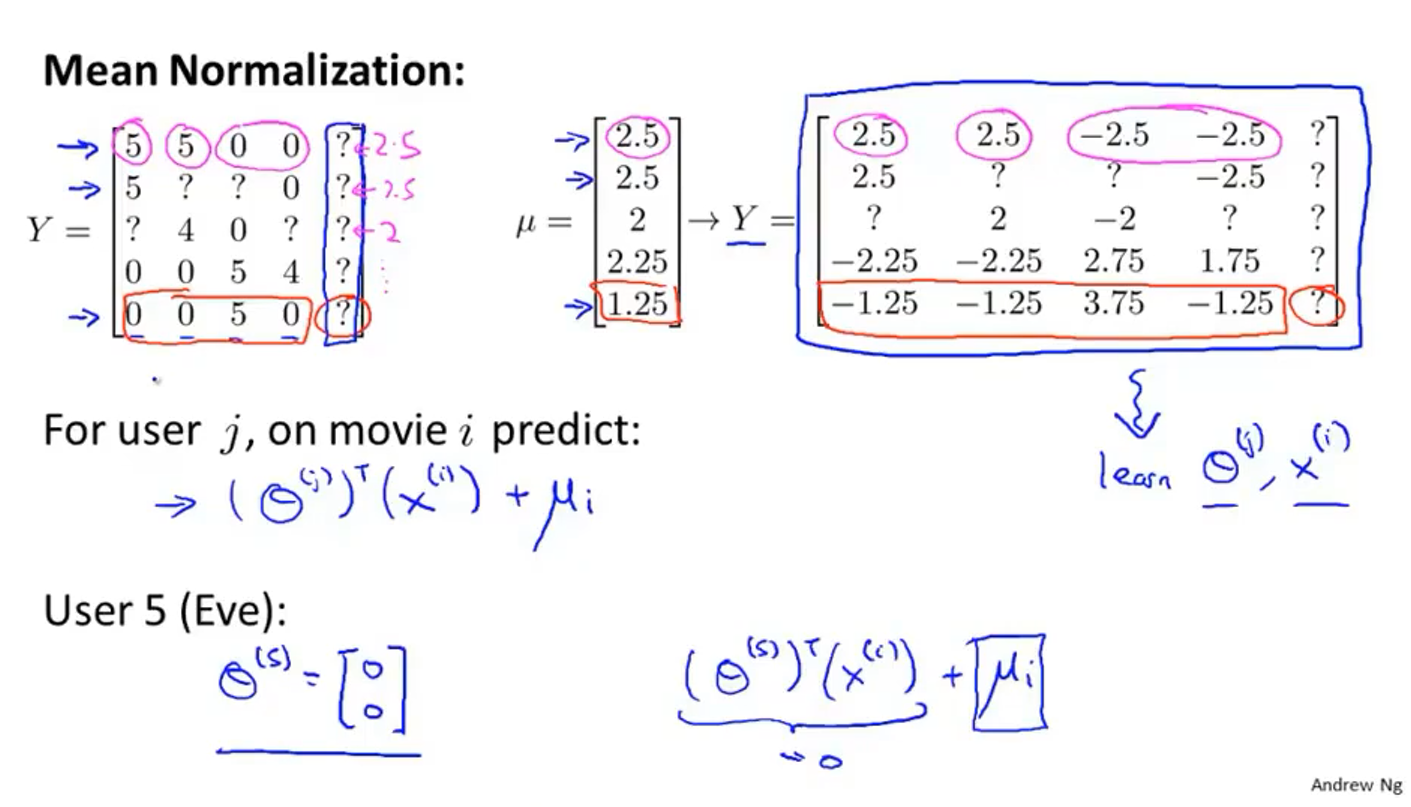
如上图所示,跟上一节相同的矩阵
Y
Y
Y,求每一部电影的评分均值得到矩阵
μ
\mu
μ,然后把矩阵
Y
Y
Y中的每一项都减去矩阵
μ
\mu
μ中对应的电影的平均值,得到新的矩阵
Y
Y
Y,按照新的矩阵来学习出
θ
(
i
)
\theta^{(i)}
θ(i)和
x
(
i
)
x^{(i)}
x(i),最后在计算某一个未知的评分时需要用公式
(
θ
(
j
)
)
⊤
(
x
(
i
)
)
+
μ
i
\left(\theta^{(j)}\right)^{\top}\left(x^{(i)}\right)+\mu_{i}
(θ(j))⊤(x(i))+μi,(因为之前平均值被减掉了,所以现在要加回去),这样预测用户5时得到的结果就不再时0,而是预测的电影的评分平均值
本文来自博客园,作者:Fannnf,转载请注明原文链接:https://www.cnblogs.com/overtop/p/15890738.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号