深度学习——正则化
深度学习——正则化
作者：Oto_G
全是自我理解，表达不严谨，仅供参考
本文默认正则化范数为L1范数
这是今天讨论的问题：
- 为什么融入正则的损失函数能够防止过拟合
- 为什么正则融入损失函数的形态是：原损失函数 + 范数
- 范数是啥
防止过拟合
过拟合，通俗来说就是，你的参数训练的太好了，以至于这组参数只能在你的训练数据上有好的表现 XD
遇到过拟合先冷静下来，因为你遇到的情况可能比你想得还要糟糕，下面是产生过拟合的两种情况，仅供参考 XD
- 给的训练参数太多了，导致过拟合。如果是这种情况，恭喜你，今天所讲的就是针对它的解决方法 ヽ(°▽°)ノ
- 训练数据和测试数据不兼容，通俗来讲，你的训练数据或者是测试数据有问题，但你误以为是模型过拟合了。如果是这种情况，晚安，玛卡巴卡
好的，说完过拟合，我们回到第一个问题，为什么融入正则的损失函数能够防止过拟合
可以看到标题已经给出了模型过拟合后的一种解决方案，就是将你的损失函数稍加修改，把正则化这个概念引入你的损失函数
不用担心，引入正则化非常简单，但还是先来看下啥是正则化
首先，和正则表达式区分一下，在了解正则化前呢，请告诉自己，正则表达式和正则化没有任何关系:P
正则化以我的理解就是，将你训练的参数向量（矩阵）在最小化模型影响地情况下，尽可能地稀疏化
稀疏矩阵是数值计算中普遍存在的一类矩阵，主要特点是绝大部分的矩阵元素为零
假设你没有使用正则化训练好的参数是左图，那么正则化就是让这个参数尽可能地变成右图，甚至为一些参数直接为0
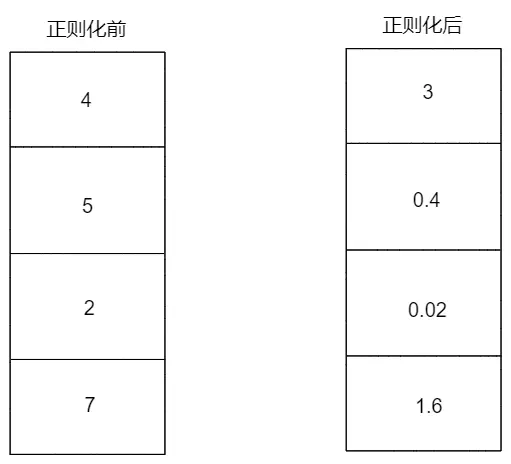
这样之后，我们再想想，之前过拟合是由于参数太多导致的，正则化之后，部分参数的权重接近于零，那么就相当于该参数对模型的影响大幅减小，那么也就不会过拟合了
- 可能这时候有同学会想到，如果引入正则化导致部分参数降低了对模型的影响，会不会降低错参数导致模型效果不佳呀？
- 答：正则化完全不会降低错参数。首先模型的收敛还是靠损失函数决定，而正则化只是对损失函数进行线性相加，不会导致损失函数意义改变，所以训练后的参数还是适配模型的。反过来讲，正则化之所以能够做到将参数稀疏化，又能保持适配模型，就是靠的其参与到损失函数优化过程中（直接将范数加在了损失函数后面）
正则融入损失函数的形态
接着上面一段，最后说到，正则化之所以能够做到将参数稀疏化，又能保持适配模型，就是靠的其参与到损失函数优化过程中（直接将范数加在了损失函数后面）
这里引出范数的概念，专业解释可以查下权威书籍，通俗来说，举个例子：有一个参数向量，那么L2范数就是这个参数向量到坐标原点的欧氏距离
具体Lp的范式定义如下，xi为参数向量或矩阵
- L1范数：参数的绝对值之和
- L2范数：参数与原点的欧氏距离
而正则化就是在原来的损失函数基础上加上L1范数（有时也会L2）乘以权重
权重（这是个超参数，需要先行给定）就是用来调整模型在泛化能力和拟合能力上的关系的，一般设0.1，根据训练情况可以自行调整
直观体会
进入http://playground.tensorflow.org/
配置成如图所示的状态，红色实线框为需要调整的地方，虚线框即为正则化选项（范数和权重），点击左上角按钮即可训练。可以自行尝试选择不同的范数和权重，看看训练结果会如何
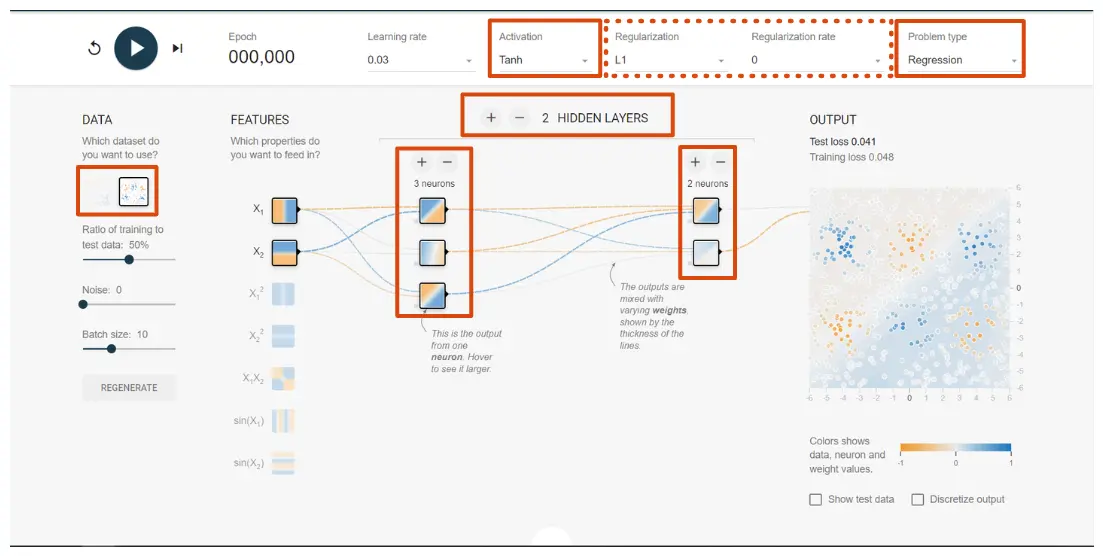
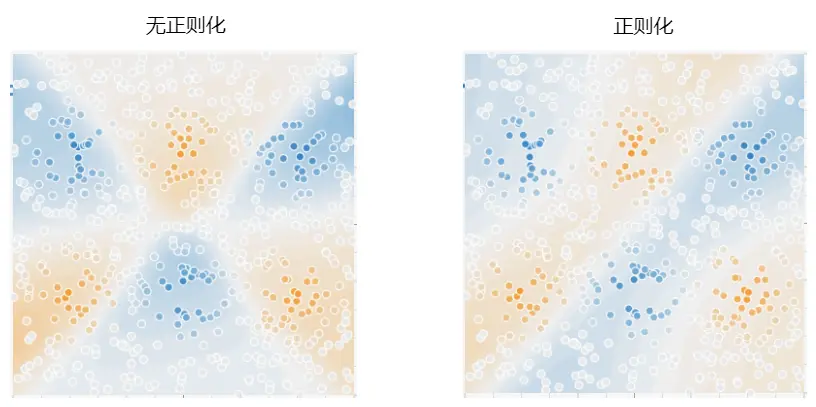
下面给出我的训练结果
