LC5-Longest Palindromic Substring

https://leetcode.com/problems/longest-palindromic-substring/

经典问题，求字符串中的最长回文子串

 

O(N³)解法：

枚举字符串的所有子串，然后判断子串是否回文

 

O(N²)解法：

先用特殊字符填充字符串，以处理偶数长度的回文串

枚举每个位置的字符为中心，向两侧延展求最长回文子串

 

Manacher算法：

Manacher是优化的中心匹配算法，利用之前已经算出的信息来加速后续的匹配。

依然先对字符串进行加倍来处理偶数长度的回文串。

设p[i]为以第i个字符为中心，最长回文子串的半径长度。p[i]=1，则回文串为它自身，p[i]=2，则回文串总长度为3。设mx为上一次操作中处理到的最右端的下标。设center为上一次操作中的回文串中心位置。

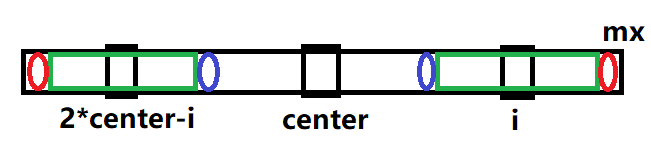
在求p[i]时，找到i相对于center的对称点2*center-i，如果对称点的回文半径包含在总体范围内，则根据回文串特性，p[i]=p[2*center-i]，且向外拓展必然失去匹配。

如果对称点的回文半径很长，超出了总体范围，由于mx之外的部分我们无从得知，因此需要进行暴力匹配。先令p[i]=mx-i，然后开始向外暴力匹配，看是否依然为回文。

当这一次操作的回文半径超出mx时，我们更新mx的值并将center更新为i。

Manacher算法的核心思路其实就是在计算p[i]时，不从半径为1开始重新计算，而是根据前面的计算结果，从一个更大的初始半径开始匹配，算法的复杂度为O(N)。

class Solution {
public:
    string longestPalindrome(string s) {
        string s_modify;
        s_modify.push_back('$');
        s_modify.push_back('#');
        int len = s.size();
        for (int i = 0; i < len; i++) {
            s_modify.push_back(s[i]);
            s_modify.push_back('#');
        }
        s_modify.push_back('*');

        len = s_modify.length();
        vector<int> p(len,0);
        p[0] = 1;
        int mx = 0, center = 0;
        for (int i = 1; i < len; i++) {
            if (mx > i) p[i] = min(p[2 * center - i], mx - i);
            else p[i] = 1;
            while (s_modify[i + p[i]] == s_modify[i - p[i]])
                p[i]++;
            if (i + p[i] > mx) {
                mx = i + p[i];
                center = i;
            }
        }

        int pos = 0, MaxExpand = 0;
        int SIZE = p.size();
        for (int i = 0; i < SIZE; i++) {
            if (p[i] > MaxExpand) {
                pos = i;
                MaxExpand = p[i];
            }
        }

        string ret = "";
        for (int i = pos - MaxExpand + 1; i <= pos + MaxExpand - 1; i++) {
            if (s_modify[i] != '#' && s_modify[i] != '$' && s_modify[i] != '*') {
                ret.push_back(s_modify[i]);
            }
        }

        return ret;
    }
};