11 月记录

[NOIP2024] 树上查询 主流与非主流做法

直接在树上预处理出 \(\mathcal O(n)\) 个段 \((l,r,t)\) 表示区间 \([l,r]\) 的所有子区间的 LCA 在 \(t\) 子树内。

方法是每个子树维护出现的编号连续段，启发式合并两个联通块，将其连续段合并。

则现在问题变成与询问区间交 \(\ge k\) 的段都可以有贡献。

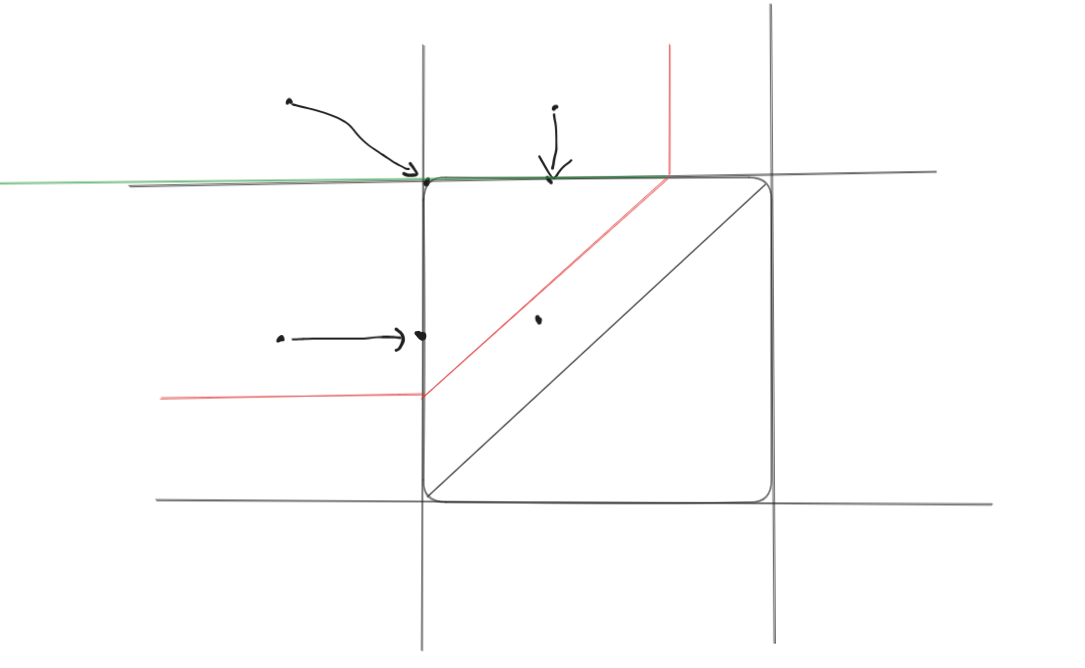
即查红色区域贡献最大值。

分成上下两个部分，分别是两个二维数点，就做完了。

---

另外一种方法。

考虑扫描线，向右扫到 \(i\) 时对其所有祖先 \(j\) 维护 \(len_j\) 表示 \([i-len_j+1,i]\) 这个后缀点在 \(j\) 子树内。

修改就是设 \(anc=lca(i-1,i)\)，将 \([dep_{anc}+1,dep_{i-1}]\) 清空，将 \([1,dep_i]\) 加一。

问题变成查询链上 \(\ge k\) 的最大位置。

发现所有操作修改的连续段是 \(\mathcal O(n)\) 的，每个连续段最后一个点存在贡献，且连续段在删除之前值不断变大，故连续段只有在最后贡献时刻的贡献有用。

对于 \([l,r]\) 还没有删除的连续段贡献，在 \(r\) 处线段树二分即可。

对于之前删除的连续段，对连续段考虑，设扫到 \(i\) 删除，最深点为 \(j\)，则能贡献到的询问为 \(l+k-1\le i\le r\) 且 \(k\le len_j\)。

这也是二维的形式，不过这是贡献，不是查询，所以可能是比较新奇的维护方法！

扫 \(k\)，每次加入一个连续段操作为区间取 \(\max\)，加入询问需要将之前的贡献删除。

P11516 [CCO 2024] Summer Driving

https://csdiy.wiki/必学工具/Vim/#vim_1

https://wsdjeg.net/wiki/learn-vim/ch04_vim_grammar/

CF1608F MEX counting

给定整数 \(n, k\)，以及一个数组 \([b_1, b_2, \ldots, b_n]\)。

请你求满足以下条件的数组 \([a_1, a_2, \ldots, a_n]\) 的个数：

• 对于每个 \(i\)，\(0 \le a_i \le n\)。
• 对于每个 \(i\)，都有 \(|\operatorname{mex}([a_1, a_2, \ldots, a_i]) - b_i| \le k\)。

\(n\le 2000,0\le k\le 50\)。

---

我们需要知道 dp 过程中 \(\operatorname{mex}\) 的值，但是肯定又不能记录下所有的数。

不妨只确定所有 \(<\operatorname{mex}\) 的数，而 \(>\operatorname{mex}\) 的数记录下有多少种，后面再分配。

• 加入一个非 \(\operatorname{mex}\) 的数，则 \(\operatorname{mex}\) 不变。
  • 若 \(<\operatorname{mex}\)，直接确定他的取值。
  • 若 \(>\operatorname{mex}\)：
    • 一种新的数。
    • 已经出现过的数：分配他属于哪一种。
• 加入了 \(\operatorname{mex}\)，枚举新的 \(\operatorname{mex}=k\)，则 \((\operatorname{mex},k)\) 这些值需要存在，对之前 \(>\operatorname{mex}\) 的等价类分配 \((mex,k)\) 这些值即可。

???

给一个长度为 \(n\) 的方块序列，每个方块有一个颜色，每次消除一段颜色相同长度为 \(x\) 的方块，并获得 \(x^2\) 的分数，消除后剩下的方块会合并起来。

求最大的得分。

\(n\le 200\)。

---

P14364 [CSP-S 2025] 员工招聘

给出长度为 \(n\) 的 \(01\) 串 \(s\)，有 \(n\) 个人来面试，每个人有权值 \(c_i\in[0,n]\)。

对于 \(n!\) 种面试顺序，若 \(i\) 在第 \(j\) 天来面试，若 \(s_j=0\)，他直接离开；否则若前面天离开的人数 \(\ge c_i\)，他也离开。

求有多少种面试顺序使得至少 \(m\) 个人不离开。

\(m\le n\le 500\)。

---

钦定每个位置的人是否离开，带来的限制 \(c \le pre\) 或 \(c>pre\)，需要计算对应的排列数量。

考虑对 \(c \le pre\) 的位置（不合法）直接放人，\(c>pre\) 的位置（合法）先记录下来，当 \(pre\leftarrow pre+1\) 时再对这些位置分配。

设 \(f_{i,j,k}\) 表示考虑 \([1,i]\)，当前有 \(j\) 个 \(>k\) 的位置还未确定，当前 \(pre=k\)，的方案数。

我们知道前面填了 \(i-j\) 个 \(\le k\) 的人。

• \(s_i=1\)

  • 钦定这个位置 \(\le k\)，直接在剩下 \(sum_{k}-(i-j)\) 个 \(\le k\) 的人中选择一个。
  • \(>k\)：先将当前位置加入 \(>k\) 的未分配的集合中，再对前面分配 \(k+1\)。
    • 分配：枚举 \(p\in[0,\min(tot_{k+1},j)]\) 个未确定位置，对其分配 \(k+1\)，后面也是类似的。

• \(s_i=0\)

  • 钦定这个位置 \(\le k\)，则当前位置需要先在剩下 \(sum_{k}-(i-j)\) 个 \(\le k\) 的人中选择一个，对前面的分配 \(k+1\)。
  • \(>k\)：先加入 \(>k\) 的未分配的集合中，对前面分配 \(k+1\)。

时间复杂度 \(\mathcal O(n^3)\)，这是因为分配时枚举的上界为 \(tot_{k+1}\)，总和为 \(\mathcal O(n)\)。

P10538 [APIO2024] 星际列车

有 \(n\) 个行星，有 \(m\) 辆星际列车，第 \(i\) 辆列车在时刻 \(a_i\) 从行星 \(x_i\) 出发，在时刻 \(b_i\) 到达行星 \(y_i\)，代价为 \(c_i\)。换乘条件为上一辆车的终点和下一辆车的起点相同，且上一辆车到达时刻 \(\le\) 下一辆车出发时刻。

同时你需要吃 \(w\) 顿饭，第 \(i\) 顿饭必须在 \([l_i,r_i]\) 时刻吃。如果在列车上吃则免费，如果在 \(i\) 号行星吃则代价为 \(t_i\)。

时刻 \(0\)，你在 \(1\) 号行星上，求到达 \(n\) 号行星的最小代价。

\(n,m,w\le 10^5,1\le a_i<b_i\le 10^9,1\le c_i\le 10^9,1\le l_i\le r_i\le 10^9,1\le t_i\le 10^9\)。

---

暴力的想法是将位置、时间作为状态，但是其实只有 \((a_i,x_i),(b_i,y_i)\) 这些是有用的。

设 \(f_i\) 表示坐完第 \(i\) 辆列车的最小代价：

\[f_i\leftarrow \min_{b_j\le a_i,y_j=x_i}f_j+g(b_j,a_i)\times t_{x_i}+c_i \]

其中 \(g(x,y)\) 表示完全包含于 \((x,y)\) 的 \([l_i,r_i]\) 个数，使用在线二维数点可以快速得到一个值。

将已转移列车按照 \(y_j\) 分类，按照 \(b_j\) 排序，则能转移到 \(f_i\) 的是 \(x_i\) 类的一段前缀。

注意到 \(w(j,i)=g(b_j,a_i)\times t_{bel}\) 满足四边形不等式，因为 \(g\) 满足，乘上常数也满足。

使用二分队列优化，每次转移 \(f_i\)，并加入决策点 \(i\)。

时间复杂度 \(\mathcal O(n\log^2n)\)。

P8290 [省选联考 2022] 填树

给你一棵 \(n\) 个节点的树，每个点 \(i\) 可以填一个 \([l_i,r_i]\) 的权值，也可以不填，现在我们要填一条树上路径，要求这条路径上的权值极差在 \(k\) 以内，问有多少种方案以及所有方案的权值和为多少。

\(n\le 200,1\le k\le 10^9,1\le l_i\le r_i\le 10^9\)。

---

枚举最小值，钦定权值在 \([L,L+k]\) 之中，为了防止重复需要存在值为 \(L\)，只需减去 \([L+1,L+k]\) 的方案。

答案为 \(\sum_{w}f_{w,w+k}-f_{w+1,w+k}\)。

固定区间后的答案容易计算，枚举链 LCA 做树上统计，单次复杂度 \(\mathcal O(n)\)。

发现当询问端点 \(L,R\) 与 \(l_i,r_i\) 相对顺序不变时，每个点合法性不变，且若合法，可填权值为一次函数。

则此时答案可以表示为 \(\mathcal O(n)\) 次多项式，分别为方案数前缀和多项式与权值和前缀和多项式。

为了避免卷积，我们代入 \(\mathcal O(n)\) 个值求解，单次复杂度 \(\mathcal O(n^2)\)。

而相对顺序只会变化 \(\mathcal O(n)\) 次，对每一段分别求解即可做到 \(\mathcal O(n^3)\)。

二分队列

可以解决在线的决策单调性，要求转移系数可以快速计算。

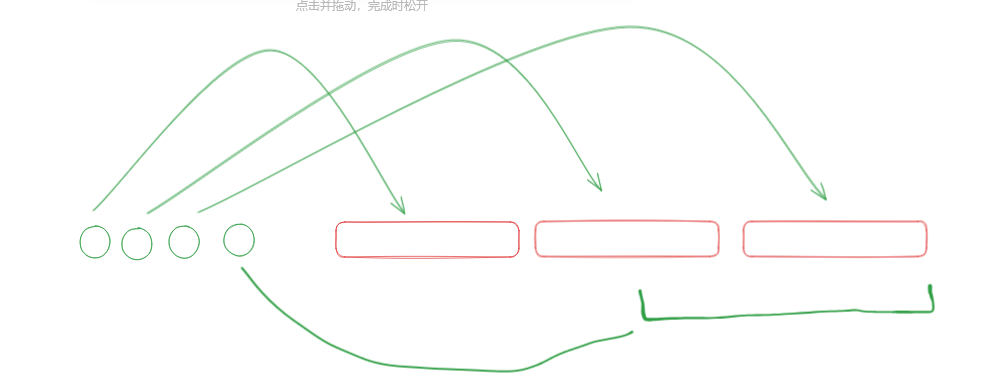
具体地，从前往后加入决策点，维护 \((i,l,r)\) 表示当前 \([l,r]\) 的最优决策点为 \(i\)，队列中的决策点为一段前缀，转移点为一段后缀。

加入决策点 \(i\) 后，修改队列头的分界线，找到 \(i\) 的最优决策点，计算出 \(f_i\)。

再考虑它作为决策点的贡献：它会作为一段后缀的最优决策点，这段后缀可以分成若干整段与一个散段。

则不断弹出整段，在最后一个段中二分分界线即可。

二分栈

适用于 \(w(j,i)\) 满足反四边形不等式的在线决策单调性。

反四边形不等式：即包含优于相交，此时决策点满足不会相交。

与上面类似。

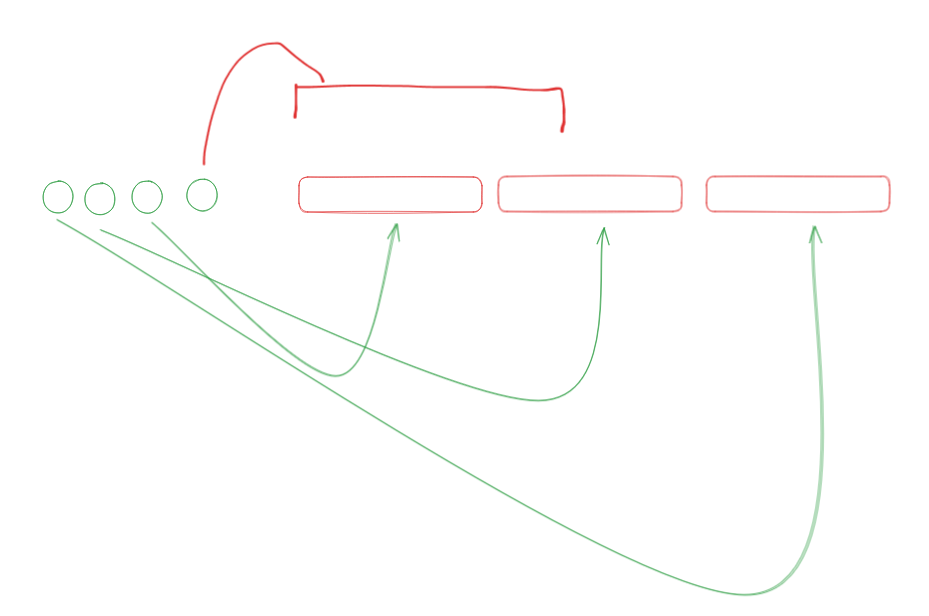
从前往后加入决策点，维护 \((i,l,r)\) 表示当前 \([l,r]\) 的最优决策点为 \(i\)，队列中的决策点为一段前缀，转移点为一段后缀。

加入决策点 \(i\) 后，修改队列尾的分界线，找到 \(i\) 的最优决策点，计算出 \(f_i\)。

再考虑它作为决策点的贡献：它会作为一段前缀的最优决策点，这段后缀可以分成若干整段与一个散段。

则不断弹出整段，在最后一个段中二分分界线即可。

望春风(see)

黑板上有若干个数，每次你可以选择 \(x,y\)，写下 \(\frac{x+y}{2}\)，要求 \(2|(x+y)\)。

给你序列 \(a\)，每次对 \(a\) 的一个区间询问总共能写下多少数。

\(n\le 5\times 10^5,q\le 3\times 10^6\)。

---

显然最小最大值不会变化。

考虑答案序列的相邻差，显然 \(2\nmid d_i\)。

且 \(d_i=d_{i+1}\)，否则可以新增中点。

那么说明结果为等差数列，考虑求公差，发现其为 \(\gcd\) 取出二进制末尾 \(0\)。

是是非非(yes)

观察到若将颜色分为 \(A\)、\(B\) 类，可以求出限定关键点处于 \(A\) 类的方案数。

\[g_i=\sum_{j=0}^{i}\binom{i}{j}f_j \]

最后答案为 \(\sum_i \binom{m}{i}f_i i^k\)。

考虑拆开组合意义，从 \(i\) 种颜色选 \(k\) 次的方案数。

枚举选 \(k\) 次后本质不同为 \(j\) 种，求出“选”的方案数（对着 \(i^k=\sum_{j=0}^{i}\binom{i}{j}coef_j\)），再求出染色对应的方案数（现在是要求关键点包含若干颜色，正难则反，容斥钦定 \(j\) 种没有出现过，则关键点只能在 \(m-j\) 种里选：\(h_i=\sum_{j=0}^{i}(-1)^j\binom{i}{j}g_{m-j}\) 即可。

---

但其实核心思想是已知 \(g\) 为 \(f\) 的高维前缀和，现在要求 \(\sum \binom{m}{i}f_i i^k\)。

对 \(i^k\) 进行第二类斯特林数拆分，拆到 \(1\sim \min(m,k)\) 中，对 \(j\) 求高维后缀和，实际意义为求关键点包含 \(j\) 种颜色的方案数，再容斥使得只需枚举 \(\le k\) 的下标。

流沙(sand)

将所有点放在平面上，实际上两种操作分别是选择两个点，\(x\) 交换，或者 \(y\) 交换，代价为总移动距离 \(/2\)。

不妨考虑一组起点终点匹配，则代价为曼哈顿距离 \(/2\)。

猜测存在操作可以取到下界，则后面就是使用流求解。

证明：对于这个构造两维是独立的，等价于有排列 \(p\)，每次花费 \(|i-j|\) 代价交换 \(p_i,p_j\)，求 \(p_i=i\) 的最小代价，答案就是 \(\frac{\sum|i-p_i|}{2}\)。

相当于证明操作操作的交换方向是固定的。

每次选择最小的 \(p_i\ne i\)，再找到 \(p_j=i\)，则 \(p_i,p_{i+1},\dots,p_{j-1}\) 这一定存在数 \(\ge j\)（根据抽屉原理），找到这个位置交换即可。

另一道题：2024 省集

前缀和与差分(coprime)

令 \(f_i\) 表示 \([1,i]\) 的序列答案和，令 \(g_i\) 表示 \([1,i]\) 的 \(\gcd =1\) 的序列个数。

\[f_i=\sum_{\gcd}\gcd^2 g(\lfloor\frac{i}{\gcd}\rfloor)\\ g_i=\sum_p \mu(p)(\lfloor\frac{i}{p}\rfloor)^n \]

对 \(g_i\) 增量，改变的只有 \(i\) 的因子。

只看改变的转移，是狄利克雷卷积，且其中一维是积性函数，可以类似埃氏筛枚举质数，将质数卷上去，时间复杂度 \(\mathcal O(n\log\log n)\)。

而 \(f\) 的转移也是一样的。

二分(binary)

先考虑求子集的二分边子图个数。

枚举一种染色方案，则符合这种方案的边集为 \(2^{cross(S,T)}\)。

对于一个二分边集，若其有 \(k\) 个弱连通块，则他被计数了 \(2^k\) 次。

令 \(f_s\) 表示 \(s\) 子集的二分边子图（导出子图联通）个数 \(\times 2\)，\(g_s\) 表示 \(s\) 子集的二分边集（点集恰为 \(s\)，可以不联通）。

则 \(g=e^f\)，对于 \(g\) 的转移式子很好列，可以优化成子集卷积的形式，最后得到 \(f\)。

最后再令 \(h_{s,j}\) 表示 \(s\) 子集，分成 \(j\) 个的弱联通块（每个二分）的方案数，转移需要枚举子集。

考虑优化，其实你只需要用到 \(h_U\) 的值，故我可以钦定一种转移顺序，每次只转移最高位的 \(0\) 对应的集合。

则对于 \(h_{s,j}\)，其高 \(j\) 位都被填了，枚举 \(s\) 的最高 \(0\) 位以及对应 \(s\)，转移就是取出能转移的东西做子集卷积。

时间复杂度 \(O(\sum 2^jj^2)=O(2^nn^2)\)。

逆序对(count)

妙妙题。

对于 \(l+r\ne n+1\) 的操作，我们始终可以找到和他不同的对应操作，使得区间中逆序对只会在恰好一种情况贡献到。

则一种操作顺序只需在最紧处考虑，注意，当第一次达到最紧时，后面的操作变成另一种对应规则。

最后的总逆序对个数是好求的，区间中好求，前缀后缀不同，首尾与中间相对顺序不变。

再考虑加入 \(l+r=n+1\) 的操作，现在问题是没有与他匹配的操作。

考虑给加入匹配操作（对序列不操作），操作树产生变化。

需要求不存在新增操作的方案的逆序对数，钦定若干次为新增操作，由于新增操作不发生变化，只需要求其他操作任意即可，逆序对数是好求的。

最后列出式子使用组合数学优化即可。

时间复杂度 \(\mathcal O(n\log n)\)。

CF2164

P14480 化作彗星

灵机一动就想到了。

首先当 \(s,t\) 是否有合法边的状态不同时，无解。

然后我们可以通过一条边让一个点变成：

• 若其在二分连通块内：变成同颜色的点。
• 否则可以变成块内任意点。

当图连通时，序列顺序可以任意交换，合法条件为：若是二分图，对应颜色点数量相同；否则始终合法。

当图任意时，一个想法是对相同连通块的段考虑，找到所有可以成为匹配的匹配起来，这些东西可以变成任意匹配（匹配定义为：若是二分图，颜色不同；否则任意情况都行），剩下的东西的相对顺序无法变化。

最后对 \(s,t\) 都跑一遍这个处理，合法条件是匹配数量相同，剩下东西对应相同。

文件资源管理器

https://ac.nowcoder.com/discuss/1581956

积木坐飞机

小吃街(food)

CF1994H Fortnite

跳跃(jump)

P9999 [Ynoi2000] tmostnrq2

P14462 【MX-S10-T3】『FeOI-4』寻宝游戏

P14463 【MX-S10-T4】『FeOI-4』呼吸之野

sb CF H2 slope trick

P14522 【MX-S11-T3】空之碎物

Stack(Stack)

String(String)

CF2165