11.4多校联训
T1 构造(ryx)
Sol
先考虑如何构造能最大化ryx个数:因为y在最终间,几次尝试后发现当数列为\(ryxy\)重复的时候答案最优。如此可以构造出一个40×40的矩阵,这个矩阵中ryx的个数为\((3*40-2)*(10*2-1)=2204\)。然而不难发现,最后一列全部是y,对答案没有贡献,考虑将横排的填法竖着在做一次,可以得到类似下面的矩阵:
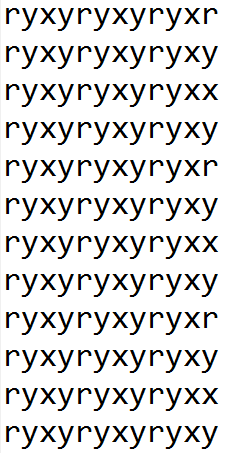
这样最后一列也能给予19的贡献,总计\(2223\),就已经达到了题目要求的上限了。
然后就是处理不满的时候的细节:考虑横排的每个点对答案的贡献:y显然没有贡献;r和x贡献都是正左、左上、右上,为3;而最左边的r只有1贡献,最右边的x只有2贡献。计算完每个点的贡献以后就可以来看怎么处理边界的点了:首先前面整行的点计算公式是\((3x-2)*19\),先确定有多少行是全部按照上面的填法填的。然后求出还剩下多少个\(ryx\),下面一行暴力枚举每个点贡献:如果贡献加上以后没有超过限制,就照常输出;否则剩下的全部输出y防炸,在最后一列上把剩下的输出出来即可,很容易证明不会有多出来的ryx。
Code
<-To Be Continued
T2 游戏(game)
Sol
我是傻逼。题都读不懂。
假设现在这个学生每间教室有\(b_i\)的概率去,那么老师的最佳方案就是$$\max _{i=1} ^n a_i*(1-b_i)$$,现在要确定每个\(b_i\),使得这个式子最小,二分答案即可。时间复杂度\(O(n*log\ 4e10)\)
Code
#include<bits/stdc++.h>
using namespace std;
int n;const int maxn=31;
double a[maxn];
int main()
{
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf",&a[i]);
double l=0,r=40;
while(r-l>0.0000000001)
{
double mid=(l+r)/2,cnt=0;
for(int i=1;i<=n;i++)
{
if(mid>=a[i])continue;
cnt+=1.0-mid/a[i];
}
if(cnt>1)l=mid;
else r=mid;
}
printf("%.10lf\n",l);
return 0;
}
T3 数数(count)
Sol
只会暴力。
T4 滈葕(dopetobly)
Sol
题解写的是2-SAT,没搞懂。。。
结论:一个点能填C就填C,不然能填D就填D,这样一定最优。
证明:显然C和D的功能强于A和B,所以只要CD填的越多后面限制条件就越少。
对于一条边\((x,y,z)\),若\(z=1\),那么\(x\)不可能填D,\(y\)不可能填C。
第一次建图:把所有以可能填C的点为起点,边权为\(0\)的边加进来跑dfs,如果一条边的终点不能填C,那么这条边的起点也不能。证明显然;
第二次建图:把所有已可能填D的点为终点,边权为\(0\)的边建反图,和第一次建的一样跑就行了。
第三次建图:把剩下没标上号的点建成双向边,然后黑白染色。边权为1就取反,为0就去相同。遇到不合法就输出NO。最后标完输出即可。
Code
#include<bits/stdc++.h>
using namespace std;
namespace io
{
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=0;c=getchar();}
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c&15),c=getchar();
return f?x:-x;
}
inline void print(int x)
{
static int s[20],len;
len=0;
if(x<0)putchar('-'),x=-x;
if(x==0)
{
putchar('0');return;
}
while(x)
{
s[++len]=x%10;
x/=10;
}
for(int i=len;i;i--)putchar(s[i]+'0');
return;
}
}
using namespace io;
const int maxn=100010,maxm=500010;
struct edge
{
int to,next,v;
}e[maxm<<1];
int h[maxn],ei;
inline void add(int x,int y,int v)
{
e[++ei]=(edge){y,h[x],v};
h[x]=ei;return;
}
int clr[maxn],n,m,len;
bool falg[maxn],fgla[maxn];//能否为C/D
int frm[maxm],t[maxm],val[maxm];
bool vis[maxn];
inline bool dfs(int x)
{
vis[x]=1;
for(int i=h[x];i;i=e[i].next)
{
int to=e[i].to;
if(vis[to]&&falg[to]==0)continue;
if(falg[to]||dfs(to)==0)
{
falg[x]=1;
return 0;
}
}
clr[x]=3;return 1;
}
inline bool dfs1(int x)
{
vis[x]=1;
for(int i=h[x];i;i=e[i].next)
{
int to=e[i].to;
if(vis[to]&&fgla[to]==0)continue;
if(fgla[to]||dfs1(to)==0)
{
fgla[x]=1;
return 0;
}
}
clr[x]=4;return 1;
}
inline bool dfs2(int x,int nowc)
{
clr[x]=nowc;
for(int i=h[x];i;i=e[i].next)
{
int to=e[i].to;
if(clr[to])
{
if(clr[to]!=((clr[x]-1)^e[i].v)+1)return 1;
continue;
}
if(dfs2(to,((nowc-1)^e[i].v)+1))return 1;
}
return 0;
}
int main()
{
freopen("dopetobly.in","r",stdin);
freopen("dopetobly.out","w",stdout);
n=read();m=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),z=read();
if(x==y)
{
if(z==1)
{
printf("NO\n");return 0;
}
continue;
}
if(z==1){fgla[x]=1;falg[y]=1;}
frm[++len]=x;t[len]=y;val[len]=z;
}
for(int i=1;i<=len;i++)
{
int x=frm[i],y=t[i],z=val[i];
if(z)continue;
if(falg[x]==0)add(x,y,z);
}
for(int i=1;i<=n;i++)
{
if(clr[i]==0&&falg[i]==0)dfs(i);
}
memset(h,0,sizeof(h));ei=0;
memset(vis,0,sizeof(vis));
for(int i=1;i<=len;i++)
{
int x=frm[i],y=t[i],z=val[i];
if(z)continue;
if(fgla[y]==0)add(y,x,z);
}
for(int i=1;i<=n;i++)
{
if(clr[i]==0&&fgla[i]==0)dfs1(i);
}
memset(h,0,sizeof(h));ei=0;
memset(vis,0,sizeof(vis));
for(int i=1;i<=len;i++)
{
int x=frm[i],y=t[i],z=val[i];
if(clr[x]||clr[y])continue;
add(x,y,z);add(y,x,z);
}
for(int i=1;i<=n;i++)
{
if(!clr[i])
{
if(dfs2(i,1))
{
printf("NO\n");return 0;
}
}
}
printf("YES\n");
for(int i=1;i<=n;i++)
{
if(clr[i]==1)putchar('A');
else if(clr[i]==2)putchar('B');
else if(clr[i]==3)putchar('C');
else if(clr[i]==4)putchar('D');
else putchar('!');
}
putchar('\n');
return 0;
}
另:数据出锅了我不知道,对着一份正确的代码调半天/kk



 浙公网安备 33010602011771号
浙公网安备 33010602011771号