Tarjan算法和强连通分量

强连通与强连通分量

• 强连通：若一张有向图的节点两两互相可达，则称这张图是强连通的。
• 强连通分量（Strongly Connected Components, SCC）：极大的强连通子图。
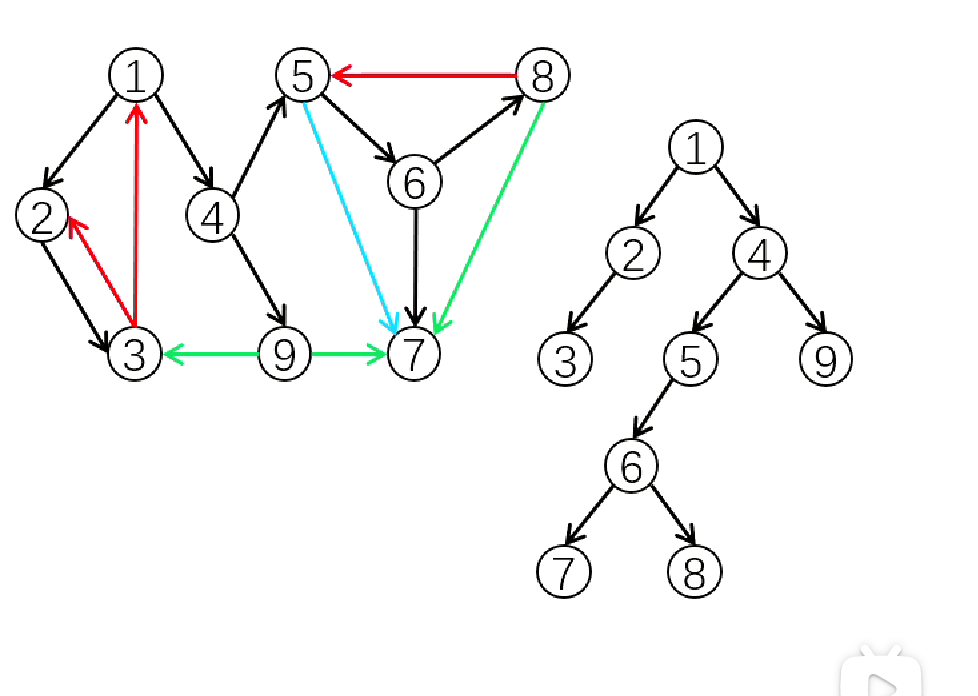
  例如，图中的SCC：(1) 1,2,3,4,9 (2) 5,6,8 (3) 7

搜索树

对图深搜时，每一个节点只访问一次，被访问过的节点与边构成搜索树。

有向边的分类（按访问情况分4类）

1. 树边（tree edge）：访问节点走过的边。图中的黑色边。
2. 返祖边（back edge）：指向祖先节点的边。图中的红色边。
3. 横叉边（cross edge）：右子树指向左子树的边。图中的绿色边。
4. 前向边（forward edge）：指向子树中节点的边。图中的蓝色边。

边的性质

返祖边与树边必构成环，横叉边可能与树边构成环。前向边无用。

如果节点 ( x ) 是某个强连通分量在搜索树中遇到的第一个节点，那么这个强连通分量的其余节点肯定是在搜索树中以 ( x ) 为根的子树中。节点 ( x ) 被称为这个强连通分量的根。

Tarjan（塔扬）算法

核心概念

1. 时间戳 dfn[x]：节点 x 第一次被访问的顺序。
2. 追溯值 low[x]：从节点 x 出发，所能访问到的最早时间戳。

算法步骤

1. 入 x 时：为 x 分配时间戳（盖戳），并将 x 入栈。

2. 枚举 x 的邻点 y，分三种情况处理：
   (1) 若 y 尚未访问：
   对 y 进行深度搜索；回到 x 时，用 low[y] 更新 low[x]。
   （因为 x 是 y 的父节点，y 能访问到的点，x 一定也能访问到）
   (2) 若 y 已访问且在栈中：
   说明 y 是祖先节点或左子树节点，用 dfn[y] 更新 low[x]。
   (3) 若 y 已访问且不在栈中：
   说明 y 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

3. 离 x 时：记录强连通分量（SCC）。只有遍历完一个 SCC，才可以出栈。

   • 更新 low 值的意义：避免 SCC 的节点提前出栈。

点击查看代码

struct SCC {
    int n, cnt, idx;
    vi stk, instk;
    vi dfn, low, scc, siz;
    vvi g;
    SCC() {};
    SCC(int _n) {init(_n);}
    void init(int _n) {
        this -> n = _n;
        g.assign(_n + 1,vi());
        instk.resize(_n + 1);
        dfn.resize(_n + 1);
        low.resize(_n + 1);
        scc.resize(_n + 1);
        siz.resize(_n + 1);
        idx = cnt = 0;
    }
    void add(int u, int v) {
        g[u].emplace_back(v);
    }
    void tarjan(int u) {
        dfn[u] = low[u] = ++idx;
        stk.emplace_back(u),instk[u] = 1;
        for(auto v : g[u]) {
            if(!dfn[v]) {
                tarjan(v);
                low[u] = min(low[u], low[v]);
            } else if(instk[v]) {
                low[u] = min(low[u], dfn[v]);
            }
        }

        if(dfn[u] == low[u]) {
            int y;++cnt;
            do {
                y = stk.back();instk[y] = 0;
                scc[y] = cnt;
                stk.pop_back();
                siz[cnt]++;
            } while(y != u);
        }
    }
    void work() {
        for(int i = 1; i <= n; i++) {
            if(!dfn[i]) tarjan(i);
        }
    }
};