数据结构与算法（十）——堆

一、概述

1、介绍

　　堆：是具有以下性质的完全二叉树，建堆的时间o(n)。
　　大顶堆：根结点 >= 左右孩子结点，左右孩子不要求。
　　小顶堆：根结点 <= 左右孩子结点，左右孩子不要求。

　　大顶堆：

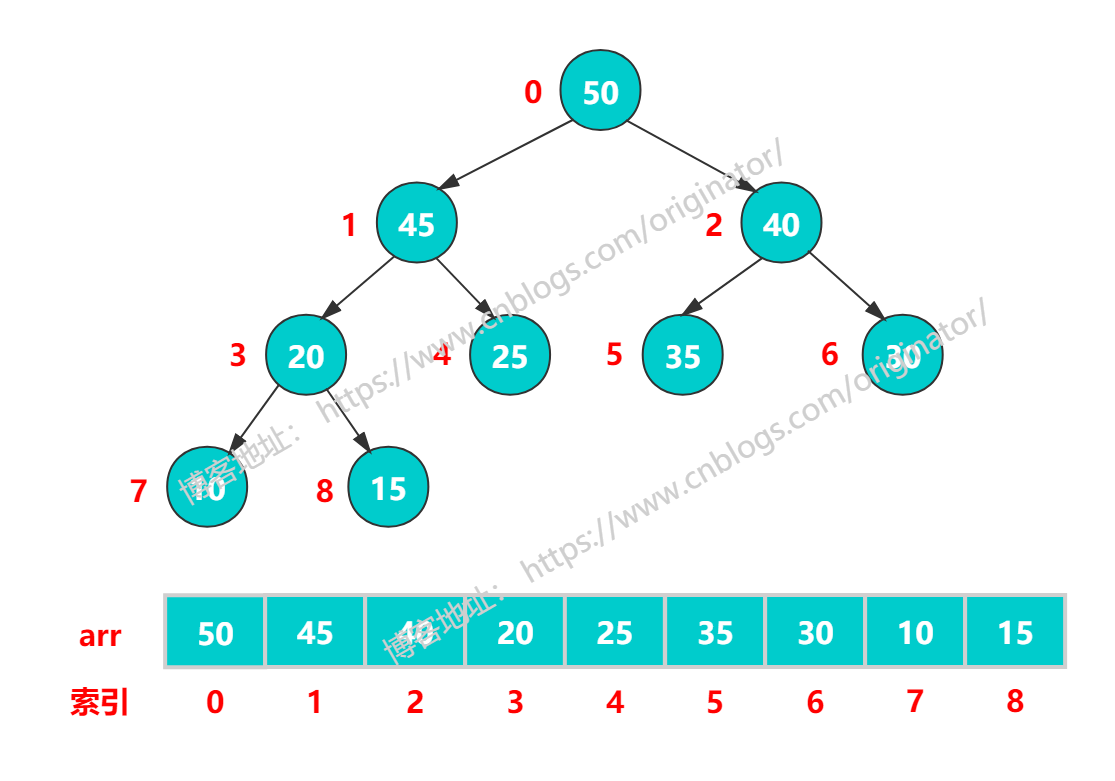
　　小顶堆：

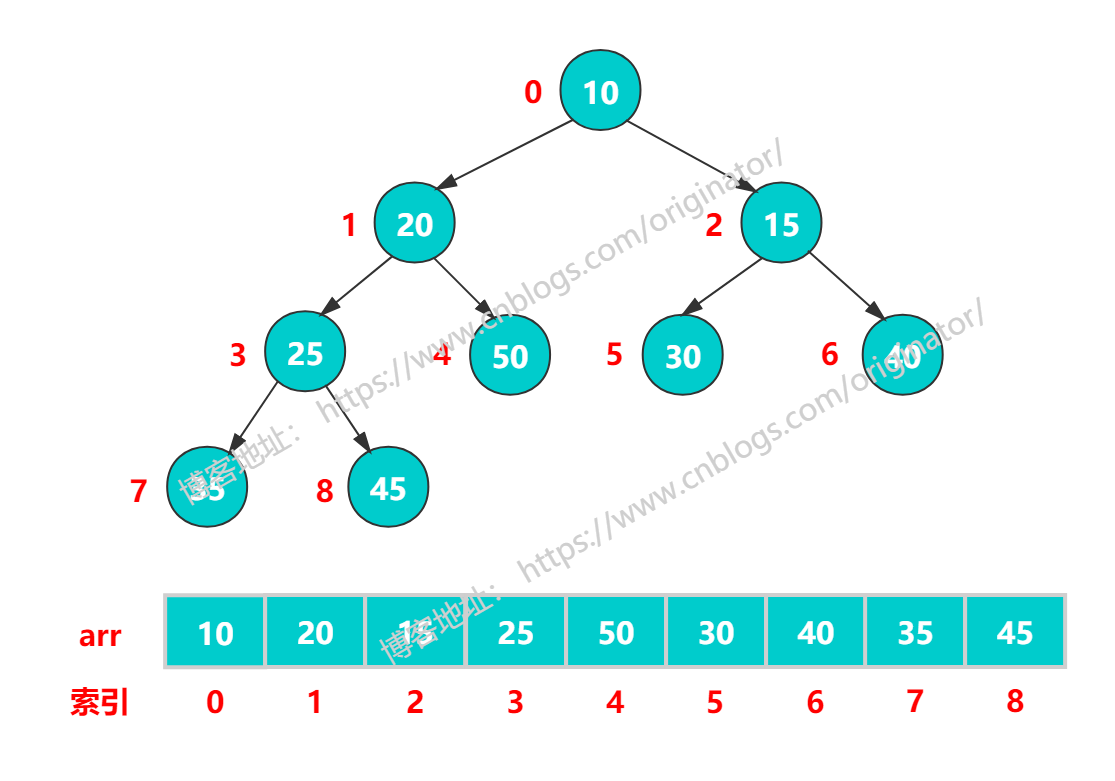
　　性质：由于堆是完全二叉树，对任意结点 i 左孩子是 2i + 1，右孩子是 2i + 2，则：
　　①大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
　　②小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
　　③最后一个非叶子结点：arr.length / 2 - 1

2、建堆过程

　　用数组 {4, 6, 8, 5, 9} 构建成一个大顶堆，从最后一个非叶子结点（6）开始倒着调整。如图：

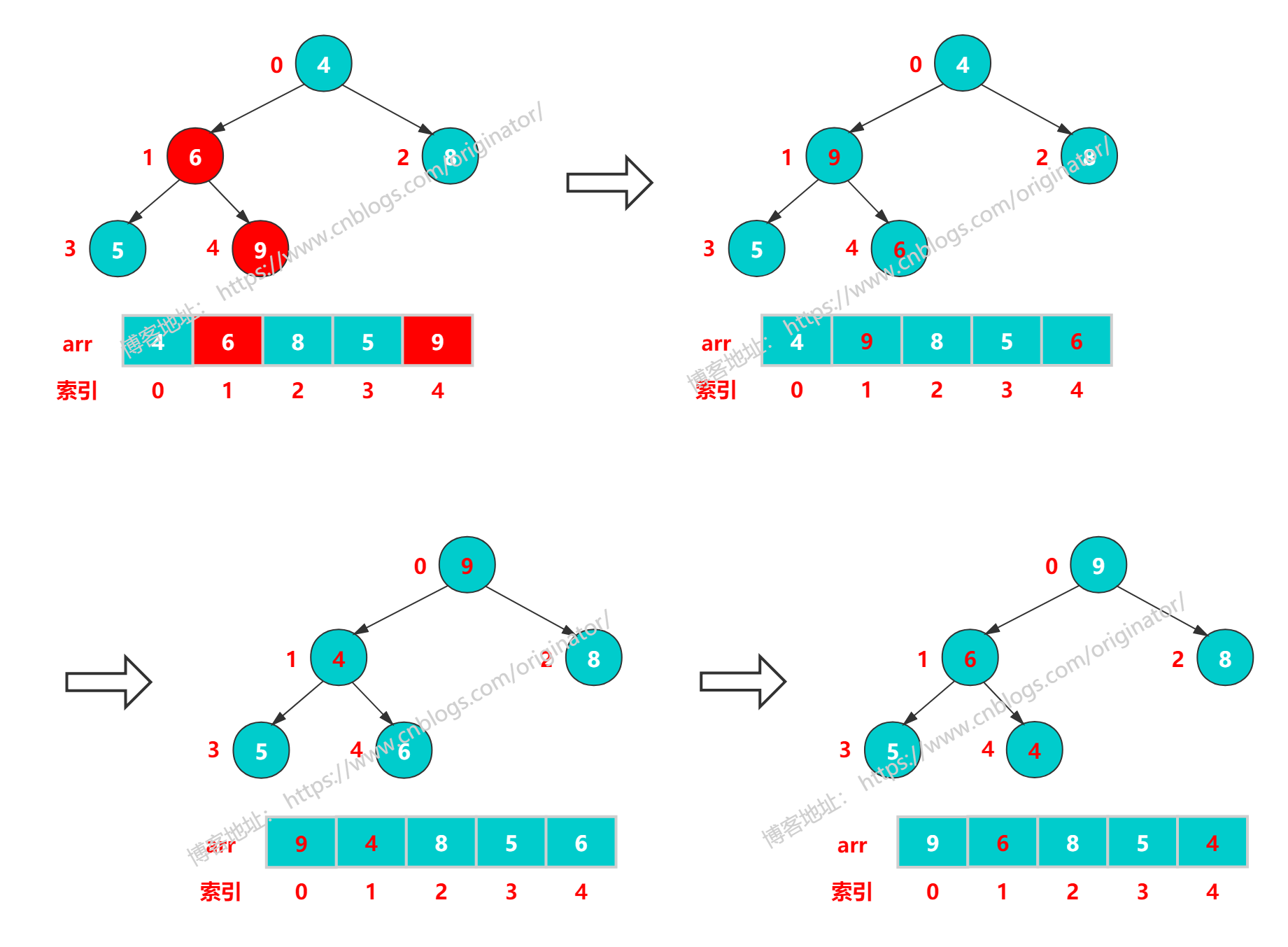
二、堆排序

1、介绍

　　堆排序是利用堆这种数据结构而设计的一种排序算法，是一种不稳定的选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)。

2、思想

　　（1）将待排序数组构建成一个大顶堆，自然有，arr[0] = max{arr}。
　　（2）将堆顶元素（最大）与数组的末尾元素交换，此时末尾元素就是最大值。
　　（3）将剩余的 n - 1 个序列重新调整成一个大顶堆，这样就得到 n 个元素中的次大值。
　　（4）如此反复，便能得到一个有序序列了。

3、过程

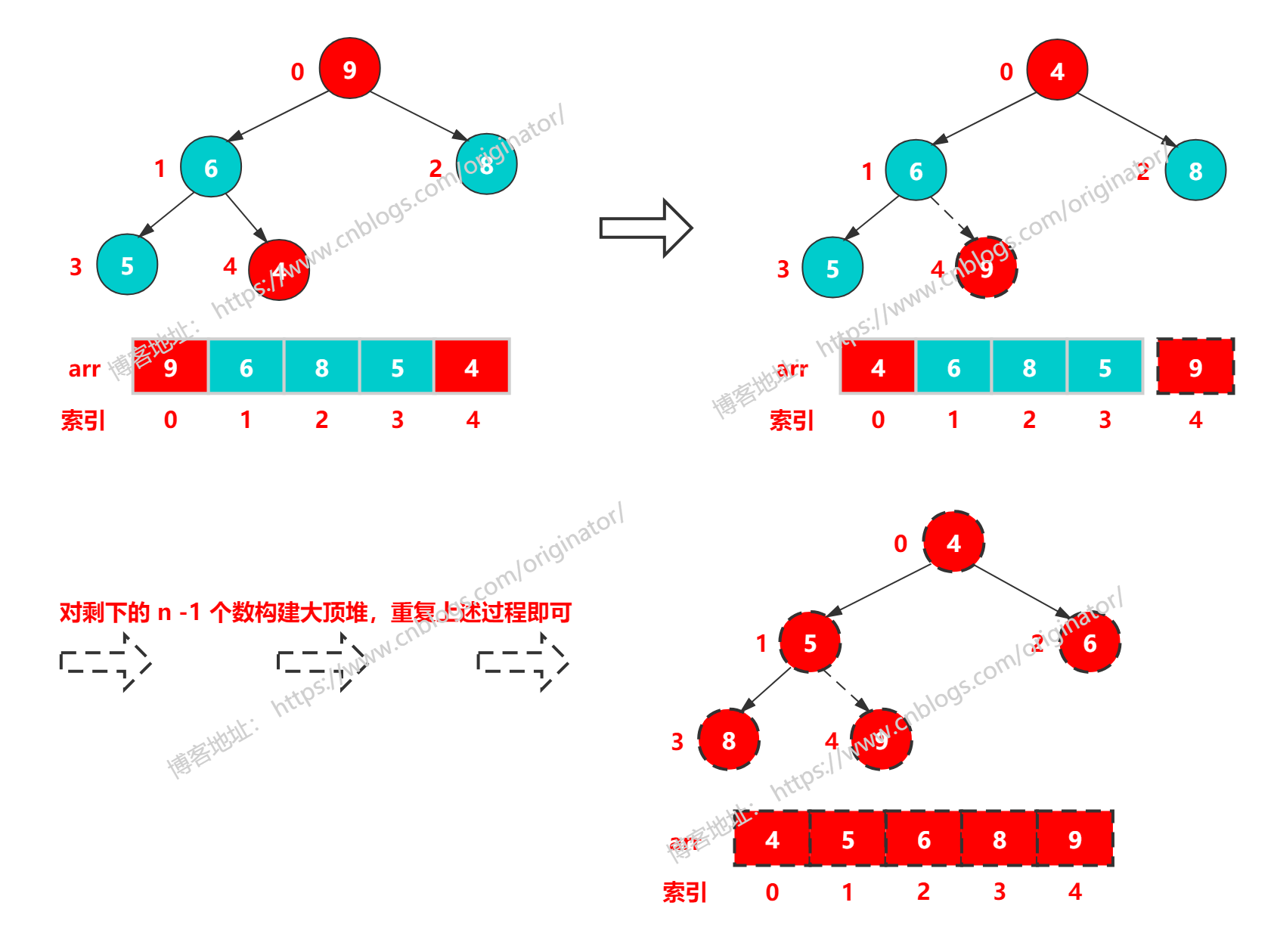
4、代码

// 堆排序
public static void heapSort(int[] arr) {
    // 1.构建大顶堆
    for (int i = arr.length / 2 - 1; i >= 0; i--) {
        adjustHeap(arr, i, arr.length);
    }

    // 2.交换.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端.
    for (int i = arr.length - 1; i > 0; i--) {
        swap(arr, 0, i);
        adjustHeap(arr, 0, i);
    }
}

/**
 * 调整堆，以 i 对应的非叶子结点的树调整为大（小）顶堆
 *
 * @param arr    待调整的数组
 * @param i      待调整的非叶子结点（数组的下标）
 * @param length 剩下的 length 个元素继续调整，每次length会逐渐减少
 */
private static void adjustHeap(int[] arr, int i, int length) {
    // k 是 i 的左孩子.存在
    for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
        // k+1 是 i 的右孩子.存在
        if (k + 1 < length && arr[k] < arr[k + 1]) {
            k++;
        }

        if (arr[i] >= arr[k]) {
            break;
        }

        swap(arr, i, k);

        // 继续调整因交换引起的孩子结点不满足堆的情况
        i = k;
    }
}

private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

5、小结

　　堆排序升序排序：大顶堆
　　堆排序降序排序：小顶堆
　　堆排序的时间复杂度是o(nlogn)
　　堆排序的空间复杂度是o(1)
　　构建堆的时间复杂度是o(n)
　　堆排序是一种不稳定的排序算法
　　有一组数据（15,9,7,8,20,-1,7,4），用堆排序的筛选方式建立的初始堆为（-1,4,7,8,20,15,7,9）。
　　将数组（7,6,3,5,4,1,2）按照堆排序的方式升序排序，则第一轮排序结束后，数组顺序是（6,5,3,2,4,1,7）。
　　对于根元素为最小值的二叉堆。
　　　　插入结点的复杂度是o(logn)
　　　　删除最小元素的复杂度是o(logn)（删除之后需要调整堆）
　　　　查询最小元素的复杂度是o(1)
　　有 n 个元素的序列，若使用筛选法建堆，则从位置为n/2取下整的元素开始建堆。
　　哈弗曼树带权路径长度最短的树，路径上权值较大的结点离根较近。
　　当从一个最小堆中删除一个元素时，需要把堆尾元素填补到堆顶位置，然后再按条件把它逐层向下调整到合适位置。

三、堆的应用

1、PriorityQueue优先队列

　　介绍：队列是遵循先进先出模式的，但有时需要在队列中基于优先级处理对象。就需要对象具有可比性；PriorityQueue是非线程安全的，所以Java提供了PriorityBlockingQueue（实现BlockingQueue接口）用于Java多线程环境。
　　代码示例：应用

// 优先队列
public class PriorityQueueDemo {
    public static void main(String[] args) {
        Queue<Stu> priorityQueue = new PriorityQueue<>();

        // 随机添加 7 个对象到队列中
        Random rand = new Random();
        for (int i = 0; i < 7; i++) {
            int id = rand.nextInt(100);
            priorityQueue.offer(new Stu(id, "Stu:" + id));
        }

        // 出队列
        while (!priorityQueue.isEmpty()) {
            final Stu stu = priorityQueue.poll();
            System.out.println(stu);
        }
    }
}
// 使对象具有可比性
class Stu implements Comparable<Stu> {
    private int id;
    private String name;

    public Stu(int id, String name) {
        this.id = id;
        this.name = name;
    }

    public int getId() {
        return id;
    }

    public void setId(int id) {
        this.id = id;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    @Override
    public int compareTo(Stu o) {
        return this.id - o.id;
    }

    @Override
    public String toString() {
        return "Stu{" +
                "id=" + id +
                ", name='" + name + '\'' +
                '}';
    }
}

　　底层实现原理：Java中 PriorityQueue 通过小顶堆实现。源码参看JDK源码。

2、top K

　　什么是 top K 问题？简单来说就是在一堆数据里面找到前 K 大（当然也可以是前 K 小）的数。
　　最直接的想法：先通过快排等算法将 n 个数排序，再取前 k 个。这种方式在数据量不大的时候可行，但固然不是最优的方法。比如在 1 亿个数中找前 10 大的数，将 1 亿个数都排序，未免有点浪费。
　　缺点：在海量数据下，很可能没办法一次性将数据全部加载入内存。

　　分布式思想处理海量数据：将数据分散在多台机器中，然后每台机器并行计算各自的 top K 数据，最后汇总，再计算得到最终的 top K 数据。

　　一台机器处理海量数据：堆排序。
　　思想：维护一个大小为 k 的小顶堆，从 i = k+1 开始遍历数组arr，如果 arr[i] > 堆顶元素，则用 arr[i] 替换堆顶元素，并重新调整堆使之为小顶堆。遍历完全部数据，堆里面就是top K。
　　直接使用优先队列 PriorityQueue 来实现一个小顶堆，求 top K 问题：

// top K
public List<Integer> solutionByHeap(int[] input, int k) {
    List<Integer> list = new ArrayList<>();
    if (k > input.length || k == 0) {
        return list;
    }

    Queue<Integer> queue = new PriorityQueue<>();
    for (int num : input) {
        if (queue.size() < k) {
            queue.offer(num);
        } else if (queue.peek() != null && queue.peek() < num) {
            // 堆顶元素出列
            queue.poll();
            queue.offer(num);
        }
    }

    while (!queue.isEmpty()) {
        list.add(queue.poll());
    }
    return list;
}