详解排序算法（二）之2种交换排序（冒泡排序、快速排序）

冒泡排序

所谓冒泡排序，就是相邻的两个元素相互比较并根据比较结果决定是否交换位置。如从小到大排序，相邻两个元素两两比较，将值更大的元素交换到右侧，如此到最后一个元素，就能确定最大的一个值，一轮排序结束。若某一轮排序交换位置的次数为0，则排序结束。

我们取 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 来进行示范

第一轮排序

  1. 3 与 44 比较 ，3 < 44 ，不变 ，得 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48

  2. 44 与 38 比较 ，44 > 38，44 与 38 交换，得 3, 38, 44, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48

  3. 44 与 5 比较 ，44 > 5 ，44 与 5 交换，得 3, 38, 5, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48

  4. 44 与 47 比较 ，44 < 47，不变 ，得 3, 38, 5, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48

  5. 47 与 15 比较 ，47 > 15，47 与 15 交换，得 3, 38, 5, 44, 15, 47, 36, 26, 27, 2, 46, 4, 19, 50, 48

  6. 47 与 36 比较 ，47 > 36，47 与 36 交换，得 3, 38, 5, 44, 15, 36, 47, 26, 27, 2, 46, 4, 19, 50, 48

  7. 47 与 26 比较 ，47 > 26，47 与 26 交换，得 3, 38, 5, 44, 15, 36, 26, 47, 27, 2, 46, 4, 19, 50, 48

  8. 47 与 27 比较 ，47 > 27，47 与 27 交换，得 3, 38, 5, 44, 15, 36, 26, 27, 47, 2, 46, 4, 19, 50, 48

  9. 47 与 2 比较 ，47 > 2，47 与 2 交换 ， 得 3, 38, 5, 44, 15, 36, 26, 27, 2, 47, 46, 4, 19, 50, 48

  10. 47 与 46比较 ，47 > 46，47 与 46 交换，得 3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 47, 4, 19, 50, 48

  11. 47 与 4 比较 ，47 > 4 ，47 与 4 交换 ，得 3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 47, 19, 50, 48

  12. 47 与 19 比较 ，47 > 19，47 与 19 交换，得 3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 50, 48

  13. 47 与 50 比较 ，47 < 50，不变 ，得 3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 50, 48

  14. 50 与 48 比较 ，50 > 48，50 与 48 交换，得 3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 48, 50

第一轮排序结束，交换位置次数：11

第二轮排序同理

当某一轮排序交换位置次数为 0，表明元素已满足从小到大排序，冒泡排序结束。

动态图

img

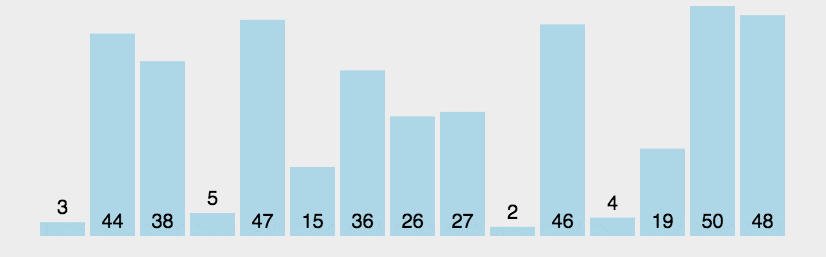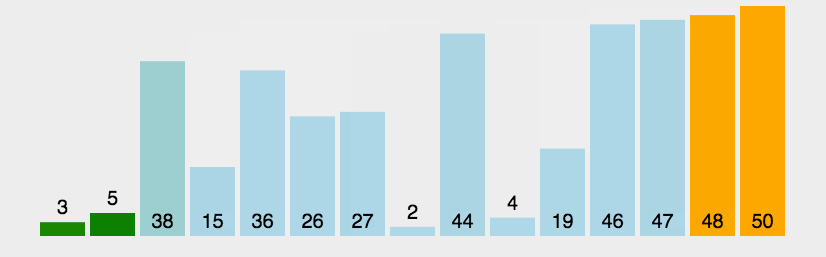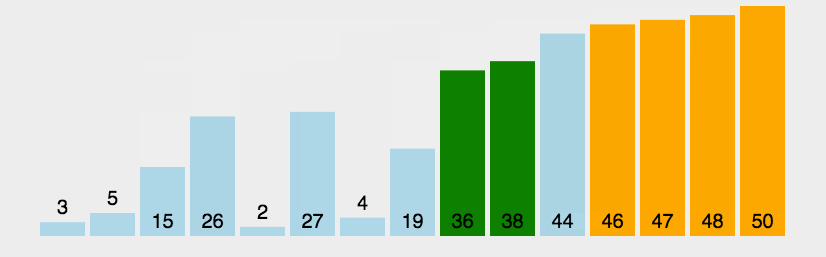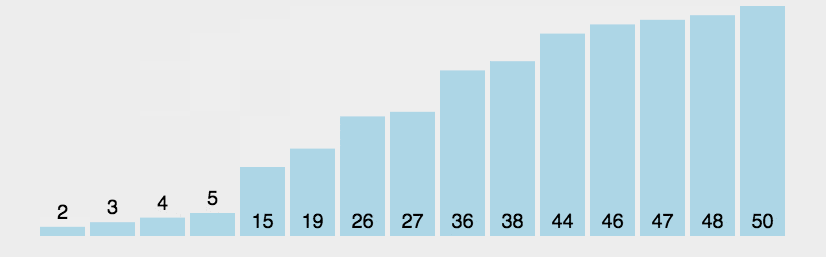
javascript代码

function bubbleSort(arr) {
    let count  // 一轮排序元素交换次数

    for (let i = 0; i < arr.length; i++) {
        count = 0

        for (let j = 1; j < arr.length - i; j++) {
            if (arr[j] < arr[j-1]) {
                temp = arr[j - 1]
                arr[j - 1] = arr[j]
                arr[j] = temp
                count++
            }
        }

        if (count === 0) break
    }

    return arr
}

快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。从本质上来看，快速排序是一种递归分治法。

算法步骤

  1. 从数列中挑出一个元素，称为 "基准"（pivot）;
  2. 将元素分而治之，小的置于基准值左侧，大的置于基准值右侧；
  3. 基准值两侧作为两个子数列，再分别找一个基准值，重复 步骤1。

我们仍取 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 来进行示范

第一轮排序

  1. 取基准值为 3
  2. 将 3 与 44, 38, 5, 47, 15, 36, 26, 27 比较，3比它们都小，位置保持不变
  3. 将 3 与 2 比较，3 > 2，2 与 44 交换位置，得 3, 2, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48
  4. 将 3 继续与 46, 4, 19, 50, 48比较，3比它们都小，位置保持不变
  5. 将 3 与 2 交换，得 2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48

可以发现，3 将数列分成了左右两部分子数列。再对子数列进行同样操作，即第二轮排序。

第二轮排序

  1. 左子数列只有一个元素，无需排序
  2. 右子数列取基准值为 38
  3. 38 > 5，5位置不变，得 2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48
  4. 38 < 47，位置不变，得 2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48
  5. 38 > 15，15 与 47 互换，得 2, 3, 38, 5, 15, 47, 36, 26, 27, 44, 46, 4, 19, 50, 48
  6. 38 > 36，36 与 47 互换，得 2, 3, 38, 5, 15, 36, 47, 26, 27, 44, 46, 4, 19, 50, 48
  7. 38 > 26，26 与 47 互换，得 2, 3, 38, 5, 15, 36, 26, 47, 27, 44, 46, 4, 19, 50, 48
  8. 38 > 27，27 与 47 互换，得 2, 3, 38, 5, 15, 36, 26, 27, 47, 44, 46, 4, 19, 50, 48
  9. 38 < 44, 46， 位置不变 ，得 2, 3, 38, 5, 15, 36, 26, 27, 47, 44, 46, 4, 19, 50, 48
  10. 38 > 4， 4 与 47 互换，得 2, 3, 38, 5, 15, 36, 26, 27, 4, 44, 46 , 47, 19, 50, 48
  11. 38 > 19，44 与 19 互换，得 2, 3, 38, 5, 15, 36, 26, 27, 4, 19, 46 , 47, 44, 50, 48
  12. 38 < 50, 48，位置不变 ，得 2, 3, 38, 5, 15, 36, 26, 27, 4, 19, 46 , 47, 44, 50, 48
  13. 将 38 与 19 交换，得 2, 3, 19, 5, 15, 36, 26, 27, 4, 38, 46 , 47, 44, 50, 48

可以发现，38 将右子数列又分成了左右两部分。再对子数列进行同样操作，即第三轮排序。

如此重复操作，直到分无可分，子数列元素个数为1时，排序结束。

动态图

img

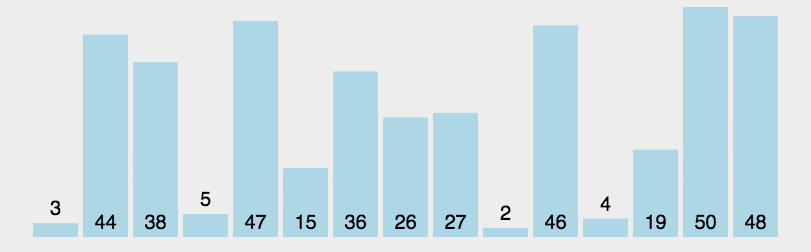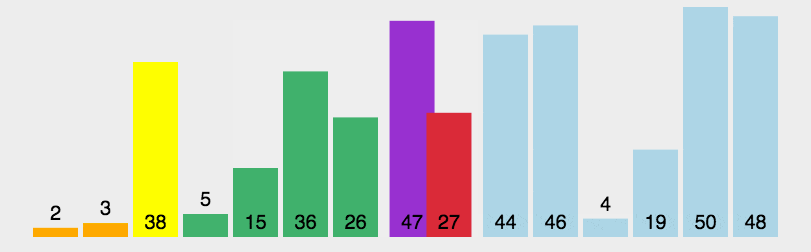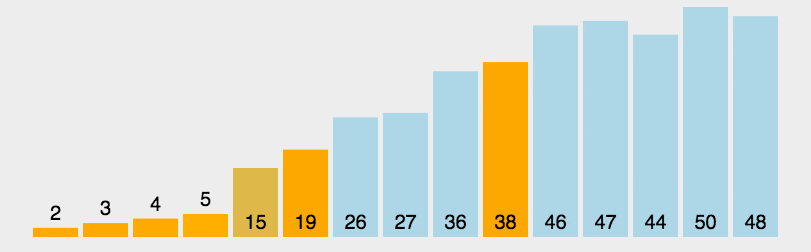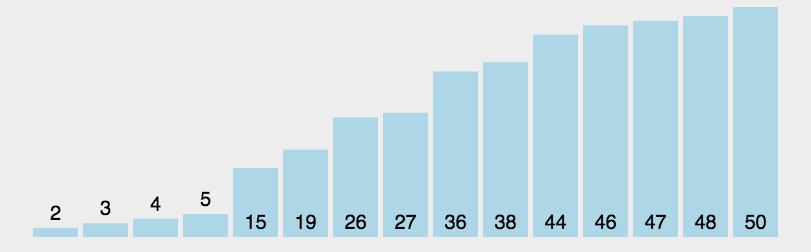
javascript代码

function quickSort(arr, low = 0, high = arr.length - 1) {
   if (low >= high) return

   const pivot = paritition(arr, low, high)

   quickSort(arr, low, pivot - 1)
   quickSort(arr, pivot + 1, high)

   return arr
}

function paritition (arr, low, high) {
    const pivot = arr[low] // 基准值
    let pivotIndex = low // 基准值最终位置

    for (let i = low; i <= high; i++) {
        if (arr[i] < pivot) {
            const temp = arr[i]
            arr[i] = arr[++pivotIndex]
            arr[pivotIndex] = temp
        }
    }

    arr[low] = arr[pivotIndex]
    arr[pivotIndex] = pivot

    return pivotIndex
}

除上面这种分割方式外，这里再介绍另一种快速排序的分割方式，那就是 严蔚敏《数据结构》标准分割函数

第一轮排序

  1. 取基准值为 3
  2. 从右向左（48开始） ，找到第一个小于 3 的值 2，交换 ，得 2, 44, 38, 5, 47, 15, 36, 26, 27, 3, 46, 4, 19, 50, 48
  3. 再从左向右（44开始），找到第一个大于 3 的值 44，交换，得 2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48
  4. 从右向左（27开始） ，未找到小于 3 的值 ，得 2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48

第二轮排序

  1. 左子数列只有一个元素，无需排序
  2. 右子数列取基准值为 38
  3. 从右向左（48开始），找到第一个小于 38 的值 19，交换 ，得 2, 3, 19, 5, 47, 15, 36, 26, 27, 44, 46, 4, 38, 50, 48
  4. 从左向右（5开始），找到第一个大于 38 的值 47，交换，得 2, 3, 19, 5, 38, 15, 36, 26, 27, 44, 46, 4, 47, 50, 48
  5. 从右向左（4开始） ，找到第一个小于 38 的值 4，交换 ，得 2, 3, 19, 5, 4, 15, 36, 26, 27, 44, 46, 38, 47, 50, 48
  6. 从左向右（15开始），找到第一个大于 38 的值 44，交换，得 2, 3, 19, 5, 4, 15, 36, 26, 27, 38, 46 , 44, 47, 50, 48
  7. 从右向左（46开始），未找到第一个小于 38 的值 ，得 2, 3, 19, 5, 4, 15, 36, 26, 27, 38, 46 ,44, 47, 50, 48

如此重复操作，直到分无可分，子数列元素个数为1时，排序结束。

javascript代码

function quickSort(arr, low = 0, high = arr.length - 1) {
    if (low >= high) return
 
    const pivot = paritition(arr, low, high)
 
    quickSort(arr, low, pivot - 1)
    quickSort(arr, pivot + 1, high)
 
    return arr
 }
 
 // 严蔚敏《数据结构》标准分割函数
 function paritition (arr, low, high) {
     const pivot = arr[low] // 基准值
 
     while (low < high) {
        while (low < high && arr[high] >= pivot) {
            high--
        }

        arr[low] = arr[high]

        while (low < high && arr[low] <= pivot) {
            low++
        }

        arr[high] = arr[low]
     }

     arr[low] = pivot

     return low
 }

两种算法的复杂度及稳定性

排序算法 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度 稳定性
冒泡排序 O(n2) O(n2) O(n) O(1) 稳定
快速排序 O(nlog2n) O(n2) O(nlog2n) O(log2n) 不稳定
posted @ 2022-03-08 21:40  Programing_Monkey  阅读(176)  评论(0)    收藏  举报