良心的前置知识点普及时间:(如果都会就跳到Task.1)(赶工暂时先假装没有这个东西)
Task.1 Count
题目大意:求方程:\(\sum^k_{i=1}a_i=n\quad(\forall a_i\quad a_i\nmid m)\)有多少组不同的解。
数据范围:\(N\leq 10^{18},m\leq 5000,k\leq 2000\)
这是什么,这是被容斥支配的恐惧
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
template<class T>void read(T &x){
x=0; char c=getchar();
while(c<'0'||'9'<c)c=getchar();
while('0'<=c&&c<='9'){x=(x<<1)+(x<<3)+(c^48); c=getchar();}
}
typedef unsigned long long ll;
const int N=5050;
const int M=998244353;
ll n,m,k;
int fac[N*N],inv[N*N],ifac[N*N];
ll C(ll x,ll y){
// printf("%d %d\n",x,y);
return x<y?0:1ll*fac[x]*ifac[y]%M*ifac[x-y]%M;
}
void init(){
fac[0]=fac[1]=inv[0]=inv[1]=ifac[0]=ifac[1]=1;
for(int i=2;i<=k*(m-1);i++){
fac[i]=1ll*fac[i-1]*i%M;
inv[i]=1ll*inv[M%i]*(M-M/i)%M;
ifac[i]=1ll*ifac[i-1]*inv[i]%M;
}
}
int main(){
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
read(n); read(m); read(k);
init();
ll s=n%m,t;// if(s<k)s+=m;
ll ans=0,sum,tmp,mul,rst;
for(;s<=min(k*(m-1),n);s+=m){
sum=C(s-1,k-1);
for(ll i=1;i*(m-1)<=s;i++){
t=s-i*(m-1);
tmp=1ll*C(t-1,k-1)*C(k,i)%M;
sum=i&1?(sum-tmp+M)%M:(sum+tmp)%M;
// printf("%c %lld * %lld",i&1?'-':'+',C(t-1,k-1),C(i+k-1,k-1));
}
// printf("= %lld\n",sum);
mul=ifac[k-1]; rst=(n-s)/m;
for(ll i=rst+k-1;i>=rst+1;i--)mul=mul*(i%M)%M;
// printf("%lld %lld %lld\n",s,sum,mul);
sum=(sum*mul)%M;
ans=(ans+sum)%M;
}
printf("%lld\n",ans);
return 0;
}
Task.2 普及组
题目大意:定义一个 \(n\times n\) 的矩阵 \(A\) 是好的当它满足:\(\forall A_{i,j} \in \mathbb{Z},\ \forall j \prod^n_{i=1}A_{i,j}=x,\ \forall i \prod^n_{j=1}A_{j,i}=x\)。给出 \(n,x\),求有多少个好的矩阵。 \(T\) 组询问,对 \(998244353\) 取模。
数据范围:\(0\leq T\leq 2\times 10^5,1\leq n\leq 5\times 10^6\)
这个范围非常的“提答”,不得不贴: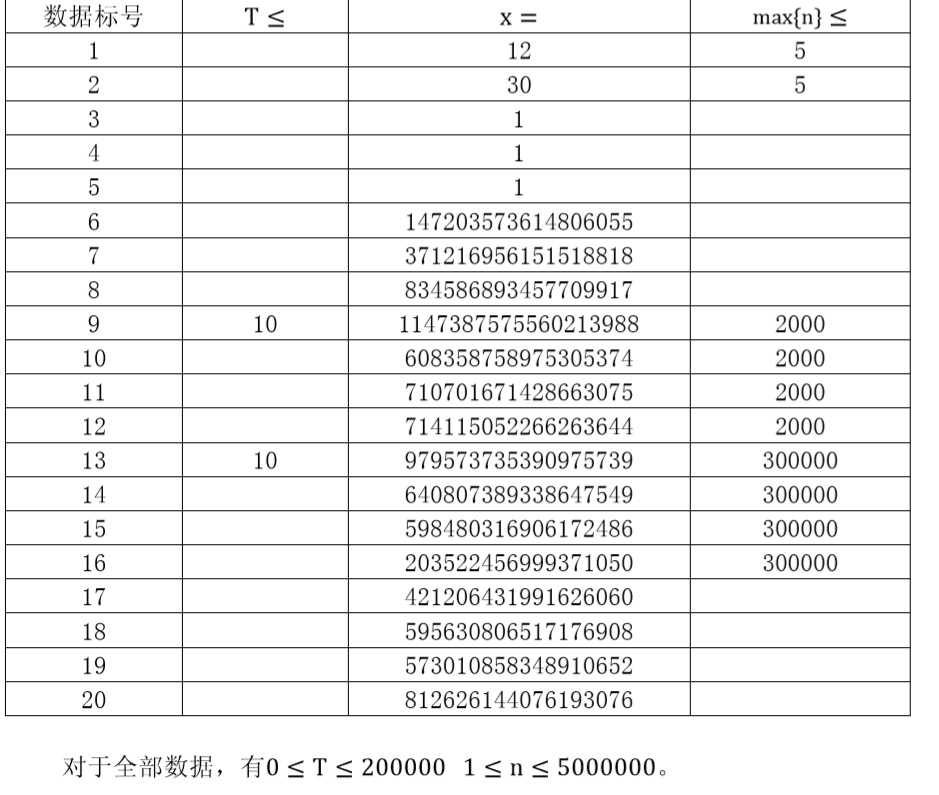
我们非常套路的分解个质因数看看,发现这些个看着渗人的 \(x\) 的质因子的次幂都不超过 \(2\)。
诶嘿嘿(我出去了)。
对于 \(x=1\) 的情况,
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
template<class T>void read(T &_){
_=0; char c=getchar();
while(c<'0'||'9'<c)c=getchar();
while('0'<=c&&c<='9'){_=(_<<1)+(_<<3)+(c^48); c=getchar();}
}
typedef long long ll;
const int N=5000005;
const int M=998244353;
int fac[N],f[N],g[N];
int qpow(int a,int b){
int tmp=1,base=a;
while(b){
if(b&1)tmp=(1ll*tmp*base)%M;
base=(1ll*base*base)%M; b>>=1;
} return tmp;
}
int main(){
freopen("pj.in","r",stdin);
freopen("pj.out","w",stdout);
int cp,c1=0,c2=0,i2=499122177;
ll x;
int T,n,t;
read(x); read(T);
for(int p=2;1ll*p*p<=x;p++){
if(x%p==0){
cp=0; while(x/p*p==x)x/=p,++cp;
(cp==1)?++c1:++c2;
}
} if(x>1)++c1;
fac[0]=fac[1]=g[1]=1;
for(int i=2;i<=5000000;i++){
fac[i]=1ll*fac[i-1]*i%M;
t=(f[i-1]+g[i-1]>=M)?(f[i-1]+g[i-1]-M):(f[i-1]+g[i-1]);
g[i]=1ll*t*i%M;
t=(t+f[i-1]>=M)?(t+f[i-1]-M):(t+f[i-1]);
f[i]=1ll*t*i%M*(i-1)%M*i2%M;
}
while(T--){
read(n); t=(f[n]+g[n]>=M)?(f[n]+g[n]-M):(f[n]+g[n]);
printf("%d\n",1ll*qpow(fac[n],c1)*qpow(t,c2)%M*qpow(2,1ll*(n-1)*(n-1)%(M-1))%M);
}
return 0;
}
Task.3 提高组
题目大意:定义一个长度为 \(n\) 的正整数序列 \(A\) 是好的当:\(\forall A_i\ 1\leq A_i\leq n,\ i\neq j\Leftrightarrow A_i\neq A_j\),最长下降子序列长度不超过 \(2\)。\(T\) 组询问,每次查询满足 \(A_x=y\) 的长度为 \(n\) 的好的序列有多少个,答案对 \(10^9+7\) 取模。
数据范围:\(0\leq T\leq 10^6,1\leq N\leq 10^7\)
题目那么长其实简单说就是求最长下降子序列长度不超过 \(2\) 的满足条件的排列有多少(害我打题目打这么久)
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
template<class T>void read(T &x){
x=0; char c=getchar();
while(c<'0'||'9'<c)c=getchar();
while('0'<=c&&c<='9'){x=(x<<1)+(x<<3)+(c^48); c=getchar();}
}
const int N=20000005;
const int M=1000000007;
int fac[N],inv[N];
int qpow(int a,int b){int res=1;while(b){if(b&1)res=(1ll*res*a)%M; a=(1ll*a*a)%M; b>>=1;}return res;}
void init(){
fac[0]=fac[1]=1;
for(int i=2;i<=20000000;i++)
fac[i]=(1ll*fac[i-1]*i)%M;
inv[N-5]=qpow(fac[N-5],M-2);
for(int i=N-5;i;i--)inv[i-1]=(1ll*inv[i]*i)%M;
}
int C(int n,int m){return (m>n)?0:1ll*fac[n]*inv[n-m]%M*inv[m]%M;}
int main(){
freopen("tg.in","r",stdin);
freopen("tg.out","w",stdout);
int T,n,x,y; read(T); init();
while(T--){
read(n); read(x); read(y);
if(x>y) swap(x,y);
printf("%lld\n",1ll*(C(x+y-2,y-1)-C(x+y-2,y)+M)%M*(C(n*2-x-y,n-y)-C(n*2-x-y,n-y-1)+M)%M);
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号