机器学习—决策树—分类与回归树(CART)算法

1 CART算法

CART全称叫Classification and Regression Tree，即分类与回归树。CART假设决策树是二叉树，内部结点特征的取值只有“是”和“否”，左分支是取值为“是”的分支，有分支则相反。这样的决策树等价于递归地二分每个特征。 

CART分类回归树可以做分类或者回归。如果待预测结果是离散型数据，则CART生成分类决策树；如果待预测结果是连续型数据，则CART生成回归决策树。数据对象的属性特征为离散型或连续型，并不是区别分类树与回归树的标准。CART作为分类决策树时，待预测样本落至某一叶子节点，则输出该叶子节点中所有样本所属类别最多的那一类（即叶子节点中的样本可能不是属于同一个类别，则多数为主）；作为回归决策树时，待预测样本落至某一叶子节点，则输出该叶子节点中所有样本的均值。

1.1 CART分类树

CART分类树使用基尼指数作为节点划分依据，我们通过例题分析CART分类树实现过程。

1.1.1 例题

下表5-1为拖欠贷款人员训练样本数据集，使用CART算法基于该表数据构造决策树模型，并使用5-2表中测试样本集确定剪枝后的最优子树。

表5-1 拖欠贷款人员训练样本数据集

编号	房产状况	婚姻情况	年收（千元）	拖欠贷款
1	是	单身	125	否
2	否	已婚	100	否
3	否	单身	70	否
4	是	已婚	120	否
5	否	高异	95	是
6	否	已婚	60	否
7	是	高异	220	否
8	否	单身	85	是
9	否	已婚	75	否
10	否	单身	90	是

 

 

表5-2 拖欠贷款人员测试样本数据集

编号	房产状况	婚姻情况	年收入（千元）	拖欠贷款
1	否	已婚	225	否
2	否	已婚	50	是
3	否	单身	89	是
4	是	已婚	320	否
5	是	离异	150	是
6	否	离异	70	否

 

【解】对于房产状况特征，根据是否有房划分数据集：

𝐷(有)={1,4,7}；𝐷(无)={2,3,5,6,8,9,10}

𝐷(有)和𝐷(无)的基尼指数为：

$Gini(D(有))=1-(\frac{3}{3})^2-(\frac{0}{3})^2=0$

$Gini(D(无))=1-(\frac{4}{7})^2-(\frac{3}{7})^2=0.4849$

 房产状况特征对𝐷进行子集划分时所得的基尼指数为：

$Gini(D,房产状态)=\frac{3}{10}\times Gini(D(有))+\frac{7}{10}\times Gini(D(无))=0.343$

对婚姻情况特征划分，因为婚姻状况有三种，需对其构造二元划分：

“婚姻情况=已婚”和“婚姻情况≠已婚”

“婚姻情况=单身”和“婚姻情况≠单身”

“婚姻情况=离异”和“婚姻情况≠离异”

每种取值形式所对应的基尼指数分别为：

$Gini(D,婚姻)=\frac{4}{10}\times Gini(D(已婚))+\frac{6}{10}\times Gini(D(¬已婚))=0.3$

$Gini(D,婚姻)=\frac{4}{10}\times Gini(D(单身))+\frac{6}{10}\times Gini(D(¬单身))=0.3667$

$Gini(D,婚姻)=\frac{2}{10}\times Gini(D(离异))+\frac{8}{10}\times Gini(D(¬离异))=0.4$

(对比上述计算结果，取值分组：

“婚姻情况=已婚”和“婚姻情况≠已婚”

故取：Gini(𝐷,婚姻)=0.3

年收入特征具体做法如下：
首先依据“年收入”特征取值对样本进行升序排序，从小到大依次用“年收入”特征相邻取值的均值作为划分阈值，将训练样本集划分为两个子集。结果如下表所示：

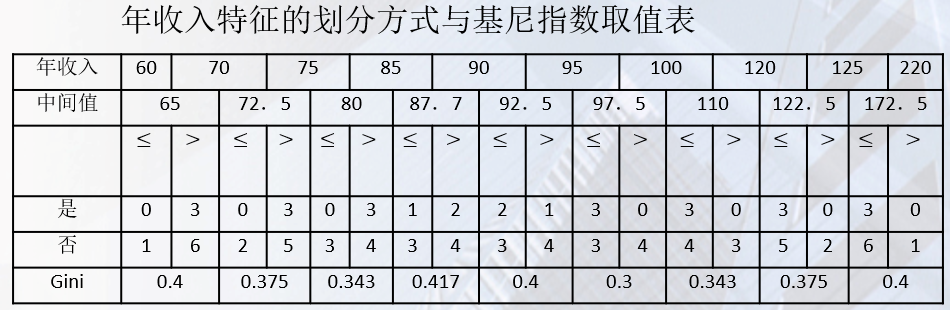
使用年收入特征对𝐷进行划分的最小基尼指数为：

Gini(𝐷,R=97.5)=0.3

 

婚姻情况和年收入特征所对应基尼指数并列最小，均为0.3。
不妨选取婚姻状况作为第一个划分点，将集合𝐷划分为

𝐷(已婚)={2,4,6,9}和𝐷(¬已婚)={1,3,5,7,8,10}

得到如图所示的初始决策树。

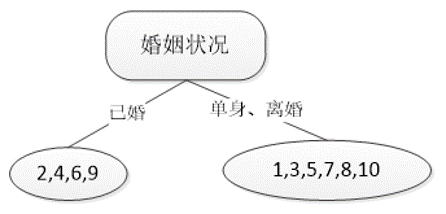
𝐷(已婚)中所有人均不欠贷款，故无需再划分；
𝐷(¬已婚)递归调用上述过程继续划分，最后得到完整决策树，其中𝑌和𝑁分别表示两类不同取值样本数目。

 

1.2 CART回归树

 CART决策树的生成就是递归地构建二叉决策树的过程，对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。

回归决策树（简称回归树）中，采用启发式搜索方法。假设有n个特征，每个特征有S_i个取值，遍历所有特征，尝试该特征所有取值，对空间进行划分，直到取到特征j的取值s，使得损失函数最小，这样就得到1个划分点。公式如下：

$\underset{j,s}{\mathbf{min}}[\underset{C_1}{\mathbf{min}}\textit{{Loss}}(y_i,C_1)+\underset{C_2}{\mathbf{min}}\textit{{Loss}}(y_i,C_2)]$    (1)

假设将输入空间划分为M个单元，R₁,R₂,...，R_m。并在每个单元R_m上有一个固定输出值为$C_m=\mathbf{avg}(y_i|x_i\in R_m)$，C_m也就是该区域内所有点y值的平均数。

1.2.1 算法描述

输入：训练数据集D

输出：回归数f(x)

与线性回归相似，需要1个损失函数对回归效果进行评估，这里采用平方残差和RSS进行评估：

$RSS=\sum_{j=1}^{J}\sum_{i\in R_j}(y_i-\hat{y}_{R_j})^2$       (2)

上式内层$\sum_{}^{}$就是将该区域内所有样本预测值和真实值的差值平方进行求和。外层$\sum_{}^{}$就是遍历所有划分出来的区域。

公式(1)中，先寻找最优C₁、C₂使R₁、R₂的误差平方和最小，数学上很容易证明，当C₁、C₂分别为子集R₁、R₂的y的均值时成立，此时(1)式写成：

$\underset{j,s}{\mathbf{min}}[(\sum_{x_i\in R_1(j,s)}^{}(y_i-\bar{C_1})^2+(\sum_{x_i\in R_2(j,s)}^{}(y_i-\bar{C_2})^2]$     (3)

上式中，使表达式值最小的j(特征)和s(特征下对应的取值)值就是划分依据值。

这样，对于每一个(j,s)，都会根据(3)式得到一个数值，然后取得使(3)式最小的(j,s)，作为最优切分点。

找到最优切分点后，将样本切分为左右两个子节点，子节点的输出值为该节点内所有样本y的均值。

1.2.2 算法流程

在训练数据集所在的输入空间中，递归将每个区域划分为两个子区域，并决定每个子区域上的输出值，构建二叉树。

（1）选择最优切分特征j与切分点要，求解：

 $\underset{j,s}{\mathbf{min}}[\underset{C_1}{\mathbf{min}}\sum_{x_1\in R_{1}(j,s)}^{}(y_i-C_1)^2+\underset{C_2}{\mathbf{min}}\sum_{x_2\in R_{2}(j,s)}^{}(y_i-C_2)^2]$

（2）用选定的对(j,s)划分区域并决定相应的输出值：

 $R_{1(j,s)}=x|x^{(j)}\leqslant s, R_{2(j,s)}=x|x^{(j)}> s$

$\hat{C_m}=\frac{1}{N}\sum_{x_{1}\in R_{m(j,s)}}^{}y_{i},x\in R_{m},m=1,2$

（3）继续对两个区域调用步骤（1）和步骤（2），直到满足停止条件。 

（4）将输入空间划分为M个区域R₁、R₂、...、R_m，生成决策树。

 $f(x)=\sum_{m=1}^{M}\hat{C_{m}}I(x\in R_{m})$

1.2.3 例题

 已知一批样本数据如下表所示，其中x为输入特征对应值，y为输出值，请建立该批数据的CART。

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9	9.05

1.2.4 解析

（1）选择最优切分特征j与最优切分点s：

 确定第一个问题，选择最优特征，本数据据中，只有一个特征，因此，最优切分特征是x。

一共有10组数据，取中位数，得到9个切分点[5.56，5.7，5.91，6.4，6.8，7.05，8.9，8.7，9，9.05]。损失函数定义为最小平方损失函数。

$Loss(y,f(x))=(f(x)-y)^{2}$，将上述9个切分点依次代入下面公式，其中：

$C_{m}=\mathbf{avg}(y_{i}|x_{i}\in R_{m})$

a)计算子区域输出值：

例如，取s=1.5，此时区域1为R1=1，区域2为R2=2，3，4，5，6，7，8，9，10，这两个区域输出值分别为：

C1=5.56

C2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.50

同理，取分别取s为2.5-9.5，计算结果如下：

S	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
C1	5.56	5.63	5.72	5.89	6.07	6.24	3.62	6.88	7.11
C2	7.5	7.73	7.99	8.25	8.54	8.91	8.92	9.03	9.05

b)计算损失函数值，找到最优切分点：把C1、C2的值代入到平方损失函数$Loss(y,f(x))=(f(x)-y)^{2}$：

当s=1.5时，

L(1.5)=(5.56-5.56)²+[(5.7-7.5)²+(5.91-7.5)²+...+(9.05-7.5)²]=15.72，同理得：

S	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
m(s)	15.72	12.07	8.36	5.78	3.91	1.93	8.01	11.73	15.74

显然，当s=6.5时，m(s)最小，因此第一个划分变量为(j=x,s=6.5)。

（2）用选定的(j,s)划分区域并决定输出值：

 两个区域是R1={1,2,3,4,5,6}，R2={7,8,9,10}

输出值$C_{m}=\mathbf{avg}(y_{i}|x_{i}\in R_{m})$，C1=6.24，C2=8.91

（3）调用步骤（1）、（2），继续划分：

 

x	1	2	3	4	5	6
y	5.56	5.7	5.91	6.4	6.8	7.05

取划分点[1.5,2.5,3.5,4.5,5.5]，则各区域输出值c如下表：

S	1.5	2.5	3.5	4.5	5.5
C1	5.56	5.63	5.72	5.89	6.07
C2	6.37	6.54	6.75	6.93	7.05

计算损失函数值m(s)

S	1.5	2.5	3.5	4.5	5.5
m(s)	1.3087	0.754	0.2771	0.4368	1.0644

当s=3.5时，m(s)值最小。

（4）生成回归树，假设在生成3个区域后停止划分，则生成的回归树形式如下：

 $T=\left\{\begin{matrix}5.72 & x\leqslant 3.5 \\6.75 & 3.5<x\leqslant 6.5 \\8.91 & 6.5<x \\\end{matrix}\right.$