openGauss源码解析（105）

openGauss源码解析：SQL引擎源解析（20）

3. 选择算子

在种群生成之后，就可以进行代际遗传优化，从种群中随机选择两个染色做交叉操作，这样就能产生一个新的染色体。

由于种群中的染色体已经按照适应度排序了，对来说适应度越低（代价越低）的染色体越好，因为希望将更好的染色体遗传下去，所以需要在选择父染色体和母染色体的时候更倾向于选择适应度低的染色体。在选择过程中会涉及倾向（bias）的概念，它在算子中是一个固定的值。当然，bias的值可以通过参数Geqo_selection_bias进行调整（默认值为2.0）。

/* 父染色体和母染色体通过linear_rand函数选择 */

first = linear_rand(root, pool->size, bias);

second = linear_rand(root, pool->size, bias);

要生成基于某种概率分布的随机数（），需要首先知道概率分布函数或概率密度函数，openGauss数据库采用的概率密度函数（probability density function，PDF）为：

通过概率密度函数获得累计分布函数（cumulative distribution function，CDF）：

然后通过概率分布函数根据逆函数法可以获得符合概率分布的随机数。

对于函数。

求逆函数。

这和源代码中linear_rand函数的实现是一致的。

/* 先求的值 */

double sqrtval;

sqrtval = (bias * bias) - 4.0 * (bias - 1.0) * geqo_rand(root);

if (sqrtval > 0.0)

sqrtval = sqrt(sqrtval);

/* 然后计算的值，其为基于概率分布随机数且符合[0,1]分布 */

/* max是种群中染色体的数量 */

/* index就是满足概率分布的随机数，且随机数的值域在[0, max] */

index = max * (bias - sqrtval) / 2.0 / (bias - 1.0);

把基于概率的随机数生成算法的代码提取出来单独进行计算验证，看一下它生成随机数的特点。设bias = 2.0，然后利用概率密度函数计算各个区间的理论概率值进行分析，比如对于0.6~0.7的区间，计算其理论概率如下。

各个区间的理论概率值如图6-15所示。

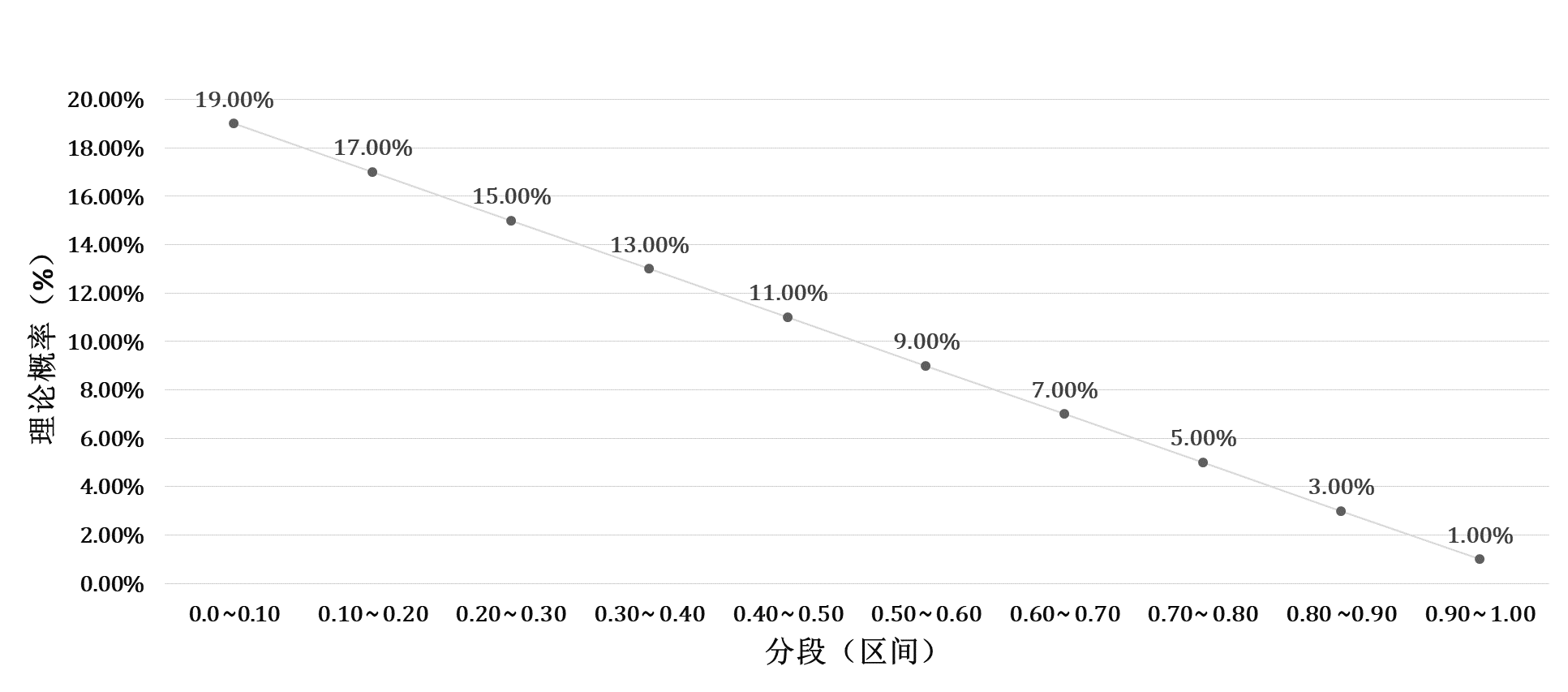
图6-15 随机数生成理论概率值

从图6-15可以看出各个区间的理论概率值的数值是依次下降的，也就是说在选择父母染色体的时候是更倾向于选择适应度更低（代价更低）的染色体。