openGauss源码解析（97）

openGauss源码解析：SQL引擎源解析（12）

6.3.4 动态规划

目前openGauss已经完成了基于规则的查询重写优化和逻辑分解优化，并且已经生成各个基表的物理路径。基表的物理路径仅仅是优化器规划中很小的一部分，现在openGauss将进入优化器优化的另一个重要的工作，即生成Join连接路径。openGauss采用的是自底向上的优化方式，对于多表连接路径主要采用的是动态规划和遗传算法两种方式。这里主要介绍动态规划的方式，但如果表数量有很多，就需要用遗传算法。遗传算法可以避免在表数量过多情况下带来的连接路径搜索空间膨胀的问题。对于一般场景采用动态规划的方式即可，这也是openGauss默认采用的优化方式。

经过逻辑分解优化后，语句中的表已经被拉平，即从原来的树状结构变成了扁平的数组结构。各个表之间的连接关系也被记录到了root目录下的SpecialJoinInfo结构体中，这些也是对连接做动态规划的基础。

1. 动态规划方法

首先动态规划方法适用于包含大量重复子问题的最优解问题，通过记忆每个子问题的最优解，使相同的子问题只求解一下，下次就可以重复利用上次子问题求解的记录即可，这就要求这些子问题的最优解能够构成整个问题的最优解，也就是说应该要具有最优子结构的性质。所以对于语句的连接优化来说，整个语句连接的最优解也就是某一块语句连接的最优解，在规划的过程中无法重复计算局部最优解，直接用上次计算的局部最优解即可。

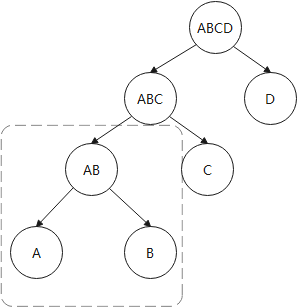
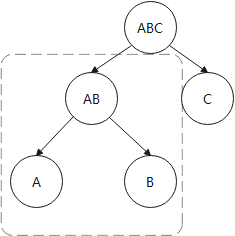
图6-9 重复子问题的最优解

例如，图6-9中两个连接树中A×B的连接操作就属于重复子问题，因为无论是生成A×B×C×D还是A×B×C连接路径的时候都需要先生成A×B连接路径，对于多表连接生成的路径即很多层堆积的情况下可能有上百种连接的方法，这些连接树的重复子问题数量会比较多，因此连接树具有重复子问题，可以一次求解多次使用，也就是对于连接A×B只需要一次生成最优解即可。

多表连接动态规划算法代码主要是从make_rel_from_joinlist函数开始的，如图6-10所示。

图6-10 多表连接动态规划算法

1） make_rel_from_joinlist函数

动态规划的实现代码主入口是从make_rel_from_joinlist函数开始的，它的输入参数是deconstruct_jointree函数拉平之后的RangeTableRef链表，每个RangeTableRef代表一个表，然后就可以根据这个链表来查找基表的RelOptInfo结构体，用查找到的RelOptInfo去构建动态规划连接算法一层中的基表RelOptInfo，后续再继续在这第1层RelOotInfo进行“累积”。代码如下：

//遍历拉平之后的joinlist，这个链表是RangeTableRef的链表

foreach(jl, joinlist)

{

Node *jlnode = (Node *) lfirst(jl);

RelOptInfo *thisrel;

//多数情况下都是RangeTableRef链表，根据RangeTableRef链表中存放的下标值（rtindex）

//查找对应的RelOptInfo

if (IsA(jlnode, RangeTblRef))

{

int varno = ((RangeTblRef *) jlnode)->rtindex;

thisrel = find_base_rel(root, varno);

}

//受到from_collapse_limit参数和join_collapse_limit参数的影响，也存在没有拉平的节点，这里递归调用make_rel_from_joinlist函数

else if (IsA(jlnode, List))

thisrel = make_rel_from_joinlist(root, (List *) jlnode);

else

ereport (……);

//这里就生成了第一个初始链表，也就是基表的链表，这个链表是

//动态规划方法的基础

initial_rels = lappend(initial_rels, thisrel);

}

2） standard_join_search函数

动态规划方法在累积表的过程中，每一层都会增加一个表，当所有的表都增加完毕的时候，最后的连接树也就生成了。因此累积的层数也就是表的数量，如果存在N个表，那么在此就要堆积N次，具体每一层堆积的过程在函数join_search_one_level中进行介绍，那么这个函数中主要做的还是为累积连接进行准备工作，包括分配每一层RelOptInfo所占用的内存空间以及每累积一层RelOptInfo后保留部分信息等工作。

创建一个“连接的数组”，类似于[LIST1, LIST2, LIST3]的结构，其中数组中的链表就用来保存动态规划方法中一层所有的RelOptInfo，例如数组中的第一个链表存放的就是有关所有基表路径的链表。代码如下：

//分配“累积”过程中所有层的RelOptInfo链表

root->join_rel_level = (List**)palloc0((levels_needed + 1) * sizeof(List*));

//初始化第1层所有基表RelOptInfo

root->join_rel_level[1] = initial_rels;

做好了初始化工作之后，就可以开始尝试构建每一层的RelOptInfo。代码如下：

for (lev = 2; lev <= levels_needed; lev++) {

ListCell* lc = NULL;

//在join_search_one_level函数中生成对应的lev层的所有RelOptInfo

join_search_one_level(root, lev);

……

}

3） join_search_one_level函数

join_search_one_level函数主要用于生成一层中的所有RelOptInfo，如图6-11所示。如果要生成第N层的RelOptInfo主要有三种方式：一是尝试生成左深树和右深树，二是尝试生成浓密树，三是尝试生成笛卡儿积的连接路径（俗称遍历尝试）。

图6-11 生成第N层的RelOptInfo方式

（1） 左深树和右深树。

左深树和右深树生成的原理是一样的，只是在make_join_rel函数中对候选出的待连接的两个RelOptInfo进行位置互换，也就是每个RelOptInfo都有一次作为内表或作为外表的机会，这样其实创造出更多种连接的可能有助于生成最优路径。

如图6-12所示两个待选的RelOptInfo要进行连接生成A×B×C，左深树也就是对A×B和C进行了一下位置互换，A×B作为内表形成了左深树，A×B作为外表形成了右深树。

图6-12 左深树和右深树示意图

具体代码如下：

//对当前层的上一层进行遍历，也就是说如果要生成第4层的RelOptInfo

//就要取第3层的RelOptInfo和第1层的基表尝试做连接

foreach(r, joinrels[level - 1])

{

RelOptInfo *old_rel = (RelOptInfo *) lfirst(r);

//如果两个RelOptInfo之间有连接关系或者连接顺序的限制

//优先给这两个RelOptInfo生成连接

// has_join_restriction函数可能误判，不过后续还会有更精细的筛查

if (old_rel->joininfo != NIL || old_rel->has_eclass_joins ||

has_join_restriction(root, old_rel))

{

ListCell *other_rels;

//要生成第N层的RelOptInfo，就需要第N-1层的RelOptInfo和1层的基表集合进行连接

//即如果要生成第2层的RelOptInfo，那么就变成第1层的RelOptInfo和第1层的基表集合进行连接

//因此，需要在生成第2层基表集合的时候做一下处理，防止自己和自己连接的情况

if (level == 2)

other_rels = lnext(r);

else

other_rels = list_head(joinrels[1]);

//old_rel“可能”和其他表有连接约束条件或者连接顺序限制

//other_rels中就是那些“可能”的表，make_rels_clause_joins函数会进行精确的判断

make_rels_by_clause_joins(root, old_rel, other_rels);

}

else

{

//对没有连接关系的表或连接顺序限制的表也需要尝试生成连接路径

make_rels_by_clauseless_joins(root, old_rel, list_head(joinrels[1]));

}

}

（2） 浓密树。

要生成第N层的RelOptInfo，左深树或者右深树是将N-1层的RelOptInfo和第1层的基表进行连接，不论是左深树，还是右深树本质上都是通过引用基表RelOptInfo去构筑当前层RelOptInfo。而生成浓密树抛开了基表，它是将各个层次的RelOptInfo尝试进行随意连接，例如将第N-2层RelOptInfo和第2层的RelOptInfo进行连接，依次可以类推出（2，N﹣2）、(3，N﹣3)、(4, N﹣4)等多种情况。浓密树的建立要满足两个条件：一是两个RelOptInfo要存在相关的约束条件或者存在连接顺序的限制，二是两个RelOptInfo中不能存在有交集的表。

for (k = 2;; k++)

{

int other_level = level - k;

foreach(r, joinrels[k])

{

//有连接条件或者连接顺序的限制

if (old_rel->joininfo == NIL && !old_rel->has_eclass_joins &&

!has_join_restriction(root, old_rel))

continue;

……

for_each_cell(r2, other_rels)

{

RelOptInfo *new_rel = (RelOptInfo *) lfirst(r2);

//不能有交集

if (!bms_overlap(old_rel->relids, new_rel->relids))

{

//有相关的连接条件或者有连接顺序的限制

if (have_relevant_joinclause(root, old_rel, new_rel) ||

have_join_order_restriction(root, old_rel, new_rel))

{

(void) make_join_rel(root, old_rel, new_rel);

}

}

}

}

}

（3） 笛卡儿积。

在尝试过左深树、右深树以及浓密树之后，如果还没有生成合法连接，那么就需要努力对第N﹣1层和第1层的RelOptInfo做最后的尝试，其实也就是将第N﹣1层中每一个RelOptInfo和第1层的RelOptInfo合法连接的尝试。