openGauss源码解析（92）

openGauss源码解析：SQL引擎源解析（7）

6.3 查询优化

openGauss数据库的查询优化过程功能比较明晰，从源代码组织的角度来看，相关代码分布在不同的目录下，如表6-6所示。

表6-6 查询优化模块说明

模块	目录	说明
查询重写	src/gausskernel/optimizer/prep	主要包括子查询优化、谓词化简及正则化、谓词传递闭包等查询重写优化技术
统计信息	src/gausskernel/optimizer/commands/analyze.cpp	生成各种类型的统计信息，供选择率估算、行数估算、代价估算使用
代价估算	src/common/backend/utils/adt/selfuncs.cpp src/gausskernel/optimizer/path/costsize.cpp	进行选择率估算、行数估算、代价估算
物理路径	src/gausskernel/optimizer/path	生成物理路径
动态规划	src/gausskernel/optimizer/plan	通过动态规划方法对物理路径进行搜索
遗传算法	src/gausskernel/optimizer/geqo	通过遗传算法对物理路径进行搜索

6.3.1 查询重写

SQL语言是丰富多样的，非常的灵活，不同的开发人员依据经验的不同，手写的SQL语句也是各式各样，另外还可以通过工具自动生成。SQL语言是一种描述性语言，数据库的使用者只是描述了想要的结果，而不关心数据的具体获取方式，输入数据库的SQL语言很难做到是以最优形式表示的，往往隐含了一些冗余信息，这些信息可以被挖掘用来生成更加高效的SQL语句。查询重写就是把用户输入的SQL语句转换为更高效的等价SQL，查询重写遵循两个基本原则。

（1） 等价性：原语句和重写后的语句，输出结果相同。

（2） 高效性：重写后的语句，比原语句在执行时间和资源使用上更高效。

查询重写主要是基于关系代数式的等价变换，关系代数的变换通常满足交换律、结合律、分配率、串接率等，如表6-7所示。

表6-7 关系代数等价变换

等价变换	内容
交换律	A × B == B × A A ⨝B == B ⨝ A A ⨝F B == B ⨝F A ……其中F是连接条件 Π p(σF (B)) == σF (Π p(B)) ……其中F∈p
结合律	(A × B) × C==A × (B × C) (A ⨝ B) ⨝ C==A ⨝ (B ⨝ C) (A ⨝F1 B) ⨝F2 C==A ⨝F1 (B ⨝F2 C) …… F1和F2是连接条件
分配律	σF(A × B) == σF(A) × B …… 其中F ∈ A σF(A × B) == σF1(A) × σF2(B) …… 其中F = F1 ∪ F2，F1∈A, F2 ∈B σF(A × B) == σFX (σF1(A) × σF2(B)) …… 其中F = F1∪F2∪FX，F1∈A, F2 ∈B Π p,q(A × B) == Π p(A) × Π q(B) …… 其中p∈A，q∈B σF(A × B) == σF1(A) × σF2(B) …… 其中F = F1 ∪ F2，F1∈A, F2 ∈B σF(A × B) == σFx (σF1(A) × σF2(B)) …… 其中F = F1∪F2∪Fx，F1∈A, F2 ∈B
串接律	Π P=p1,p2,…pn(Π Q=q1,q2,…qn(A)) == Π P=p1,p2,…pn(A)……其中P ⊆ Q σF1(σF2(A)) == σF1∧F2(A)

查询重写优化既可以基于关系代数的理论进行优化，例如谓词下推、子查询优化等，也可以基于启发式规则进行优化，例如Outer Join消除、表连接消除等。另外还有一些基于特定的优化规则和实际执行过程相关的优化，例如在并行扫描的基础上，可以考虑对Aggregation算子分阶段进行，通过将Aggregation划分成不同的阶段，可以提升执行的效率。

从另一个角度来看，查询重写是基于优化规则的等价变换，属于逻辑优化，也可以称为基于规则的优化，那么怎么衡量对一个SQL语句进行查询重写之后，它的性能一定是提升的呢？这时基于代价对查询重写进行评估就非常重要了，因此查询重写不只是基于经验的查询重写，还可以是基于代价的查询重写。

以谓词传递闭包和谓词下推为例，谓词的下推能够极大的降低上层算子的计算量，从而达到优化的效果，如果谓词条件有存在等值操作，那么还可以借助等值操作的特性来实现等价推理，从而获得新的选择条件。

例如，假设有两个表t1、t2分别包含[1,2,3,..100]共100行数据，那么查询语句SELECT t1.c1, t2.c1 FROM t1 JOIN t2 ON t1.c1=t2.c1 WHERE t1.c1=1则可以通过选择下推和等价推理进行优化，如图6-6所示。

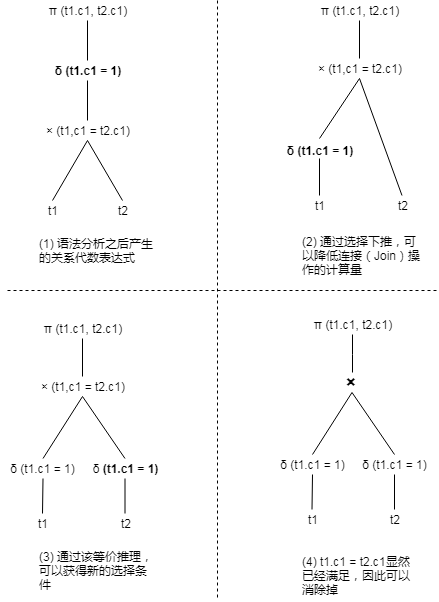
图6-6 查询重写前后对比图

如图6-6-（1）所示，t1、t2表都需要全表扫描100行数据，然后再做join，生成100行数据的中间结果，最后再做选择操作，最终结果只有1行数据。如果利用等价推理，可以得到{t1.c1, t2.c1, 1}的是互相等价的，从而推导出新的t2.c1=1的选择条件，并把这个条件下推到t2上，从而得到图6-6-（4）重写之后的逻辑计划。可以看到，重写之后的逻辑计划，只需要从基表上面获取1条数据即可，join时内、外表的数据也只有1条，同时省去了在最终结果上的过滤条件，性能大幅提升。

在代码层面，查询重写的架构大致如图6-7所示。

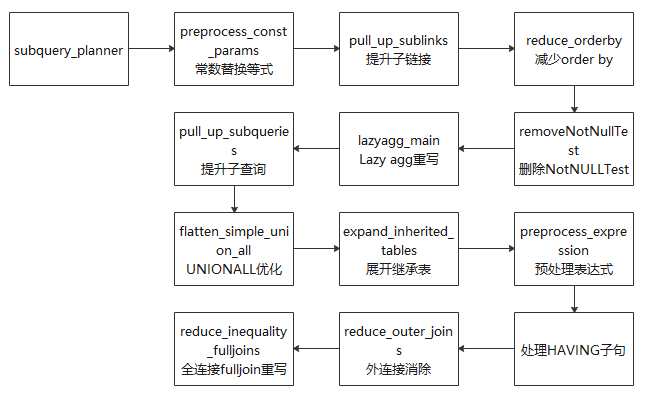
图6-7 查询重写的架构

（1） 提升子查询：子查询出现在RangeTableEntry中，它存储的是一个子查询树，若子查询不被提升，则经过查询优化之后形成一个子执行计划，上层执行计划和子查询计划做嵌套循环得到最终结果。在该过程中，查询优化模块对这个子查询所能做的优化选择较少。若该子查询被提升，转换成与上层的join，由查询优化模块常数替换等式：由于常数引用速度更快，故将可以求值的变量求出来，并用求得的常数替换它，实现函数为preprocess_const_params。

（2） 子查询替换CTE：理论上CTE（common table expression，通用表达式）与子查询性能相同，但对子查询可以进行进一步的提升重写优化，故尝试用子查询替换CTE，实现函数为substitute_ctes_with_subqueries。

（3） multi count(distinct)替换为多条子查询：如果出现该类查询，则将多个count(distinct)查询分别替换为多条子查询，其中每条子查询中包含一个count(distinct)表达式，实现函数为convert_multi_count_distinct。

（4） 提升子链接：子链接出现在WHERE/ON等约束条件中，通常伴随着ANY/ALL/IN/EXISTS/SOME等谓词同时出现。虽然子链接从语句的逻辑层次上是清晰的，但是效率有高有低，比如相关子链接，其执行结果和父查询相关，即父查询的每一条元组都对应着子链接的重新求值，此情况下可通过提升子链接提高效率。在该部分数据库主要针对ANY和EXISTS两种类型的子链接尝试进行提升，提升为Semi Join或者Anti-SemiJoin，实现函数为pull_up_sublinks。

（5） 减少ORDER BY：由于在父查询中可能需要对数据库的记录进行重新排序，故减少子查询中的ORDER BY语句以进行链接可提高效率，实现函数为reduce_orderby。

（6） 删除NotNullTest：即删除相关的非NULL Test以提高效率，实现函数为removeNotNullTest。

（7） Lazy Agg重写：顾名思义，即“懒聚集”，目的在于减少聚集次数，实现函数为lazyagg_main。

（8） 对连接操作的优化做了很多工作，可能获得更好的执行计划，实现函数为pull_up_subqueries。

（9） UNION ALL优化：对顶层的UNION ALL进行处理，目的是将UNION ALL这种集合操作的形式转换为AppendRelInfo的形式，实现函数为flatten_simple_union_all。

（10） 展开继承表：如果在查询语句执行的过程中使用了继承表，那么继承表是以父表的形式存在的，需要将父表展开成为多个继承表，实现函数为expand_inherited_tables。，实现函数为expand_inherited_tables。

（11）预处理表达式：该模块是对查询树中的表达式进行规范整理的过程，包括对链接产生的别名Var进行替换、对常量表达式求值、对约束条件进行拉平、为子链接生成执行计划等，实现函数为preprocess_expression。

（12） 处理HAVING子句：在Having子句中，有些约束条件是可以转变为过滤条件的（对应WHERE），这里对Having子句中的约束条件进行拆分，以提高效率。

（13） 外连接消除：目的在于将外连接转换为内连接，以简化查询优化过程，实现函数为reduce_outer_join函数。

（14） 全连接full join重写：对全连接函数进行重写，以完善其功能。比如对于语句SELECT * FROM t1 FULL JOIN t2 ON TRUE可以将其转换为： SELECT * FROM t1 LEFT JOIN t2 ON TRUE UNION ALL (SELECT * FROM t1 RIGHT ANTI FULL JOIN t2 ON TRUE)，实现函数为reduce_inequality_fulljoins。

下面以子链接提升为例，介绍openGauss中一种最重要的子查询优化。所谓子链接（SubLink）是子查询的一种特殊情况，由于子链接出现在WHERE/ON等约束条件中，因此经常伴随ANY/EXISTS/ALL/IN/SOME等谓词出现，openGauss数据库为不同的谓词设置了不同的SUBLINK类型。代码如下：

Typedef enum SubLinkType {

EXISTS_SUBLINK,

ALL_SUBLINK,

ANY_SUBLINK,

ROWCOMPARE_SUBLINK,

EXPR_SUBLINK,

ARRAY_SUBLINK,

CTE_SUBLINK

} SubLinkType;

openGauss数据库为子链接定义了单独的结构体——SubLink结构体，其中主要描述了子链接的类型、子链接的操作符等信息。代码如下：

Typedef struct SubLink {

Expr xpr;

SubLinkType subLinkType;

Node* testexpr;

List* operName;

Node* subselect;

Int location;

} SubLink;

子链接提升相关接口函数如图6-8所示。

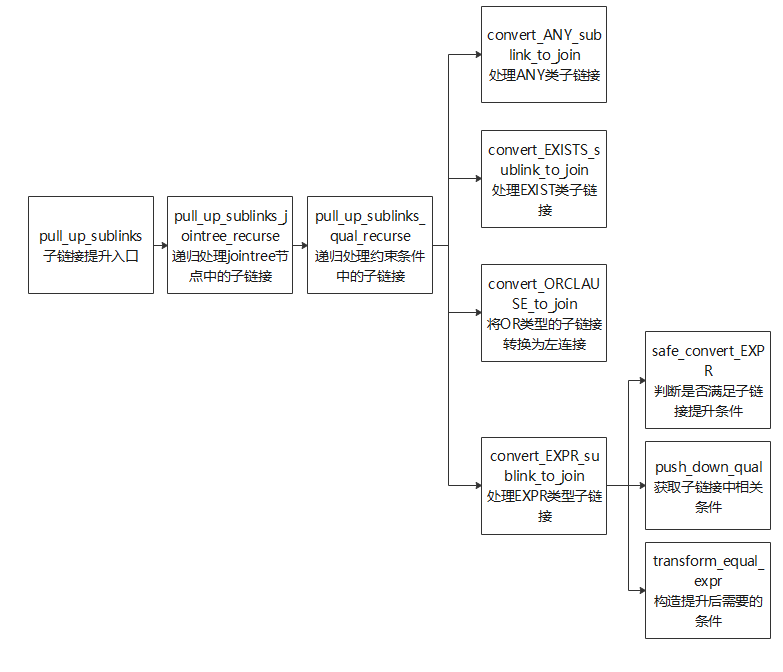
图6-8 子链接相关接口函数

子链接提升的主要过程是在pull_up_sublinks函数中实现，pull_up_sublinks函数又调用pull_up_sublinks_jointree_recurse递归处理Query->jointree中的节点，函数输入参数如表6-8所示。

表6-8 函数输入参数说明

参数名	参数类型	说明
root	PlannerInfo*	输入参数，查询优化模块的上下文信息
jnode	Node*	输入参数，需要递归处理的节点，可能是RangeTblRef、FromExpr或JoinExpr
relids	Relids*	输出参数，jnode参数中涉及的表的集合
返回值	Node*	经过子链接提升处理之后的node节点

jnode分为三种类型：RangeTblRef、FromExpr、JoinExpr。针对这三种类型pull_up_sublinks_jointree_recurse函数分别进行了处理。

1） RangeTblRef

RangeTblRef是Query->jointree的叶子节点，所以是该函数递归结束的条件，程序走到该分支，一般有两种情况。

（1） 当前语句是单表查询而且不存在连接操作，这种情况递归处理直到结束后，再去查看子链接是否满足其他提升条件。

（2） 查询语句存在连接关系，在对From->fromlist、JoinExpr->larg或者JoinExpr->rarg递归处理的过程中，当遍历到了RangeTblRef叶子节点时，需要把RangeTblRef节点的relids（表的集合）返回给上一层。主要用于判断该子链接是否能提升。

2） FromExpr

（1） 递归遍历From->fromlist中的节点，之后对每个节点递归调用pull_up_sublinks_jointree_recurse函数，直到处理到叶子节点RangeTblRef才结束。

（2） 调用pull_up_sublinks_qual_recurse函数处理From->qual，对其中可能出现的ANY_SUBLINK或EXISTS_SUBLINK进行处理。

3） JoinExpr

（1） 调用pull_up_sublinks_jointree_recurse函数递归处理JoinExpr->larg和JoinExpr->rarg，直到处理到叶子节点RangeTblRef才结束。另外还需要根据连接操作的类型区分子链接是否能够被提升。

（2） 调用pull_up_sublinks_qual_recurse函数处理JoinExpr->quals，对其中可能出现的ANY_SUBLINK或EXISTS_SUBLINK做处理。如果连接类型不同，pull_up_sublinks_qual_recurse函数的available_rels1参数的输入值是不同的。

pull_up_sublinks_qual_recurse函数除了对ANY_SUBLINK和EXISTS_SUBLINK做处理，还对OR子句和EXPR类型子链接做了查询重写优化。其中Expr类型的子链接提升代码逻辑如下。

（1） 通过safe_convert_EXPR函数判断sublink是否可以提升。代码如下：

//判断当前SQL语句是否满足sublink提升条件

if (subQuery->cteList ||

subQuery->hasWindowFuncs ||

subQuery->hasModifyingCTE ||

subQuery->havingQual ||

subQuery->groupingSets ||

subQuery->groupClause ||

subQuery->limitOffset ||

subQuery->rowMarks ||

subQuery->distinctClause ||

subQuery->windowClause) {

ereport(DEBUG2,

(errmodule(MOD_OPT_REWRITE),

(errmsg("[Expr sublink pull up failure reason]: Subquery includes cte, windowFun, havingQual, group, "

"limitoffset, distinct or rowMark."))));

return false;

}

（2） 通过push_down_qual函数提取子链接中相关条件。代码如下：

Static Node* push_down_qual(PlannerInfo* root, Node* all_quals, List* pullUpEqualExpr)

{

If (all_quals== NULL) {

Return NULL;

}

List* pullUpExprList = (List*)copyObject(pullUpEqualExpr);

Node* all_quals_list = (Node*)copyObject(all_quals);

set_varno_attno(root->parse, (Node*)pullUpExprList, true);

set_varno_attno(root->parse, (Node*)all_quals_list, false);

Relids varnos = pull_varnos((Node*)pullUpExprList, 1);

push_qual_context qual_list;

SubLink* any_sublink = NULL;

Node* push_quals = NULL;

Int attnum = 0;

While ((attnum = bms_first_member(varnos)) >= 0) {

RangeTblEntry* r_table = (RangeTblEntry*)rt_fetch(attnum, root->parse->rtable);

//这张表必须是基表，否则不能处理

If (r_table->rtekind == RTE_RELATION) {

qual_list.varno = attnum;

qual_list.qual_list = NIL;

//获得包含特殊varno的条件

get_varnode_qual(all_quals_list, &qual_list);

If (qual_list.qual_list != NIL && !contain_volatile_functions((Node*)qual_list.qual_list)) {

any_sublink = build_any_sublink(root, qual_list.qual_list, attnum,pullUpExprList);

push_quals = make_and_qual(push_quals, (Node*)any_sublink);

}

list_free_ext(qual_list.qual_list);

}

}

list_free_deep(pullUpExprList);

pfree_ext(all_quals_list);

return push_quals;

}

（3） 通过transform_equal_expr函数构造需要提升的SubQuery（增加GROUP BY子句，删除相关条件）。代码如下：

//为SubQuery增加GROUP BY和windowClasues

if (isLimit) {

append_target_and_windowClause(root,subQuery,(Node*)copyObject(node), false);

} else {

append_target_and_group(root, subQuery, (Node*)copyObject(node));

}

//删除相关条件

subQuery->jointree = (FromExpr*)replace_node_clause((Node*)subQuery->jointree,

(Node*)pullUpEqualExpr,

(Node*)constList,

RNC_RECURSE_AGGREF | RNC_COPY_NON_LEAF_NODES);

（4） 构造需要提升的条件。代码如下：

//构造需要提升的条件

joinQual = make_and_qual((Node*)joinQual, (Node*)pullUpExpr);

…

Return joinQual;

（5） 生成join表达式。代码如下：

//生成join表达式

if (IsA(*currJoinLink, JoinExpr)) {

((JoinExpr*)*currJoinLink)->quals = replace_node_clause(((JoinExpr*)*currJoinLink)->quals,

tmpExprQual,

makeBoolConst(true, false),

RNC_RECURSE_AGGREF | RNC_COPY_NON_LEAF_NODES);

} else if (IsA(*currJoinLink, FromExpr)) {

((FromExpr*)*currJoinLink)->quals = replace_node_clause(((FromExpr*)*currJoinLink)->quals,

tmpExprQual,

makeBoolConst(true, false),

RNC_RECURSE_AGGREF | RNC_COPY_NON_LEAF_NODES);

}

rtr = (RangeTblRef *) makeNode(RangeTblRef);

rtr->rtindex = list_length(root->parse->rtable);

// 构造左连接的JoinExpr

JoinExpr *result = NULL;

result = (JoinExpr *) makeNode(JoinExpr);

result->jointype = JOIN_LEFT;

result->quals = joinQual;

result->larg = *currJoinLink;

result->rarg = (Node *) rtr;

// 在rangetableentry中添加JoinExpr。在后续处理中，左外连接可转换为内连接

rte = addRangeTableEntryForJoin(NULL,

NIL,

result->jointype,

NIL,

result->alias,

true);

root->parse->rtable = lappend(root->parse->rtable, r