Logistic 最大熵 朴素贝叶斯 HMM MEMM CRF 几个模型的总结
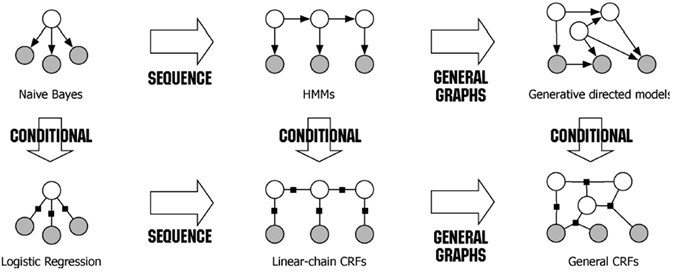
朴素贝叶斯(NB) , 最大熵(MaxEnt) (逻辑回归, LR), 因马尔科夫模型(HMM), 最大熵马尔科夫模型(MEMM), 条件随机场(CRF) 这几个模型之间有千丝万缕的联系，本文首先会证明 Logistic 与 MaxEnt 的等价性，接下来将从图模型的角度阐述几个模型之间的关系，首先用一张图总结一下几个模型的关系：
Logistic（Softmax） MaxEnt 等价性证明
Logistic 是 Softmax 的特殊形式，多以如果 Softmax 与 MaxEnt 是等价的，则 Logistic 与 MaxEnt 是等价的。Softmax 可以理解为多项分布的指数簇分布，指数簇分布都是具有最大熵性质的，其最大熵形式为指数簇分布的似然形式。
给定训练数据 $\left\{(x^{(i)},y^{(i)}\right\}_{i=1}^m$ ，这里 $x^{(i)} \in \mathbb{R}^N$， $y^{(i)} \in \mathbb{R}$ 且 $y^{(i)}$ 的取值是 1,…,K 代表类别，来看一下熟悉的 Softmax 模型:
\[h_k(x) = \frac{e^{w_k^Tx}}{\sum_je^{w_j^Tx}}\]
这里 $h_k(x)$ 代表 x 属于类别 k 的概率，并且有 $\sum_k h_k(x) = 1$ ，训练数据的 $\log$ 似然函数形式如下：
\[L(w) = \sum_i \log h_{y^{(i)}}(x^{(i)})\]
对于 $k = 1,2,…,K$， 对似然函数求导，并另导数得 0 可得：
\begin{aligned}
\frac{\partial L(w)}{\partial w_k} &= 0 \\
\Rightarrow \\
\frac{\partial}{\partial w_k}\sum_i \log h_{y^{(i)}}(x^{(i)}) &= \sum_i \left \{ y^{(i)} - h_k(x^{(i)}) \right \}x^{(i)} \\
&= \sum_i 1(y^{(i)} = k)\cdot x^{(i)} - \sum_i h_k(x^{(i)}) \cdot x^{(i)} = 0
\end{aligned}
关于以上这个推倒，参考文献$^4$ ，这里我们用一个特征函数来代替 $1(y^{(i)} = k)$ ,特征函数的形式如下：
\[f(\mu,v) = \left \{\begin{aligned}
1, \ &if \ \mu = v \\
0, \ &else
\end{aligned}\right .\]
因此得到了 Softmax 的一个重要结论：
\[ \sum_i f(y^{(i)} ,k)\cdot x^{(i)} = \sum_i h_k(x^{(i)}) \cdot x^{(i)} , \ k = 1,2…,K \tag{1}\]
同时要满足：
\[\sum_k h_k(x) = 1 \tag{2}\]
以上的条件 (1) (2) 即可理解为两个约束条件，现在假设对映射函数 $h_k(x)$ 一无所知，我们来用前边两个约束去求解一个 MaxEnt 模型 $h_k(x)$ ,模型的熵为：
\[ – \sum_k \sum_i h_k(x^{(i)}) \log h_k(x^{(i)})\]
根据 MaxEnt 模型的求解形式，列出拉格朗日乘子法公式：
\begin{aligned}
L(w) =- \sum_k \sum_i h_k(x^{(i)}) \log h_k(x^{(i)})+ \sum_k w_k\left \{ \sum_i \left [ h_k(x^{(i)})x^{(i)} - f(y^{(i)},k)x^{(i)}\right ] \right \} + \sum_k\sum_ia_i\left \{ h_k(x^{(i)})-1 \right \}
\end{aligned}
对于任意 $k ,i$，对 $f_k(x^{(i)})$ 求偏导 ：
\[\frac{\partial L(w)}{\partial h_k(x^{(i)}) } = w_k x^{(i)} + a_i –\log h_k(x^{(i)}) – 1 = 0\]
另偏导得 0：
\[h_k(x^{(i)}) = e^{w_k + x^{(i)} +a_i -1 } \tag{*}\]
因此可得：
\[ \sum_j h_j(x^{(i)}) = 1 \Rightarrow e^a = \frac{1}{\sum_j e^{w_j x^{(i)} -1} }\]
带入 (*) 式可得：
\[h_k(x^{(i)}) = \frac{e^{w_k \cdot x}}{\sum_j e^{w_j \cdot x}}\]
这便是 MaxEnt 推倒出 Softmax 的过程，思路就是首先对 Softmax 损失函数求导，然后另导数得 0 ，得到 Softmax 模型需要满足的约束，然后在满足约束的情况下求解 MaxEnt 模型即可，得到的正是 Softmax 模型，所以两者等价的。
接下来直接从 MaxEnt 模型与 Softmax 模型的形式来找出两者的关系，为了描述更加清晰，这里的符号都带有了向量标记，首先来看 Softmax 模型：
\[f_k(\overrightarrow{x}) = \frac{e^{\overrightarrow{w}_k \cdot \overrightarrow{x} }}{\sum_j e^{\overrightarrow{w}_j \cdot \overrightarrow{x} }}\]
在 Softmax 的视角下，每条输入数据会被表示成一个 n 维向量，可以看成 n 个特征。而模型中每一类都有 n 个权重，与 n 个特征相乘后求和再经过 Softmax 的结果，代表这条输入数据被分到这一类的概率。
在MaxEnt 的视角下，每条输入的 n 个“特征”与 k 个类别共同组成了$n \times k$ 个特征，模型中有 $n \times k$ 个权重，与特征一一对应。每个类别会触发 $n \times k$ 个特征中的 n 个，这 n 个特征的加权和经过 Softmax，代表输入被分到各类的概率。
把最大熵模型写成如下的形式：
\[P_w(y|\overrightarrow{x}) = \frac{\exp\left \{ \overrightarrow{w } \cdot f (\overrightarrow{x},y) \right \}}{\sum _y \exp \left \{ \overrightarrow{w } \cdot f(\overrightarrow{x},y) \right \}}\]
当判断数据是否属于类别 k 时相互转换时，直接把特征函数设计成如下的形式：
\[f(\overrightarrow{x},y) = \left \{ \begin{aligned}
&\overrightarrow{x}, \ y = k \\
&0, \ else
\end{aligned} \right . \]
则可以得到以下的形式 ，下式的 $\overrightarrow{w}$ 对应参数只有 n 维 不等于 0 ：
\[P_w(y = k|\overrightarrow{x}) = \frac{\exp\left \{ \overrightarrow{w} \cdot \overrightarrow{x} \right \}}{\sum _y \exp \left \{ \overrightarrow{w} \cdot \overrightarrow{x} \right \}}\]
一般的机器学习任务中，不用像在 NLP 中需要对文本提取特征，机器学习任务中的输入 $\mathbf{x}$ 一般是数字向量的形式，所以使用起来比 MaxEnt 灵活； 但是 MaxEnt 模型在 NLP 任务中对于一个词可以抽取多种特征，比如说他的前缀，后缀，词性等等，所以特征设计更加灵活，这也是 CRF 的一个特点，以前不理解为什么 CRF++ 在分词时可以为每个字设置多个特征，现在理解一些了，还有老师木也说过：“Logistic 与 MaxEnt 与 CRF 其实就是一个东西”，现在对这句话也有了点理解，对于 MaxEnt 模型可以提取多种特征的形式只不过是在图模型的基础上多加几组因子而已。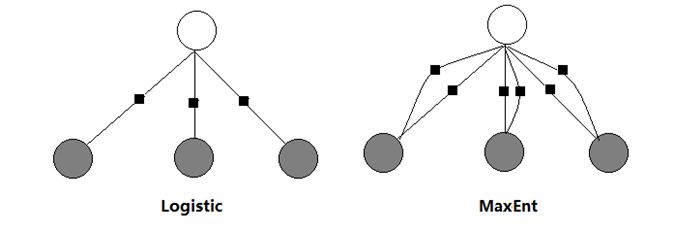
朴素贝叶斯
朴素贝叶假设给定类别时，特征之间条件独立的：
\[p(y|\overrightarrow{x}) \propto p(y,\overrightarrow{x}) = p(y)\prod_{i=1}^np(x_i|y)\]
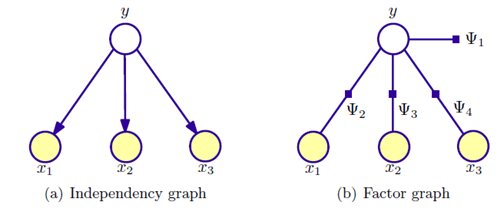
Navie Bayes 的图模型表示：
\[P(x_1,x_2,x_3,y) = p(y)p(x_1|y)p(x_2|y)p(y_3|y)\]
因子图表示为：
\[P(x_1,x_2,x_3,y) = \Psi_1(y)\Psi_2(x_1,y)\Psi_3(x_2,y)\Psi_4(y_3,y)\]
HMM 模型
在 Navie Bayes 中，是对单个元素 y 进行预测，当预测变量也为序列时，模型变为：
\[p(\overrightarrow{x},\overrightarrow{y}) =\prod_{i=0}^n p(y_i|y_{i-1}) p(x_i|y_i)\]
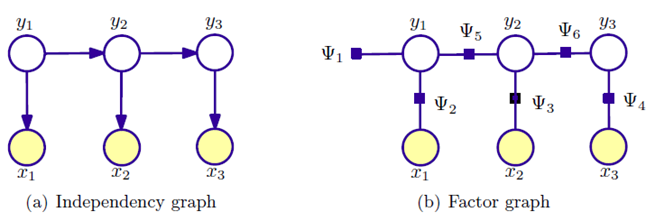
HMM 的图模型表示：
\[P(x_1,x_2,x_3,y_1,y_2,y_3) = p(y_1)p(x_1|y_1)p(y_2|y_1)p(x_2|y_2)p(y_3|y_2)p(x_3|y_3)\]
因子图表示类似，这里不再赘述
MaxEnt 模型：
这里给出一个一般形式下的最大熵模型，最大熵或者 Logistic 的形式是对条件概率进行建模的：
\[P(y|x) = \frac{\exp\left \{ \sum_k w_k \cdot f_k(x,y) \right \}}{\sum _y \exp \left \{ \sum_k w_k f_k(x,y) \right \}}\]
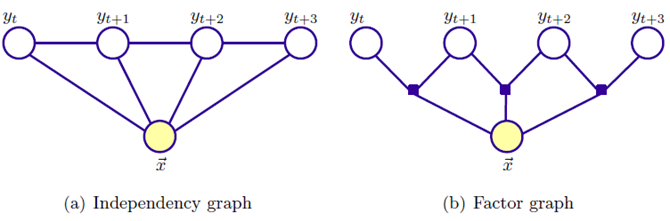
下图给出了一个随机变量 x 的情况下 Maxent 的图模型表示，图 (b) 三个约束表示三组势函数，这便是相对于 Logistic 的优势了，可以提取多组特征：
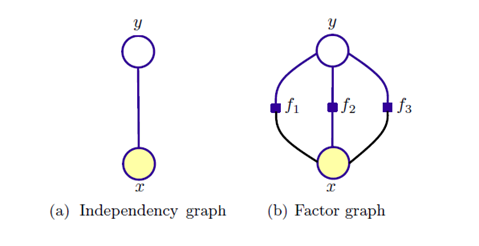这里并不能像有向图那样表示成精确的概率形式，而只能表示成最大团上的一组势能函数的形式。 MaxEnt 模型可以在 x 与 y 之间设置任意多的特征函数，这样会综合考虑各种特征信息。
CRF 的模型：
CRF 是 MaxEnt 模型序列化的推广：
\[\begin{aligned} P(y|x) &= \frac{\exp \left \{ \sum_{k=1}^K w_k f_k(y,x) \right \}}{\sum_y \exp \left \{ \sum_{k=1}^Kw_kf_k(y,x)\right \}}\end{aligned} \]
总结：
HMM模型： 将标注看作马尔可夫链，一阶马尔可夫链式针对相邻标注的关系进行建模，其中每个标记对应一个概率函数。HMM是一种生成模型，定义了联 合概率分布 ，其中 x 和 y 分别表示观察序列和相对应的标注序列的随机变量。为了能够定义这种联合概率分布，生成模型需要枚举出所有可能的观察序列，这在实际运算过程中很困难，因为我们需要将观察序列的元素看做是彼此孤立的个体即假设每个元素彼此独立，任何时刻的观察结果只依赖于该时刻的状态。
HMM 模型的这个假设前提在比较小的数据集上是合适的，但实际上在大量真实语料中观察序列更多的是以一种多重的交互特征形式表现，观察序列之间广泛存在长程相关性。在命名实体识别的任务中，由于实体本身结构所具有的复杂性，利用简单的特征函数往往无法涵盖所有的特性，这时HMM的假设前提使得它无法使用复杂特征 （无法使用多于一个标记的特征）。
MaxEnt 模型： 可以使用任意的复杂相关特征，在性能上最大熵分类器超过了 Byaes 分类器。但是，作为一种分类器模型，这两种方法有一个共同的缺点：每个词都是单独进行分类的，标记之间的关系无法得到充分利用，具有马尔可夫链的 HMM 模型可以建立标记之间的马尔可夫关联性，这是最大熵模型所没有的。
最大熵模型的优点：首先，最大熵统计模型获得的是所有满足约束条件的模型中信息熵极大的模型；其次，最大熵统计模型可以灵活地设置约束条件，通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合程度；再次，它还能自然地解决统计模型中参数平滑的问题。
最大熵模型的不足：首先，最大熵统计模型中二值化特征只是记录特征的出现是否，而文本分类需要知道特征的强度，因此，它在分类方法中不是最优的;其次，由于算法收敛的速度较慢，所以导致最大熵统计模型它的计算代价较大，时空开销大;再次，数据稀疏问题比较严重。
CRF 模型：首先，CRF 在给定了观察序列的情况下，对整个的序列的联合概率有一个统一的指数模型。一个比较吸引人的特性是其为一个凸优化问题。其次，条件随机场模型相比改进的隐马尔可夫模型可以更好更多的利用待识别文本中所提供的上下文信息以得更好的实验结果。并且有测试结果表明：在采用相同特征集合的条件下，条件随机域模型较其他概率模型有更好的性能表现。
CRF 具有很强的推理能力，并且能够使用复杂、有重叠性和非独立的特征进行训练和推理，能够充分地利用上下文信息作为特征，还可以任意地添加其他外部特征，使得模型能够 获取的信息非常丰富。
CRF 模型的不足：首先，通过对基于 CRF 的结合多种特征的方法识别英语命名实体的分析，发现在使用 CRF 方法的过程中，特征的选择和优化是影响结果的关键因 素，特征选择问题的好与坏，直接决定了系统性能的高低。其次，训练模型的时间比 MaxEnt 更长，且获得的模型很大，在一般的 PC 机上无法运行。
参考：(6,7 是两篇非常经典的 CRF toturial)
1. https://www.zhihu.com/question/35866596
2. http://blog.csdn.net/losteng/article/details/51037927
3. https://www.zhihu.com/question/24094554/answer/108247115
4. http://www.cnblogs.com/ooon/p/5690848.html
5. the equivalence of logistic regression and maximum entropymodels
6. An Introduction to Conditional Random Fields
7. Classical Probabilistic Models and Conditional Random Fields
