CS224N Lecture 2
Word Vectors, Word Senses, and Neural Network Classifiers
Lecture Plan
- Course organization
- Finish looking at word vectors and word2vec
- Optimization basics
- Can we capture the essence of word meaning more effectively by counting?
- The GloVe model of word vectors
- Evaluating word vectors
- Word senses
- Review of classification and how neural nets differ
- Introducing neural networks
Key Goal: To be able to read word embeddings papers by the end of class
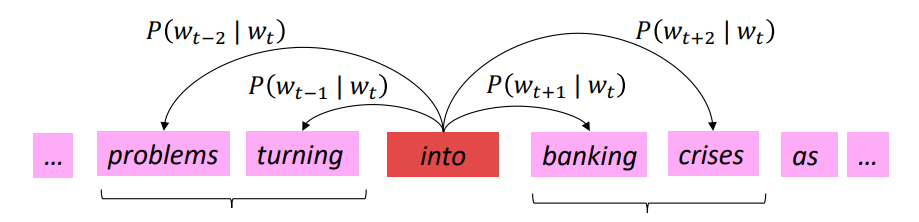
Review: Main idea of word2vec
- 从随机词向量开始
- 遍历整个语料库中的每个单词
- 使用词向量预测周围的单词:
\[P(o|c) = \frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)} \]
- 更新词向量,以便可以更好地预测实际周围的词
- 只做这个简单的算法,该算法学习的词向量可以很好地捕捉单词空间中的单词相似性和有意义的方向
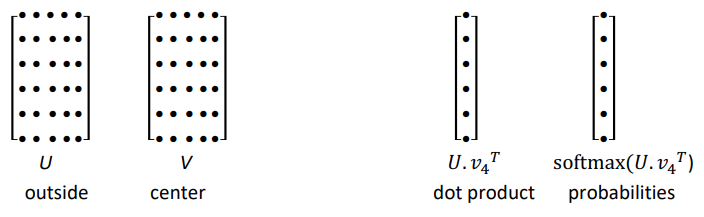
Word2vec parameters and computations
\[(n, d) \cdot (d, 1) \rightarrow (n, 1) \overset{softmax} \to (n, 1) \]该模型实际上并不关注词序或位置,无论在中心词旁边,还是在左侧或右侧稍远一点都没关系,概率估计将是相同的。
Word2vec maximizes objective function by putting similar words nearby in space
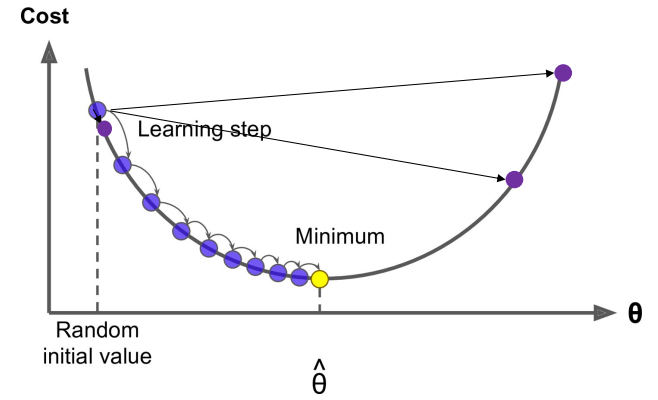
Optimization: Gradient Descent
- 为了学习好的词向量:有一个代价函数 \(J(\theta)\) 需要最小化
- 梯度下降是一种通过改变 \(\theta\) 来最小化 \(J(\theta)\) 的算法
- Idea:从当前的 \(\theta\) 值,计算(粗略估计)出 \(J(\theta)\) 的梯度,然后向负梯度方向迈出一小步,重复上述过程
Gradient Descent
- 更新方程(用矩阵表示):
\[\theta^{new} = \theta^{old} - \alpha\nabla_{\theta}J(\theta) \]
- 更新方程(对于单个参数):
\[\theta_j^{new} = \theta_j^{old} - \alpha\frac{\partial}{\partial \theta_j^{old}}J(\theta) \]
- 算法:
while True: theta_grad = evaluate_gradient(J, corpus, theta) theta = theta - alpha * theta_grad
Stochastic Gradient Descent
- Problem: \(J(\theta)\) 是语料库中所有窗口的函数
- 所以 \(\nabla_{\theta}J(\theta)\) 计算起来非常昂贵
- 在进行一次更新之前,会等待很长时间
- Solution:Stochastic Gradient Descent (SGD)
- 重复采样窗口,并在每个窗口或每个小批量后更新
- 算法:
while True: window = sample_window(corpus) theta_grad = evaluate_gradient(J, window, theta) theta = theta - alpha * theta_grad
Stochastic gradients with word vectors![Aside]
- 在每个这样的窗口迭代地获取梯度用于 SGD
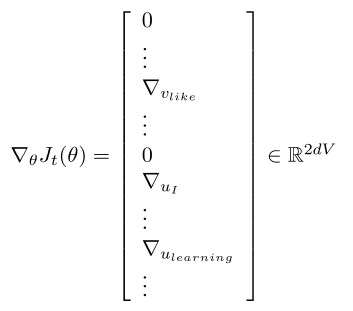
- 但是在每个窗口中,我们最多只有 \(2m + 1\) 个单词,所以 \(\nabla_{\theta}J_t(\theta)\) 非常稀疏
Stochastic gradients with word vectors!
- 我们可能只更新实际出现的词向量
- Solution:要么需要稀疏矩阵更新操作来仅更新完整嵌入矩阵 \(U\) 和 \(V\) 的某些行,要么需要为词向量保留一个散列
- 如果有数百万个词向量并进行分布式计算,那么避免发送大量更新非常重要
Word2vec algorithm family: More details
为什么两个向量?
- 更容易优化,最后都取平均值
- 可以每个单词只用一个向量
两个模型变体
- Skip-grams (SG)
- 输入中心词并预测上下文中的单词
- Continuous Bag of Words (CBOW)
- 输入上下文中的单词并预测中心词
提高训练效率:
- Negative sampling
- 之前一直使用naive的softmax(简单但代价很高的训练方法),使用负采样方法加快训练速率
The skip-gram model with negative sampling (HW2)
- softmax中用于归一化的分母的计算代价太高
\[P(o|c) = \frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)} \]
- 因此,在标准 word2vec 和 HW2 中,使用负采样实现 skip-gram 模型
- Main idea:使用一个 true pair (中心词及其上下文窗口中的词)与几个 noise pair (中心词与随机词搭配) 形成的样本,训练二元逻辑回归
- (最大化)目标函数:
\[J(\theta)=\frac{1}{T} \sum_{t=1}^{T} J_{t}(\theta) \]\[J_{t}(\theta)=\log \sigma\left(u_{o}^{T} v_{c}\right)+\sum_{i=1}^{k} \mathbb{E}_{j \sim P(w)}\left[\log \sigma\left(-u_{j}^{T} v_{c}\right)\right] \]
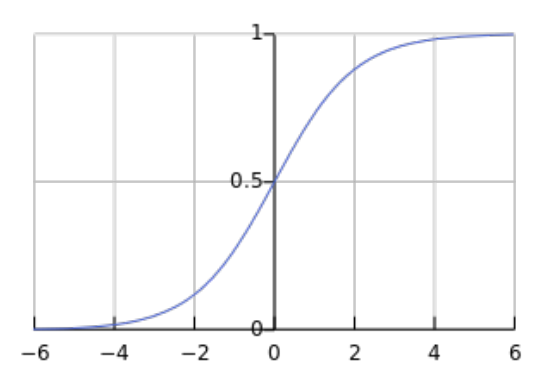
- sigmoid:
\[\sigma(x)=\frac{1}{1 + e^{-x}} \]
- 最大化两个词在第一个 log 中同时出现的概率并最小化噪声词的概率
更加贴近 HW2 的目标函数:\[J_{neg-sample}(u_o, v_c, U)=-\log\sigma(u_o^Tv_c)-\sum_{k \in \{K\, sampled\, indices\}} \log\sigma(-u_k^Tv_c) \]
- k是负采样的样本数目
- 最大化中心词与真实上下文单词的向量点积,最小化中心词与随机单词的点积
\[P(w)=U(w)^{3 / 4} / Z \]使用上式作为抽样的分布,\(U(w)\) 是 unigram 分布,通过 \(\frac{3}{4}\) 次方,相对减少常见单词的频率,增大稀有词的概率。 \(Z\) 用于生成概率分布。
Why not capture co-occurrence counts directly?
构建一个共现矩阵 X
- 两个选项:windows vs. full document
- Window:类似于 word2vec,在每个单词周围使用 window \(\rightarrow\) 捕获一些句法和语义信息
- Word-document 共现矩阵的基本假设是在同一篇文章中出现的单词更有可能相互关联。假设单词 \(i\) 出现在文章 \(j\) 中,矩阵元素 \(X_{ij}\) 加一,矩阵 \(X\) 的大小为 \(|V| \times M\),\(|V|\) 为词汇量,\(M\) 为文章数。这一构建单词文章co-occurrence matrix的方法也是经典的Latent Semantic Analysis所采用的。
Example: Window based co-occurrence matrix
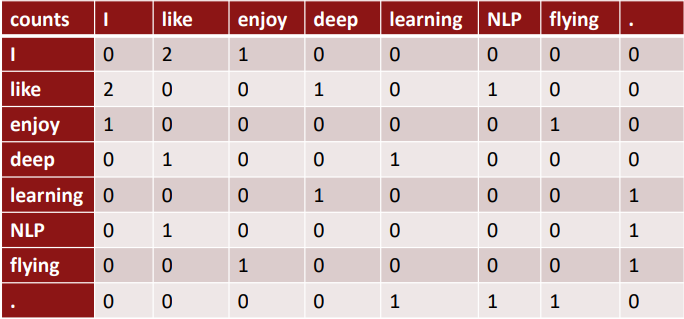
利用某个定长窗口中单词与单词同时出现的次数来产生 window-based (word-word) co-occurrence matrix。下面以窗口长度为1来举例,假设我们的数据包含以下几个句子:
- I like deep learning
- I like NLP
- I enjoy flying
Co-occurrence vectors
- Simple count co-occurrence vectors
- 向量大小随着词汇表大小增长
- 维度高,需要很大的存储空间
- 后续分类模型有稀疏性、随机性问题 -> 模型鲁棒性较低
- Low-dimensional vectors
- Idea: 存储更多重要信息在少数维度 -> 稠密向量
- 通常 25-1000 维
- 如何降低计数共现维度?
Classic Method: Dimensionality Reduction on X(HW1)
奇异值分解(SVD) -> \(X = U \sum V^T\), \(\sum\) 是对角线矩阵,对角线上的值是矩阵的奇异值,\(U, V\) 是对应于行和列的正交基。
为了减少维度同时尽量保存有效信息,可保留对角矩阵的最大的 \(k\) 个值,并将 \(U, V\) 相应的行列保留。
这种经典的线性代数方法,对于大型矩阵,计算的代价昂贵。
Hacks to X(several used in Rohde et al.2005 in COALS)
按比例调整 counts 是有效的
- 对高频词进行缩放
- log 缩放
- \(min(X, t), t \approx 100\)
- 忽视高频词
- 基于window的计数,提高更接近单词的计数
- 使用Person相关系数
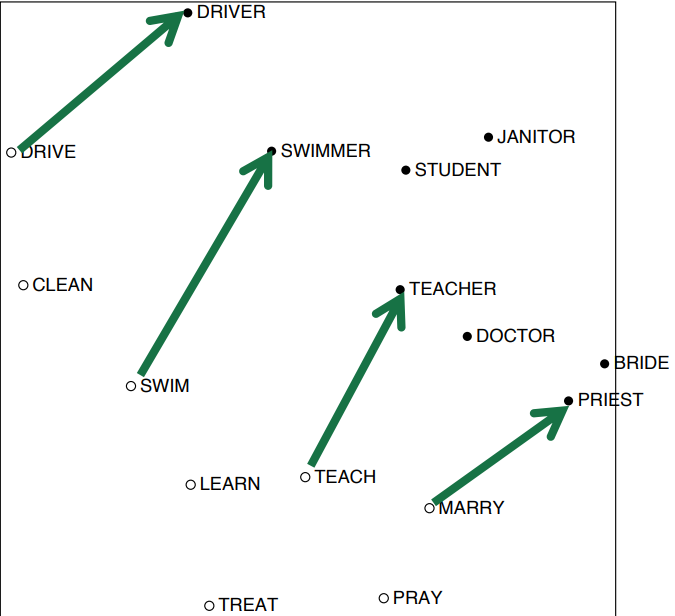
Interesting semantic patterns emerge in the scaled vectors
\(drive \rightarrow driver, swim \rightarrow swimmer, teach \rightarrow teacher\)
在向量中出现的有趣的句法模式:语义向量基本上是线性组件,虽然有一些摆动,但是基本是存在动词和动词实施者的方向。
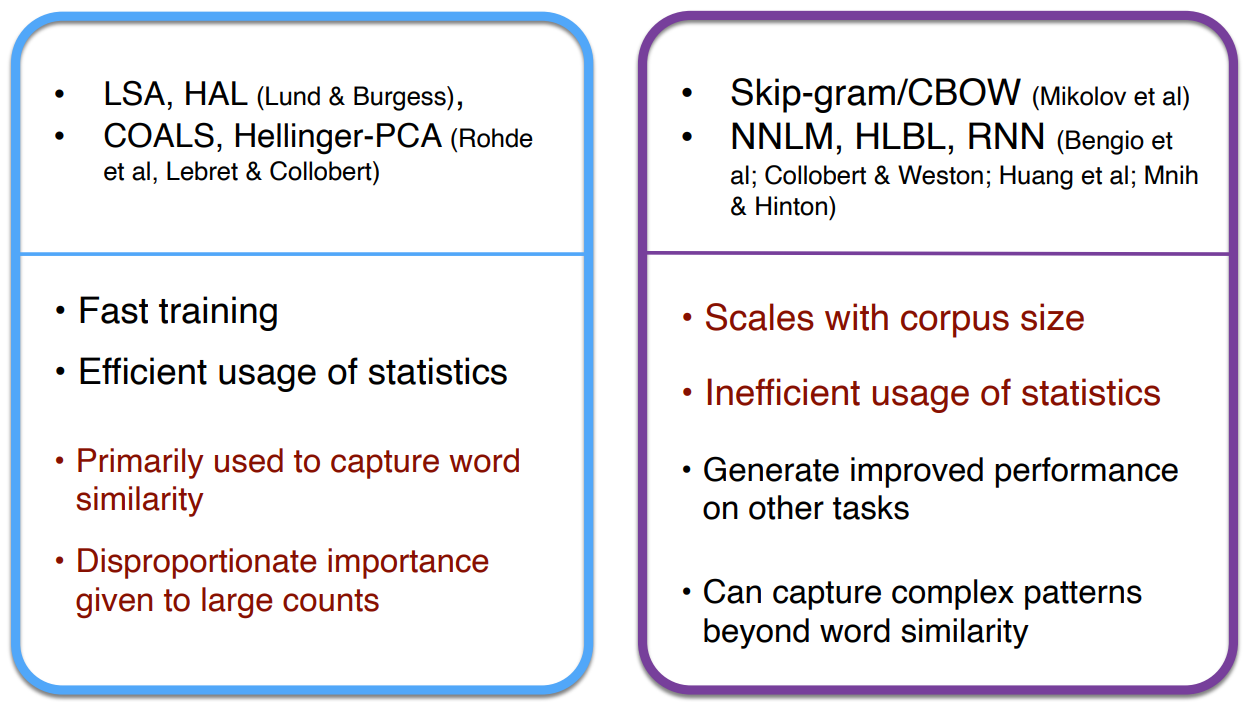
Towards GloVe: Count based vs. direct prediction
基于计数:使用整个矩阵的全局统计数据来直接估计
- 优点:
- 训练快
- 高效利用统计数据
- 缺点:
- 用于捕捉单词相似性
- 对大量数据给予比例失调的重视
转换计数:定义概率分布并试图预测单词
- 优点:
- 提高其他任务的性能
- 能捕获除了单词相似性以外的复杂的模式
- 缺点:
- 与语料库大小有关的量表
- 统计数据的低效利用(采样是对统计数据的低效利用)
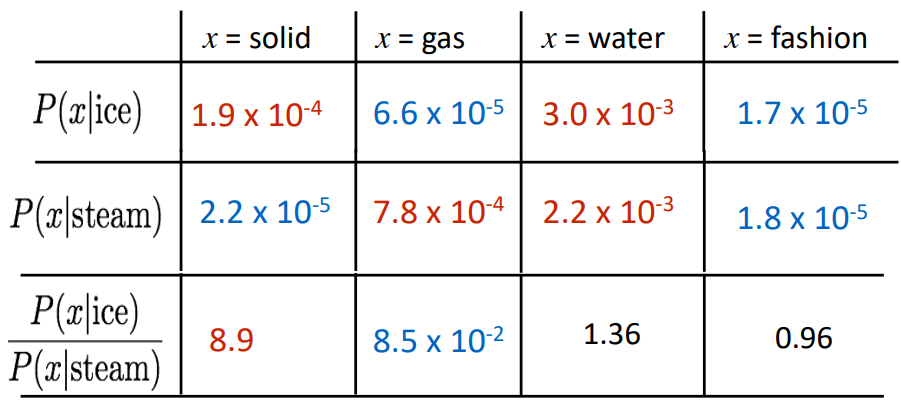
Encoding meaning components in vector differences
关键思想:共现概率的比值可以对meaning component进行编码
重点不是单一的概率大小,重点是他们之间的比值,其中蕴含着meaning component。
如何在词向量空间中以线性meaning component的形式捕获共现概率的比值?
Log-bilinear model: \(w_i \dot w_j = logP(i | j)\)
with vector differences: \(w_x \dot (w_a - w_b) = log\frac{P(x | a)}{P(x | b)}\)
Combining the best of both worlds
\[w_i \dot w_j = logP(i | j) \]\[J=\sum_{i, j=1}^{V} f\left(X_{i j}\right)\left(w_{i}^{T} \tilde{w}_{j}+b_{i}+\tilde{b}_{j}-\log X_{i j}\right)^{2} \]


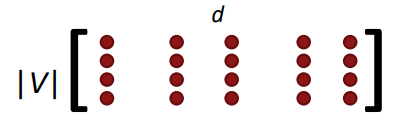
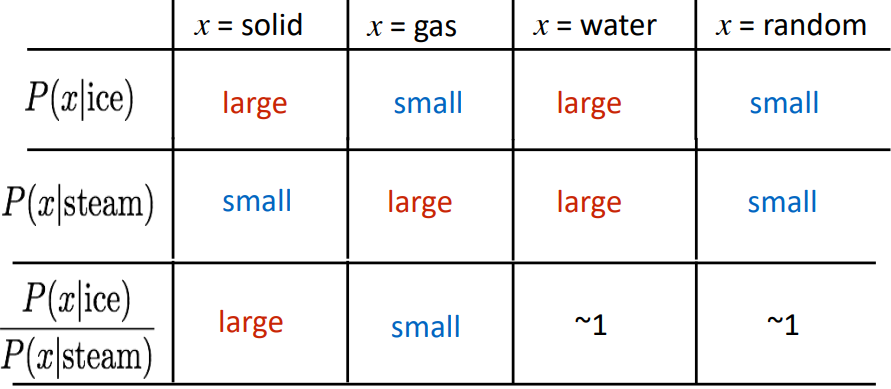

 浙公网安备 33010602011771号
浙公网安备 33010602011771号