![image]()
贪心题单
接下来我将按顺序一个个讲解我的做题思路
注意每个题都有折叠代码!!!
P1614 爱与愁的心痛
![image]()
很简单的一个入门题,因为它想要连续m个数和最小,那么我们遍历一遍数组,每次答案更新为最小答案即可。注意有n为0的情况,此时特判答案为0。
点击查看代码
signed main()
{
int n,m,res=1e9,sum=0;
cin>>n>>m;
if(n==0) {
cout<<0;
return 0;
}
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
sum+=a[i];
if(i>=m) {
sum-=a[i-m];
res=min(res,sum);
}
}
cout<<res;
}
P1803 凌乱的yyy / 线段覆盖
![image]()
首先我们知道右端点的大小会决定能不能参加下一场比赛,如果一把比赛结束时间很晚而相反同一起始时间我们有结束早点的比赛,那么我们肯定会选择结束早的比赛。所以我们按右端点排序,优先选择右端点小的比赛。
点击查看代码
signed main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].second>>a[i].first;
}
sort(a+1,a+n+1);
int id=0,res=0;
for(int i=1;i<=n;i++){
if(a[i].second>=id){
res++,id=a[i].first;
}
}
cout<<res;
}
P1090 [NOIP2004 提高组] 合并果子
![image]()
比较经典的题目,我们每次选择两个消耗体力最小的进行合并,因为我们合并完的以后再合并时会多合并几次,而我们合并总次数是有限的,所以我们优先选择小的合并。开一个小根堆遍历一遍就能完美解决了。
点击查看代码
signed main()
{
priority_queue<int,vector<int>,greater<int>> q;
int n;
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
q.push(x);
}
int res=0;
while(q.size()>1)
{
int x=q.top();
q.pop();
int y=q.top();
q.pop();
res+=x+y;
q.push(x+y);
}
cout<<res;
}
P1190 [NOIP2010 普及组] 接水问题
![image]()
本来感觉是个和贪心扯不太上边的题目,就是一个模拟。后来听了讲解发现了一个新的贪心思路。我们对于每个水龙头下都初始安排一个人,然后肯定是接水快的先让下一个人换过来。那么我们开一个小根堆,初始存m个人,然后对m+1开始遍历数组,每次我们从堆里取最小的数,那个肯定是最先接完水的,我们把那个人加进去,比如1,2我们就会获得一个3。最后我们取堆底的最大值即可。
点击查看代码
signed main()
{
int n,m;
priority_queue<int,vector<int>,greater<int>> q;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
if(i<=m) q.push(a[i]);
}
for(int i=m+1;i<=n;i++){
int c=q.top();
q.pop();
q.push(c+a[i]);
}
int res=0;
while(q.size()){
res=max(res,q.top());
q.pop();
}
cout<<res;
}
P7427 [THUPC2017] 玩游戏
![image]()
我们知道1+2+3...+n=a+b,根据等差数列求和,a+b=n*(n+1)/2。
![image]()
所以我们可以用这样一个思路算出n,或者从1加到和等于a+b时暴力遍历算出n。于是我们知道当n*(n+1)/2不等于a+b时是NO。其余情况,我们只要在n的排列中选择一些数让它们总和等于a即可。在这里有一个结论,就是我们从n开始往1遍历,每次能减则减,最后肯定能得到a。
点击查看代码
signed main()
{
int a,b;
cin>>a>>b;
int sum=a+b;
int n=sqrt(2*sum);
if(n*(n+1)/2!=sum) cout<<"NO";
else{
cout<<n;
for(int i=n;i>=1;i--)
{
if(a>=i) {
cout<<" "<<i;
a-=i;
}
}
}
}
P1684 考验
![image]()
我们不难发现,前三个韵脚其实就是两个A和两个B的任意组合。我们考虑可以用map纪录下已经出现的数字个数,当map[x]==2时,我们相当于获得了一个两个A,也就是说我们只要再获得一个两个B就能得到一个答案。所以我们从前往后遍历,每次能组合时就组合,然后因为每次组合相当于组合那一段全部清空,于是我们就把目前得到的数字个数清空,继续遍历即可。为什么得到答案就加,那是因为我们就往后走浪费掉的AB就越多,并且我们AB任意组合都是可以得到答案的,所以就算再往后走也不会有更优组合情况,于是我们可以得出贪心正确的结论。
点击查看代码
signed main()
{
int n,num=0,res=0;
map<int,int> mp;
cin>>n;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
mp[x]++;
if(mp[x]==2) num++;
if(mp[x]==4||num==2){
num=0;
mp.clear();
res++;
}
}
cout<<res;
}
P6878 [JOI 2020 Final] JJOOII 2
![image]()
这个题我们这么想,我们其实只要确认了前K个J,后面的O和I就都确定出来了。所以我们枚举所有可能的J的位置,然后就可以推出这个串的最终位置,那么我们就可以算出在一个长度确定的子串里保留3*k个数要删掉数的答案,然后每次更新最小值即可。
点击查看代码
signed main()
{
string s;
int n,k;
cin>>n>>k>>s;
vector<int> idj,ido,idi;
for(int i=0;i<n;i++)
{
if(s[i]=='J') idj.push_back(i);
else if(s[i]=='O') ido.push_back(i);
else idi.push_back(i);
}
int numj=idj.size()-1,numo=ido.size()-1,numi=idi.size()-1;
int sto=0,sti=0,res=1e9;
for(int i=0;i<=numj-k+1;i++)
{
int end=idj[i+k-1];
while(ido[sto]<=end&&sto<=numo) sto++;
if(sto+k-1>numo) break;
end=ido[sto+k-1];
while(idi[sti]<=end&&sti<=numi) sti++;
if(sti+k-1>numi) break;
end=idi[sti+k-1];
res=min(res,end-idj[i]+1-3*k);
}
if(res==1e9) cout<<-1;
else cout<<res;
}




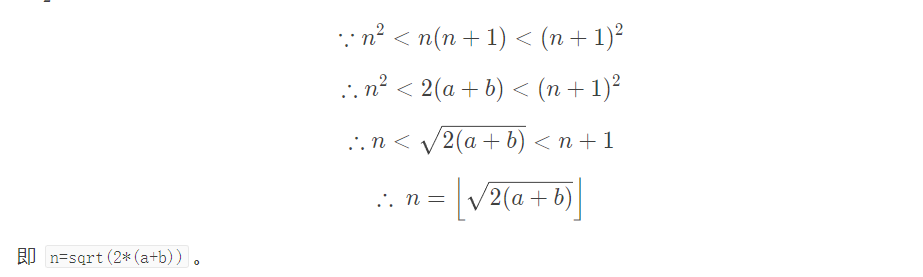






 浙公网安备 33010602011771号
浙公网安备 33010602011771号