树到云端

树到云端

给定一棵边权为 $1$，由 $n$ 个节点构成的树，第 $i$ 个点的点权为 $\text{val}_i$，设 $\text{dis}(i,j)$ 表示点 $i$ 到点 $j$ 的最短距离（特别地，$\text{dis}(i,i) = 0$），记 $t_i = \sum\limits_{j=1}^{n}{\text{val}_j \times \text{dis}(i,j)}$。

现在给定树的结构和 $t$ 数组，要求求出 $\text{val}$ 数组，（数据保证 $\text{val}_i$ 均为正整数）。

输入描述:

第一行输入一个整数 $n$ $(2 \leq n \leq 6 \times 10^5)$

此后 $n-1$ 行，第 $i$ 行输入两个整数 $u_i,v_i$ $(1 \leq u_i,v_i \leq n)$ 表示第 $i$ 条树边连接节点 $u_i$ 和节点 $v_i$。

第 $n+1$ 行输入 $n$ 个整数 $t_1,t_2,\ldots,t_n$ $(1 \leq t_i \leq 10^9)$ 代表给定的数组。

$n$
$u_1$ $v_1$
$u_2$ $v_2$
$\vdots$
$u_{n-1}$ $v_{n-1}$
$t_1$ $t_2$ $t_3$ $\ldots$ $t_n$

输出描述:

在一行上输出 $n$ 个正整数 $\text{val}_1,\text{val}_2,\ldots,\text{val}_n$，第 $i$ 个整数表示节点 $i$ 的点权。

示例1

输入

2
1 2
1 3

输出

3 1

示例2

输入

5
1 2
1 3
1 4
1 5
18 40 40 24 28

输出

6 1 1 9 7

示例3

输入

5
1 2
1 3
3 4
4 5
34 40 34 40 56

输出

3 9 3 5 4

 

解题思路

  以为是构造，推着推着发现是解方程，但只知道其中 $n-1$ 个等式另外一个不知道怎么构造。并且实际上并不需要高斯消元。

  我们假定节点 $1$ 为树根。假设我们知道了 $t_u$，考虑其某个儿子 $v$ 的 $t_v$ 是如何通过 $t_u$ 调整得到。从 $t_u$ 到 $t_v$ 的变化是，从 $u$ 到每个节点的距离变成了 $v$ 到每个节点的距离，因此我们只需考虑距离的变化即可。为了方便我们可以把 $u$ 换成根，如下图所示：

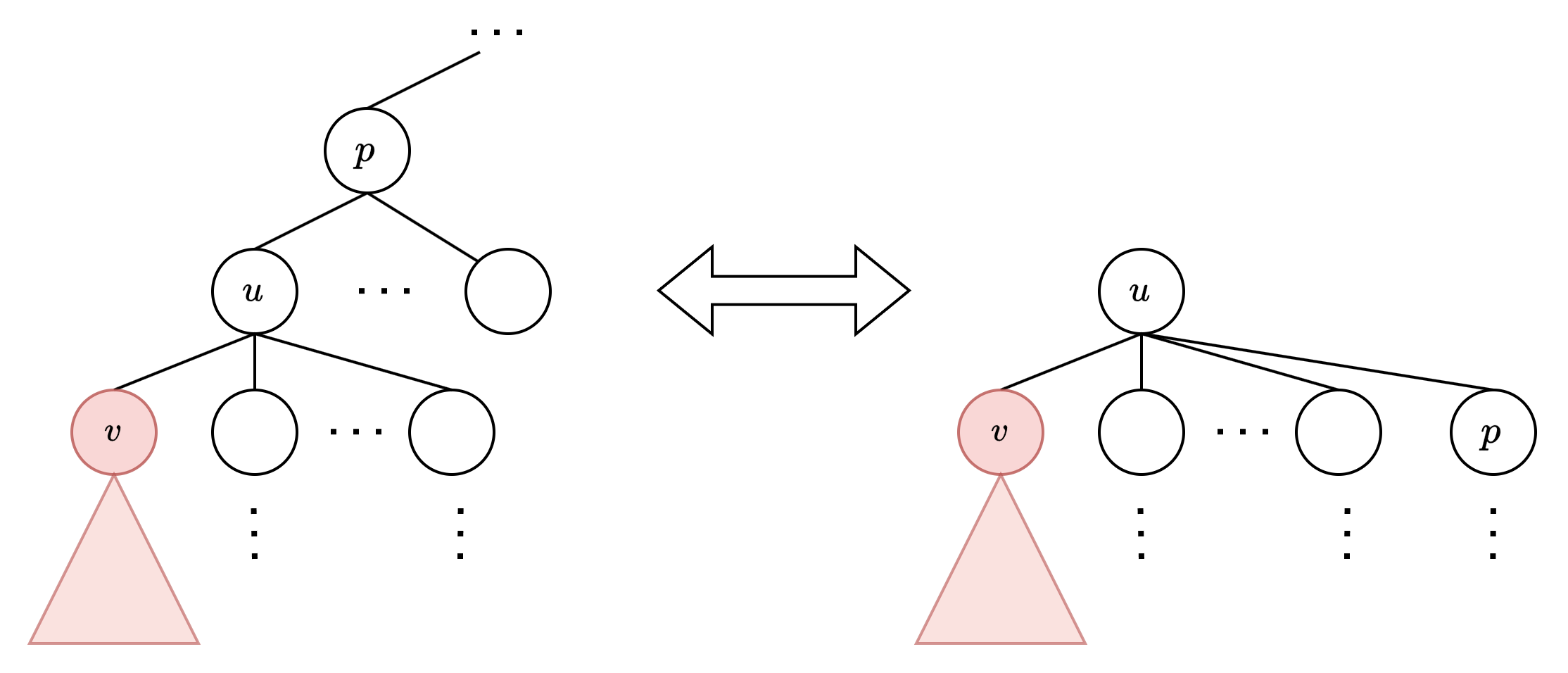
  为了得到 $t_v$ 我们把 $v$ 换成根，在这个过程中考虑每个节点从到 $u$ 的距离变成到 $v$ 的距离变化，其中对于子树 $v$ 内的每个节点（红色部分）其距离会减少 $1$，而其余节点的距离会增加 $1$。记 $s_u$ 表示子树 $u$ 中每个节点的 $\text{val}$ 的和，因此有 $t_u -s_v + s_1 - s_v = t_v \Rightarrow s_1 - 2s_v = t_v - t_u$，$s_1$ 相当于整棵树的 $\text{val}$ 之和。由于每条边都对应一条该等式，所以一共有 $n-1$ 条（线性无关），然而一共有 $n$ 个未知量 $s_i \, (1 \leq i \leq n)$，因此我们还需要找到另外一条等式。

  我们先把 $n-1$ 条等式给加起来，得到 $(n-1)s_1 - 2\sum\limits_{i=2}^{n}{s_i} = \sum\limits_{(u,v) \in E}{t_v - t_u}$，其中 $\sum\limits_{(u,v) \in E}{t_v - t_u}$ 可以枚举每条边计算得到，现在的问题是如何将 $\sum\limits_{i=2}^{n}{s_i}$ 变成与 $s_1$ 相关的式子，从而求出 $s_1$，进而通过等式 $s_1 - 2s_v = t_v - t_u$ 求出其余的 $s_v$。

  $\sum\limits_{i=2}^{n}{s_i}$ 本质上由每个节点的 $\text{val}_v$ 的倍数构成，这个倍数就是包含节点 $v$ 的子树数量，而包含 $v$ 的子树数量就是 $v$ 的祖先节点数量，$v$ 的祖先节点数量就是 $1$ 到 $v$ 的距离。因此有 $\sum\limits_{i=2}^{n}{s_i} = \sum\limits_{i=2}^{n}{\text{val}_i \times \text{dis}(1,i)} = \sum\limits_{i=1}^{n}{\text{val}_i \times \text{dis}(1,i)} = t_1$。

  因此就有 $s_1 = \dfrac{\left(\sum\limits_{(u,v) \in E}{t_v - t_u} \right) + 2t_1}{n-1}$，$s_i = \dfrac{s_1 - t_i + t_{\text{fa}_i}}{2} \, (2 \leq i \leq n)$，其中 $\text{fa}_i$ 表示 $i$ 的父节点。从而有 $\text{val}_i = s_i - \sum\limits_{v \in \text{son}(i)}{s_v}$。

  AC 代码如下，时间复杂度为 $O(n)$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 6e5 + 5, M = N * 2;

int h[N], e[M], ne[M], idx;
int t[N], fa[N], s[N];

void add(int u, int v) {
    e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

LL dfs(int u, int p) {
    fa[u] = p;
    LL s = 0;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int v = e[i];
        if (v == p) continue;
        s += dfs(v, u) + t[v] - t[u];
    }
    return s;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    memset(h, -1, sizeof(h));
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        add(u, v), add(v, u);
    }
    for (int i = 1; i <= n; i++) {
        cin >> t[i];
    }
    s[1] = (dfs(1, 0) + 2 * t[1]) / (n - 1);
    for (int i = 2; i <= n; i++) {
        s[i] = s[1] - t[i] + t[fa[i]] >> 1;
    }
    for (int i = 1; i <= n; i++) {
        int ret = s[i];
        for (int j = h[i]; j != -1; j = ne[j]) {
            int v = e[j];
            if (v != fa[i]) ret -= s[v];
        }
        cout << ret << ' ';
    }
    
    return 0;
}

 

参考资料

  牛客练习赛139 题解：https://blog.nowcoder.net/n/abde3d8eb296416ba533e35df608dcb3