C. Envy

For a connected undirected weighted graph $G$, MST (minimum spanning tree) is a subgraph of $G$ that contains all of $G$'s vertices, is a tree, and sum of its edges is minimum possible.

You are given a graph $G$. If you run a MST algorithm on graph it would give you only one MST and it causes other edges to become jealous. You are given some queries, each query contains a set of edges of graph $G$, and you should determine whether there is a MST containing all these edges or not.

Input

The first line contains two integers $n, m$ $(2 \leq n, m \leq 5 \cdot 10^5, n - 1 \leq m)$ — the number of vertices and edges in the graph and the number of queries.

The $i$-th of the next $m$ lines contains three integers $u_i$, $v_i$, $w_i$ $(u_i \ne v_i, 1 \leq w_i \leq 5 \cdot 10^5)$ — the endpoints and weight of the $i$-th edge. There can be more than one edges between two vertices. It's guaranteed that the given graph is connected.

The next line contains a single integer $q$ $(1 \leq q \leq 5 \cdot 10^5)$ — the number of queries.

$q$ lines follow, the $i$-th of them contains the $i$-th query. It starts with an integer $k_i$ $(1 \leq k_i \leq n - 1)$ — the size of edges subset and continues with $k_i$ distinct space-separated integers from $1$ to $m$ — the indices of the edges. It is guaranteed that the sum of $k_i$ for $1 \leq i \leq q$ does not exceed $5 \cdot 10^5$.

Output

For each query you should print "YES" (without quotes) if there's a MST containing these edges and "NO" (of course without quotes again) otherwise.

Example

Input

Output

YES
NO
YES
NO

Note

This is the graph of sample:

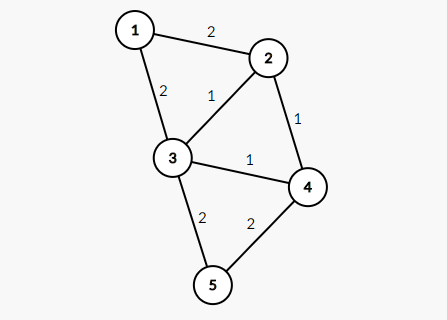
Weight of minimum spanning tree on this graph is $6$.

MST with edges $(1, 3, 4, 6)$, contains all of edges from the first query, so answer on the first query is "YES".

Edges from the second query form a cycle of length $3$, so there is no spanning tree including these three edges. Thus, answer is "NO".

解题思路

在讲解本题做法之前，首先证明一个性质。

性质：对于同一个无向图，在 Kruskal 算法执行过程中，当处理完所有权值小于某个值的边后，图的连通分量结构（各连通分量的节点组成）是唯一的，与处理同权值边的顺序无关。

证明：采用数学归纳法，对边权值 $w$ 进行归纳。当 $w = 0$ 时，初始状态为每个节点均为独立的连通分量，此时尚未加入任何边，显然成立。假设在处理完所有边权小于 $w$ 的边后，图的连通分量结构唯一确定。现在我们证明处理完边权等于 $w$ 的边后，连通分量结构仍唯一确定。

设当前已处理完边权小于 $w$ 的边，得到连通分量集合 $\mathcal{C} = \{C_1, C_2, \ldots, C_m \}$。令 $E_w$ 为所有权值等于 $w$ 的边构成的集合，根据 Kruskal 算法需从中选出能连接不同连通分量的边，对应的边集为 $E_w'=\{ (u,v,w) \in E_w \mid \text{端点 } u,v \text{ 属于 } \mathcal{C} \text{ 中不同的连通分量} \}$。$E_w'$ 中的边可看作以 $\mathcal{C}$ 为点集的图 $H$ 中的边，其中每条边连接两个不同节点（连通分量）。根据 Kruskal 算法，选择的边需构成 $H$ 的最大生成森林（即无环且最大化边数）。

若 $E_w'$ 中无边形成环，此时 $H$ 仍为森林，按任意顺序加入 $E_w'$ 中的边都不会形成环，最终连通分量由 $H$ 的连通性决定，与处理顺序无关。

若 $E_w'$ 中有边形成环，设按照某顺序处理时，某条边 $(u,v,w)$ 因形成环未被选中（即 $u,v$ 已连通），此时必存在一条由已加入的 $E_w'$ 中的边构成连接 $u$ 和 $v$ 的路径 $P$。若将 $(u,v,w)$ 替换为 $P$ 中任意边 $(u',v',w') \in P \cap E_w'$，此时 $H$ 仍为最大生成森林，且 $\mathcal{C}$ 中合并后的连通分量结构保持不变。因此，在不同的处理顺序下，虽然从 $E_w'$ 中选择的边可能不同，但均可通过该替换，最终的连通分量结构是唯一的。

因此处理完边权等于 $w$ 的边后，连通分量结构仍唯一确定。得证。

接下来，考虑只有一组询问的情况，判断这组边是否出现在同一棵最小生成树中。按照边权对边进行升序排序，并同时处理所有边权相同的边。在枚举到边权为 $w$ 的边时，确保已经按照 Kruskal 算法处理了原图中所有边权小于 $w$ 的边，然后依次处理边权为 $w$ 的边，并尝试将其加入图中。根据上述性质，处理顺序不重要，并且如果某条边无法加入，则说明该组边不会出现在同一棵最小生成树中。在处理完边权为 $w$ 的所有边后，需要从图中删除刚刚加入的询问的边，以免影响后续边的判断。

接着考虑如何处理多组询问。显然如果对每组询问单独处理，时间复杂度为 $O(\sum{k_i \log{k_i}} + m \sum{k_i})$。因此可以考虑离线处理，合并处理边权相同的边。具体而言，我们先对每组询问的边按边权分组，然后同时处理所有询问中边权相同的分组。与上面的方法类似，在处理边权为 $w$ 的边时，先确保已经按照 Kruskal 算法处理了原图中所有边权小于 $w$ 的边，然后依次处理同一批询问的边。在处理完成后，需要从图中删除刚刚加入的边，然后再处理下一组询问的边。

由于涉及删除最近加入的边，可以用可撤销并查集代替普通并查集，以实现线性删除。

AC 代码如下，时间复杂度为 $O(m (\log{n} + \log{m}) + W + \sum{k_i} \log{n})$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 5e5 + 5;

array<int, 3> e[N];
vector<array<int, 3>> g[N];
int fa[N], s[N], tp;
array<int, 2> stk[N];
bool ans[N];

int find(int x) {
    return fa[x] == x ? fa[x] : find(fa[x]);
}

bool merge(int x, int y) {
    x = find(x), y = find(y);
    if (x == y) return false;
    if (s[x] > s[y]) swap(x, y);
    s[y] += s[x];
    fa[x] = y;
    stk[++tp] = {x, y};
    return true;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, m, k;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> e[i][0] >> e[i][1] >> e[i][2];
    }
    cin >> k;
    for (int i = 0; i < k; i++) {
        int c;
        cin >> c;
        while (c--) {
            int x;
            cin >> x;
            g[e[x][2]].push_back({e[x][0], e[x][1], i});
        }
    }
    sort(e + 1, e + m + 1, [&](array<int, 3> &a, array<int, 3> &b) {
        return a[2] < b[2];
    });
    iota(fa + 1, fa + n + 1, 1);
    fill(s + 1, s + n + 1, 1);
    for (int i = 1, j = 1; i < N; i++) {
        while (j <= m && e[j][2] < i) {
            merge(e[j][0], e[j][1]);
            j++;
        }
        int l = 0;
        while (l < g[i].size()) {
            int r = l + 1, c = 0;
            while (r < g[i].size() && g[i][l][2] == g[i][r][2]) {
                r++;
            }
            while (l < r) {
                if (merge(g[i][l][0], g[i][l][1])) c++;
                else ans[g[i][l][2]] = true;
                l++;
            }
            while (c--) {
                auto p = stk[tp--];
                s[p[1]] -= s[p[0]];
                fa[p[0]] = p[0];
            }
        }
    }
    for (int i = 0; i < k; i++) {
        cout << (ans[i] ? "NO" : "YES") << '\n';
    }
    
    return 0;
}

参考资料

题解 CF891C 【Envy】 - 洛谷专栏：https://www.luogu.com.cn/article/ok5ea1ws

CF891C题解 - 洛谷专栏：https://www.luogu.com.cn/article/6uy5dohc

最小生成树相关性质 - cbdsopa - 博客园：https://www.cnblogs.com/cbdsopa/p/16035326.html

posted @ 2025-05-15 17:15 onlyblues 阅读(19) 评论(0) 收藏举报

刷新页面返回顶部

onlyblues

C. Envy

C. Envy

Input

Output

Example

Input

Output

Note

解题思路

参考资料

公告