奇素数回路

奇素数回路

题目描述

给定偶数 $n$，构造一个由 $1 \sim n$ 这 $n$ 个不同的整数构成环形数组 $a$，使得相邻两项的差均为奇素数。

奇素数是指除了 $2$ 以外的素数，最小的四个奇素数是 $3,5,7,11$。

输入描述:

每个测试文件均包含多组测试数据。第一行输入一个整数 $T\,(1 \leq T \leq 10^5)$ 代表数据组数，每组测试数据描述如下：

在一行上输入一个偶数 $n\,(2 \leq n \leq 10^5)$。

除此之外，保证单个测试文件的 $n$ 之和不超过 $2 \times 10^5$。

输出描述:

对于每一组测试数据，新起一行。如果不存在合法的环形数组，直接输出 $−1$。否则，输出 $n$ 个整数，表示构造的环形数组 $a$。

你需要保证数组 $a$ 是一个由 $1 \sim n$ 这 $n$ 个不同的整数组成的数组，下标从 $0$ 开始，满足任取 $0 \leq i < n$，$|a_i - a_{(i+1) \bmod n}|$ 均为奇素数。

示例1

输入

2
8
12

输出

1 4 7 2 5 8 3 6
1 6 11 4 9 12 7 2 5 10 3 8

说明

 

 

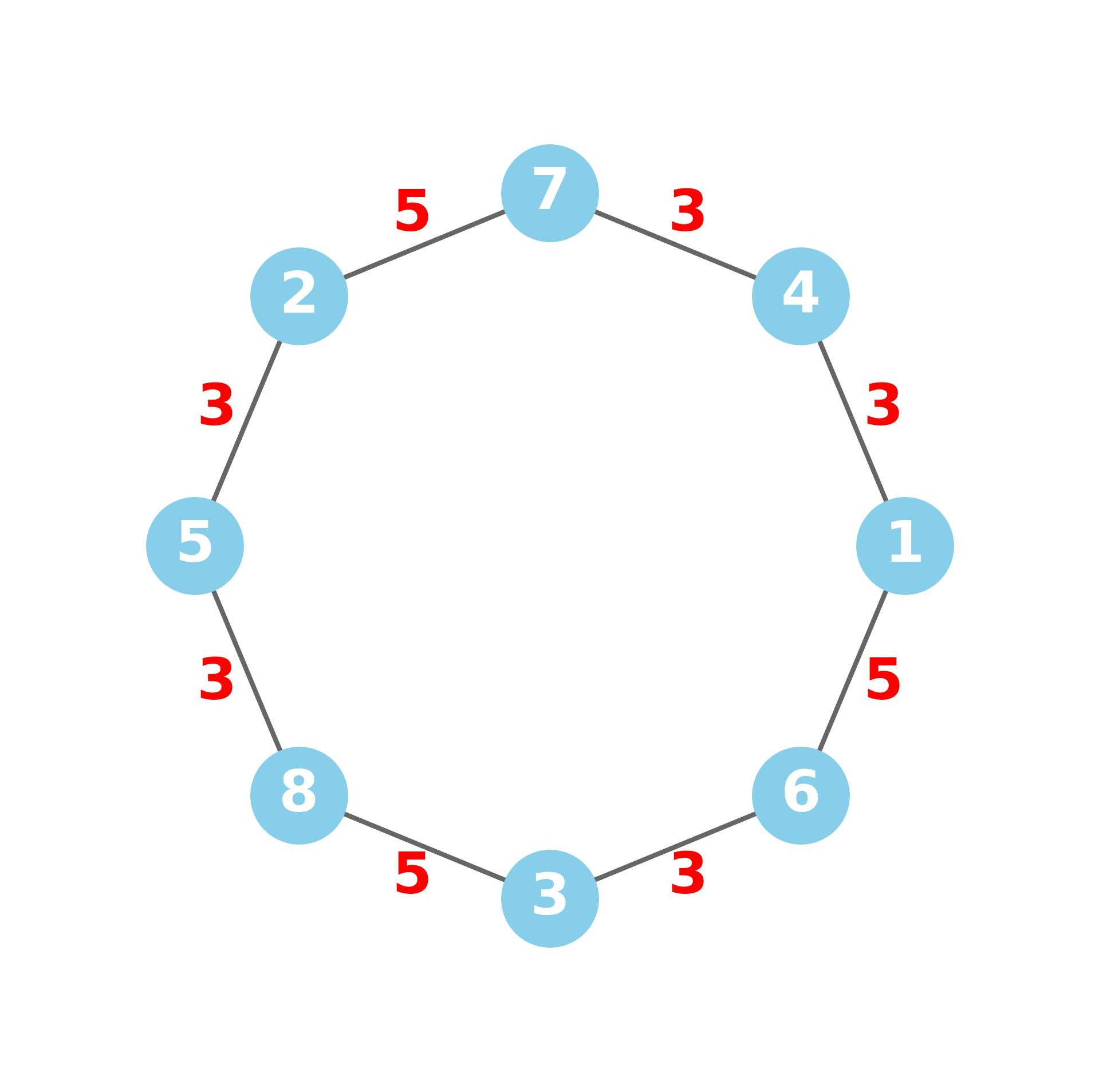
解题思路

  先说结论，如果 $n$ 可以拆成两个奇素数的和，则有解，否则无解。假设有奇素数 $p$ 和 $q$ 满足 $p+q = n$ 且 $p \ne q$，那么可以从 $1$ 开始通过 $+p$ 和 $-q$（或者 $+q$ 和 $-p$）来构造序列，只要在 $+p$ 或 $-q$ 后在 $1 \sim n$ 范围内且前面没有出现过，则可以构造出由 $1 \sim n$ 这 $n$ 个不同的整数且相邻两项的差均为奇素数的序列。

  比如有 $n = 8$，取 $p = 3$ 和 $q = 5$，构造的方式如下：${\color{Red}{1}}, \, 1\mathrm{+}3\mathrm{=}{\color{Red}{4}}, \, 4\mathrm{+}3\mathrm{=}{\color{Red}{7}}, \,7\mathrm{-}5\mathrm{=}{\color{Red}{2}}, \, 2\mathrm{+}3\mathrm{=}{\color{Red}{5}}, \, 5\mathrm{+}3\mathrm{=}{\color{Red}{8}}, \, 8\mathrm{-}5\mathrm{=}{\color{Red}{3}}, \, 3\mathrm{+}3\mathrm{=}{\color{Red}{6}}$。

  其实完全可以等价写成 $a_i = ((a_{i-1} + p - 1) \bmod n) + 1$ 的形式，因为如果 $a_{i-1} + p > n$ 此时 $a_i$ 应该选择 $a_{i-1} - q$，而 $((a_{i-1} + p - 1) \bmod n) + 1 = a_{i-1} + p - n = a_{i-1} - q$。进一步的，由于我们每次都 $+p$，实际上有 $a_{i} = ((i-1) \cdot p \bmod n) + 1$ $(1 \leq i \leq n)$。

  现在关键的问题是如何找到两个不同且和等于 $n$ 的奇素数。只需筛出 $1 \sim n$ 内的质数，然后依次枚举奇素数 $p$，如果 $p \ne n - p$ 且 $n - p$ 是奇素数，则有解。

  这样做为什么是正确的呢？首先容易知道如果由 $1 \sim n$ 构成相邻两项的差均为同一个奇素数的序列，这样的序列是不存在的，因为会存在重复元素。当存在相邻项的差至少有两种不同质数时，上述构造方法可以证明有解。然后再证明当 $a_{i} = ((i-1) \cdot p \bmod n) + 1$ $(1 \leq i \leq n)$ 可以构造出 $1 \sim n$ 的不同元素。

  先证明如果有奇素数 $p \ne q$ 且 $p+q=n$，有 $\gcd(p,n)=1$。反证法，如果 $\gcd(p,n) \ne 1$，由于 $p \leq n$，此时有 $\gcd(p,n)=p$。令 $n = kp$，有 $q = n - p = (k-1)p$，由于 $q$ 是奇素数，意味着只能 $k=2$，推出 $p = q$，矛盾。

  然后再证明当 $\gcd(p,n)=1$，$a_{i} = ((i-1) \cdot p \bmod n) + 1$ $(1 \leq i \leq n)$ 可以构造出 $1 \sim n$ 的不同元素。反证法，如果存在 $a_i = a_j$，即 $(i-1) \cdot p \bmod n = (j-1) \cdot p \bmod n \Rightarrow (i-j) \cdot p \equiv 0 \pmod{n} \Rightarrow n \mid (i-j) \cdot p$，由于 $\gcd(p,n)=1$，因此有 $n \mid i-j$。又因为 $|i-j|<n$，矛盾。

  AC 代码如下，时间复杂度为 $O(n)$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 2e5 + 5;

int prime[N], cnt;
bool vis[N];

void get_prime(int n) {
    cnt = 0;
    vis[1] = true;
    for (int i = 2; i <= n; i++) {
        if (!vis[i]) prime[cnt++] = i;
        for (int j = 0; prime[j] * i <= n; j++) {
            vis[prime[j] * i] = true;
            if (i % prime[j] == 0) break;
        }
    }
}

void solve() {
    int n;
    cin >> n;
    get_prime(n);
    for (int i = 1; i < cnt; i++) {
        int p = prime[i];
        if (!vis[n - p] && p != n - p) {
            for (int i = 0; i < n; i++) {
                cout << (1ll * i * p) % n + 1 << ' ';
            }
            cout << '\n';
            return;
        }
    }
    cout << -1 << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    
    return 0;
}

 

参考资料

  题解 | 题解E-G_牛客网：https://www.nowcoder.com/discuss/750468173170827264