[IOI 2008] Island

[IOI 2008] Island

题目描述

你准备浏览一个公园，该公园由 $N$ 个岛屿组成，当地管理部门从每个岛屿 $i$ 出发向另外一个岛屿建了一座长度为 $L_i$ 的桥，不过桥是可以双向行走的。同时，每对岛屿之间都有一艘专用的往来两岛之间的渡船。相对于乘船而言，你更喜欢步行。你希望经过的桥的总长度尽可能长，但受到以下的限制：

  • 可以自行挑选一个岛开始游览。
  • 任何一个岛都不能游览一次以上。
  • 无论任何时间，你都可以由当前所在的岛 $S$ 去另一个从未到过的岛 $D$。从 $S$ 到 $D$ 有如下方法：
    • 步行：仅当两个岛之间有一座桥时才有可能。对于这种情况，桥的长度会累加到你步行的总距离中。
    • 渡船：你可以选择这种方法，仅当没有任何桥和以前使用过的渡船的组合可以由 $S$ 走到 $D$ (当检查是否可到达时，你应该考虑所有的路径，包括经过你曾游览过的那些岛)。

注意，你不必游览所有的岛，也可能无法走完所有的桥。

请你编写一个程序，给定 $N$ 座桥以及它们的长度，按照上述的规则，计算你可以走过的桥的长度之和的最大值。

输入格式

第一行包含一个整数 $N$，即公园内岛屿的数目。

随后的 $N$ 行每一行用来表示一个岛。第 $i$ 行由两个以单空格分隔的整数，表示由岛 $i$ 筑的桥。第一个整数表示桥另一端的岛，第二个整数表示该桥的长度 $L_i$。你可以假设对于每座桥，其端点总是位于不同的岛上。

输出格式

仅包含一个整数，即可能的最大步行距离。

输入输出样例 #1

输入 #1

7
3 8
7 2
4 2
1 4
1 9
3 4
2 3

输出 #1

24

说明/提示

样例解释：

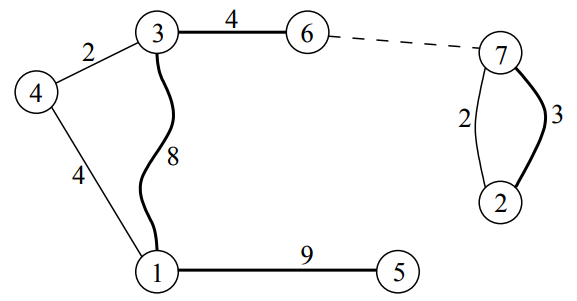
样例 $N=7$ 座桥，分别为 $(1-3), (2-7), (3-4), (4-1), (5-1), (6-3)$ 以及 $(7-2)$。注意连接岛 $2$ 与岛 $7$ 之间有两座不同的桥。

其中一个可以取得最大的步行距离的方法如下：

  • 由岛 $5$ 开始。
  • 步行长度为 $9$ 的桥到岛 $1$。
  • 步行长度为 $8$ 的桥到岛 $3$。
  • 步行长度为 $4$ 的桥到岛 $6$。
  • 搭渡船由岛 $6$ 到岛 $7$。
  • 步行长度为 $3$ 的桥到岛 $2$。

最后，你到达岛 $2$，而你的总步行距离为 $9+8+4+3=24$。

只有岛 $4$ 没有去。注意，上述游览结束时，你不能再游览这个岛。更准确地说：

  • 你不可以步行去游览，因为没有桥连接岛 $2$ (你现在的岛) 与岛 $4$。
  • 你不可以搭渡船去游览，因为你可由当前所在的岛 $2$ 到达岛 $4$。一个方法是：走 $(2-7)$ 桥，再搭你曾搭过的渡船由岛 $7$ 去岛 $6$，然后走 $(6-3)$ 桥，最后走 $(3-4)$ 桥。

数据范围：

对于 $100\%$ 的数据，$2\leqslant N\leqslant 10^6,1\leqslant L_i\leqslant 10^8$。

 

解题思路

  题目大意就是给定一个基环树森林（即有若干个相互独立的基环树），求每个基环树的最长路径的和。一个基环树的最长路径又称为基环树直径（类比树的直径），其中路径上的每个节点只能出现一次。

  基环树就是有一个环，环上的每个节点都挂着一棵树（可以为空）。基环树直径其实就是基环树上的一条简单路径，根据路径的两个端点，可以把所有路径分成两大类：

  1. 两个端点在同一棵树中。
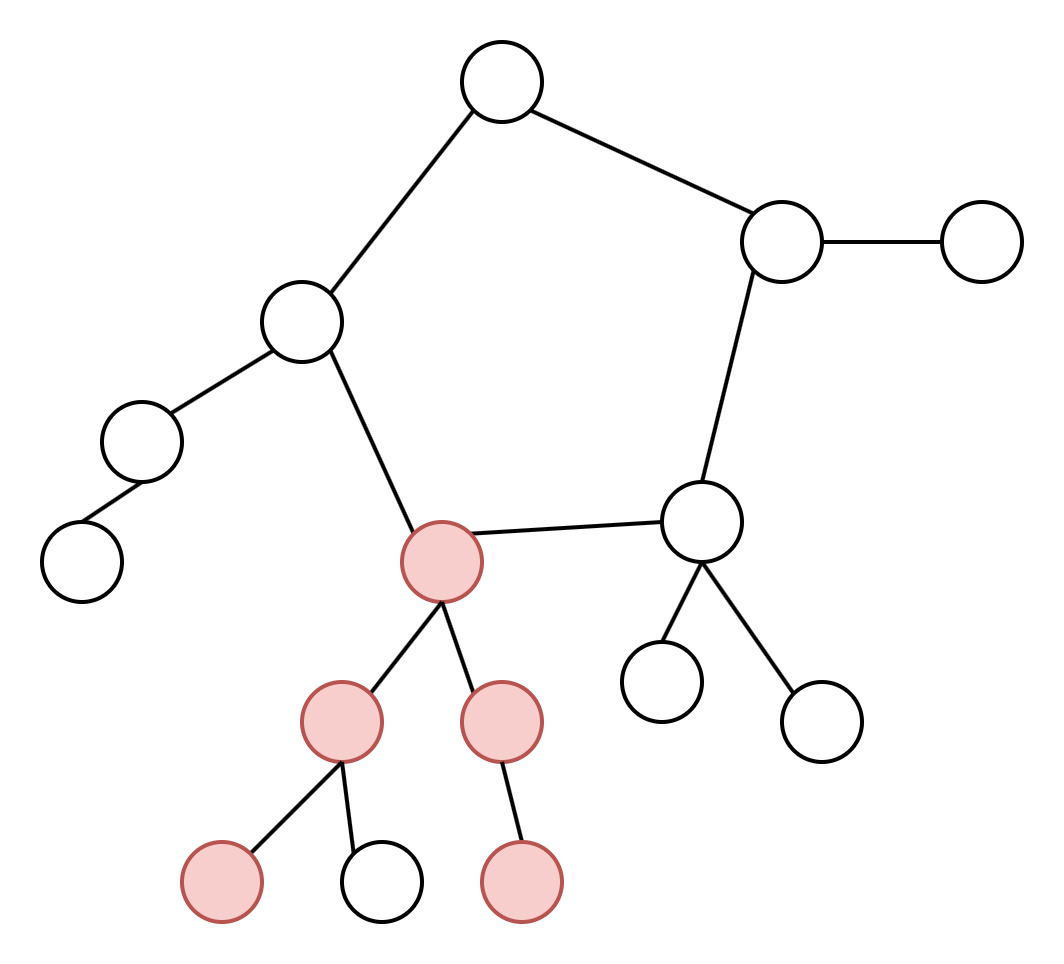
  2. 两个端点分别在不同的树中。

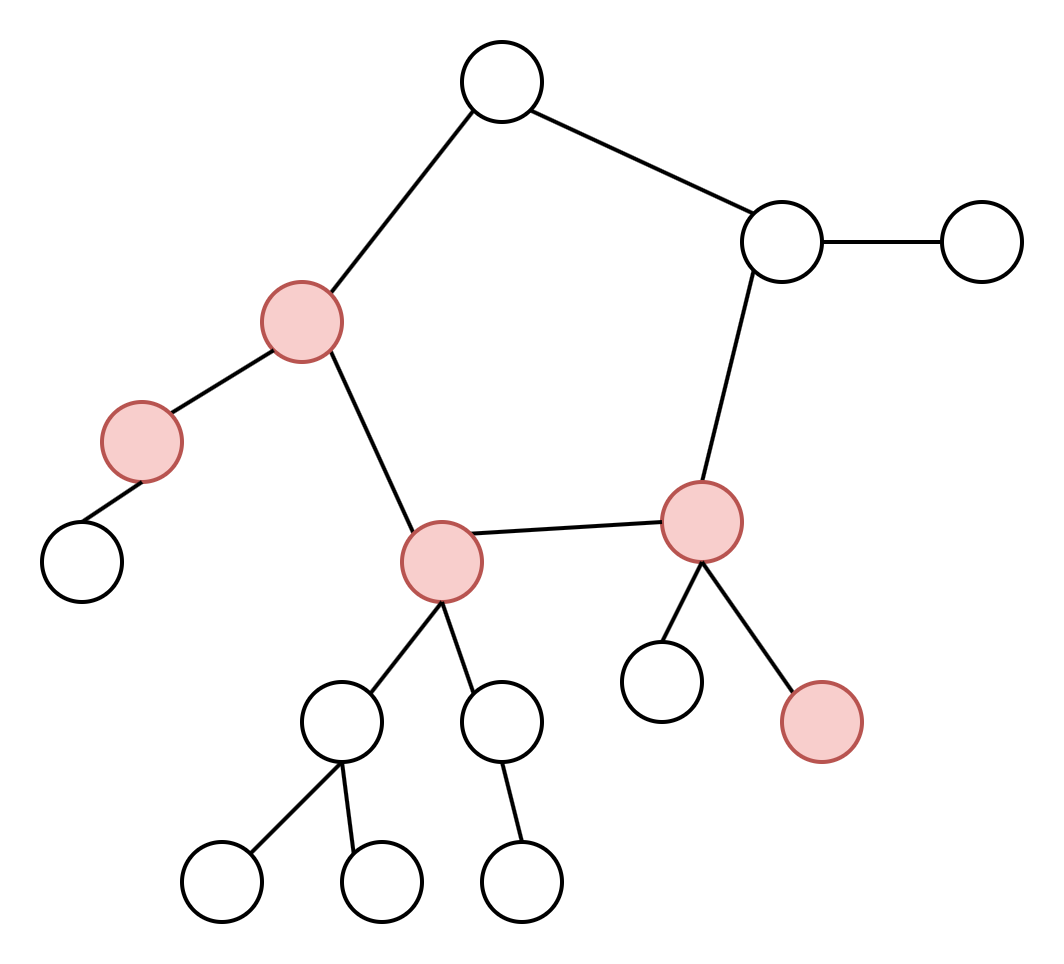
  其中第一种情况就是我们熟知的树的直径。为此，首先我们需要找到基环树的环，对于环上的每个节点，由于挂着一棵树，因此以环上的节点作为树根进行 dp 求树的直径。找环以及求树的直径在之后的部分详细描述。

  对于第二种情况，由于路径两个端点在不同的树中，因此往环的方向走会走到环上两个不同节点。因此为了求出第二种情况的最长路径，我们可以枚举环上两个不同的点 $u$ 和 $v$。由于其中一个端点在 $u$ 挂着的树中，我们可以选择树中距离 $u$ 最远的那点为端点，最远距离记作 $d_u$；同理选择 $v$ 挂着的树中距离 $v$ 最远的点为另外一个端点，最远距离记作 $d_v$。假设在环上 $u$ 和 $v$ 的最远距离为 $\text{dist}(u,v)$，那么 $d_u + d_v + \text{dist}(u,v)$ 就是经过环上 $u \to v$（或 $v \to u$）的所有路径的最长距离。

  显然我们不可能暴力枚举环上任意两点，考虑破环成链。假设顺时针遍历环上的点得到序列 $g$，把 $g$ 拷贝接到 $g$ 的后面（即 $g \gets \{g,g\}$），就是破环成链。假设环的大小为 $\text{sz}$（即环上有 $\text{sz}$ 个节点），枚举每个点 $u$，逆时针考虑另外一个点 $v \, (\{v \mid g_{u - \text{sz} + 1} \sim g_{u-1}\})$，使得 $d_u + d_v + \text{dist}(u,v)$ 有最大值。此时 $\text{dist}(u,v)$ 可以换成 $s_u - s_v$（因为一定会枚举到 $u$ 到 $v$ 最远距离的情况），其中 $s_u = \sum\limits_{i=1}^{u}{w_{g_{i-1},g_{i}}}$，$w_{u,v}$ 表示边 $(u,v)$ 的权值。

  式子可以改写成 $d_u + s_u + d_v - s_v$ 的形式，当我们枚举到 $u$ 时，为了得到 $\{v \mid g_{u - \text{sz} + 1} \sim g_{u-1}\}$ 中关于 $d_v -s_v$ 的最大值，只需用单调队列去维护大小为 $\text{sz}-1$ 的窗口内关于 $d_v -s_v$ 最大值的点即可。

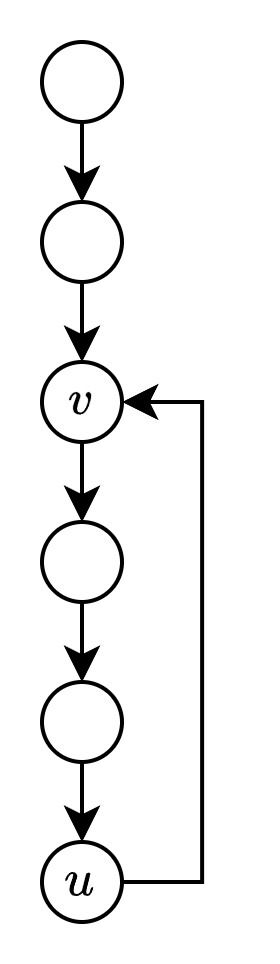
  下面讲如何找到基环树上的环。从基环树上任意一点开始 dfs，并记录递归的栈中有哪些点。当枚举到 $u$，然后其邻接点 $v$ 在栈内，如下图的情况，说明我们找到了环。当然在 dfs 的时候我们记录每个节点在搜索树中对应的父节点，这样我们就可以从 $u$ 开始，不断往父节点走直到 $v$，来找到环上所有点。具体实现参考 AC 代码中的函数 dfs1。

  然后是求树的直径。在找到环上的点后，对于环上的每一个点以这个点为树根，求挂在这个点的树的直径。由于树已经定根了，我们可以把树中所有路径根据路径的最高点进行分类。定义 $d_1[u]$ 表示从 $u$ 往下走的最远距离，$d_2[u]$ 表示从 $u$ 往下走的次远距离，那么 $d_1[u] + d_2[u]$ 就是以 $u$ 为最高点的路径的最长距离。更新方式为

$$\text{for } v \in \text{son}(u), \begin{cases}
(d_1[u],d_2[u]) = (d_1[v] + w_{u,v}, d_1[u]) &\text{if  } d_1[v] + w_{u,v} \geq d_1[u] \\
d_2[u] = d_1[v] + w_{u,v} &\text{if } d_1[v] + w_{u,v} > d_2[u]
\end{cases}$$

  最后树的直径就是 $\max\limits_{u}\{d_1[u]+d_2[u]\}$。另外上面第二种情况中的 $d_u$ 其实就是 $d_1[u]$。

  剩下的细节参考代码。

  AC 代码如下，时间复杂度为 $O(n)$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 1e6 + 5, M = N * 2;

int h[N], e[M], wt[M], ne[M], idx;
int fa[N], fw[N], g[M], sz;
bool vis[N], ins[N];
LL s[N], d1[N], d2[N], mx;
int q[N];

void add(int u, int v, int w) {
    e[idx] = v, wt[idx] = w, ne[idx] = h[u], h[u] = idx++;
}

void dfs1(int u, int p) {
    vis[u] = ins[u] = true; // vis[u] 用来记录 u 是否被访问过，ins[u] 用来表示 u 是否在递归栈中
    for (int i = h[u]; i != -1; i = ne[i]) {
        if ((i ^ 1) == p) continue;
        int v = e[i];
        if (!vis[v]) {
            fa[v] = u, fw[v] = wt[i];   // fa[v] 表示 v 在搜索树中的父节点，fw[v] 表示 v 到父节点的边权
            dfs1(v, i);
        }
        else if (ins[v]) {  // 找到环
            fa[v] = u, fw[v] = wt[i];
            for (int i = u; ; i = fa[i]) {
                g[sz++] = i;
                if (i == v) break;
            }
        }
    }
    ins[u] = false;
}

void dfs2(int u, int p) {
    d1[u] = d2[u] = 0;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int v = e[i];
        if (v == p || ins[v]) continue; // 避免搜到环上的点
        dfs2(v, u);
        LL w = d1[v] + wt[i];
        if (w >= d1[u]) d2[u] = d1[u], d1[u] = w;
        else if (w > d2[u]) d2[u] = w;
    }
    mx = max(mx, d1[u] + d2[u]);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    memset(h, -1, sizeof(h));
    for (int i = 1; i <= n; i++) {
        int x, y;
        cin >> x >> y;
        add(i, x, y), add(x, i, y);
    }
    LL ret = 0;
    for (int i = 1; i <= n; i++) {
        if (vis[i]) continue;
        sz = mx = 0;
        dfs1(i, -1);
        memmove(g + sz, g, sz << 2);
        for (int i = 1; i < sz << 1; i++) {
            s[i] = s[i - 1] + fw[g[i - 1]];
            ins[g[i]] = true;   // 标记环上的点，在求树的直径是避免访问到环上的点
        }
        for (int i = 0; i < sz; i++) {
            dfs2(g[i], 0);
        }
        int hh = 0, tt = -1;
        LL t = mx;
        for (int i = 0; i < sz << 1; i++) {
            if (q[hh] <= i - sz) hh++;
            if (hh <= tt) t = max(t, d1[g[i]] + s[i] + d1[g[q[hh]]] - s[q[hh]]);
            while (hh <= tt && d1[g[q[tt]]] - s[q[tt]] < d1[g[i]] - s[i]) {
                tt--;
            }
            q[++tt] = i;
        }
        ret += t;
    }
    cout << ret;
    
    return 0;
}

 

参考资料

  AcWing 358. 岛屿：https://www.acwing.com/activity/content/code/content/612104/

  P4381 [IOI2008]Island：https://www.luogu.com.cn/article/t3ufkiek

posted @ 2025-04-16 21:45  onlyblues  阅读(18)  评论(0)    收藏  举报
Web Analytics