红黑树--RB_tree
- 红黑树演示网站https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
- 平衡树是指树的左右子树高度差不超过一,而红黑树是对黑色节点完全平衡的二叉搜索树。
- 红黑树是从2-3-4 树变化而来,与AVL相比较平衡没有那么严格。
- 红黑树在C++中是实现set/multiset、map/multimap的底层容器。
- 红黑树满足如下要求
- 1.每个节点不是红色就是黑色
- 2.根节点为黑色
- 3.如果节点为红色,其子节点必为黑色
- 4.任意节点至NULL节点(树尾端)的任何路径,所含黑色节点相同
- 根据规则4可知,新增节点必须为红
- 根据规则3可知,新增节点父节点必须为黑
A. 2-3-4 树

- 2-3-4树的介绍可参照heyanxi0101·234树
- 由于红黑树是由2-3-4树来的,所以有以下转换关系。(红色与黑色结合,可恢复2-3-4树。但不能连着的两个黑色结合)

- 二节点对应红黑树的一个红色节点(当该节点为根时,为黑色节点)。
- 三节点对应的必是上黑下红。
- 四节点转换后对应如图。
- 当新增一个节点时,对应关系如下图

- 需要注意的是三节点的操作,需要调整到图示最终的对应结果。
- 当伯父节点为黑色时,该节点不是与祖父一起的,其实还是三节点。
- 三节点只需一次(外则插入)或者两次(内侧插入)左右旋即可。
- 当四节点调整完后,若祖祖父还是红色,即两个红色挨着,需要继续向上调整,直到不再有连续红色。
B. 红黑树的插入
- 根据上述图的描述,可以得到如下对树的平衡规则。父节点为当前(未平衡前的)插入节点的父节点。插入的节点为红色。
- 当父节点为黑色时,不调整树。即上图中新增一个节点到二节点情况。
- 当父节点为红色时,伯父节点不存在(或为黑色),需要左旋与右旋操作,调整成上图新增一个节点到三节点的最终结果。
- 当父节点为红色时,伯父节点为红色,只需交换颜色即可。如上图新增一个节点到四节点所示。
- 若祖父为根节点,则变为黑色。
- 但当祖父与祖祖父都为红色时,需要再次向上处理,直到不再有父子连续为红的情况。
B1. 树的左右旋
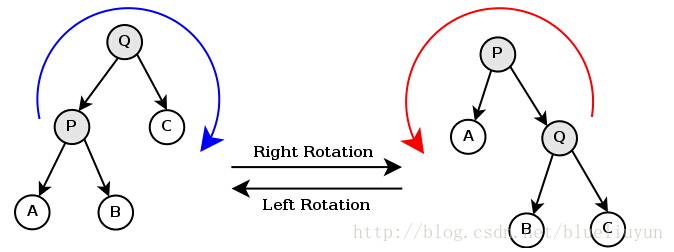
rightRatote、leftRatote
/* root root
parent node
/ \ / \
node brother ---> left parent
/ \ / \
left right right brother
*/
template <typename value>
void rb_tree<value>::rightRatote(pointer node)
{
if (!node || !parent(node)) //空节点或没有父节点
return;
pointer root = parent(parent(node)); //祖父节点
left(parent(node)) = right(node);
if (right(node) != nullptr)
right(node)->parent = parent(node);
parent(parent(node)) = node;
right(node) = parent(node);
parent(node) = root;
if (!root)//若root为空,即parent是根节点
header = node;
else if (value(node) <= value(root))//判断时否是root的左节点
left(root) = node;
else
right(root) = node;
}
/* root root
node parent
/ \ / \
parent right <--- brother node
/ \ / \
brother left left right
*/
template <typename Value>
void rb_tree<Value>::leftRatote(pointer node)
{
if (!node || !parent(node)) //空节点或没有父节点
return;
pointer root = parent(parent(node));
right(parent(node)) = left(node);
if (left(node) != nullptr)
left(node)->parent = parent(node);
parent(parent(node)) = node;
left(node) = parent(node);
parent(node) = root;
if (!root)//若root为空,即parent是根节点
header = node;
else if (value(node) <= value(root))
left(root) = node;
else
right(root) = node;
}
B2. 二叉树搜索树的插入
- 需要先将新节点插入到指定位置,再进行平衡。此处代码是不可插入重复值。
insert_unique
template <typename Value>
bool rb_tree<Value>::insert_unique(value_type v)
{
pointer ptr = new node_type; //创建一个节点
value(ptr) = v; //初始化该值
left(ptr) = nullptr;
right(ptr) = nullptr;
parent(ptr) = nullptr;
ptr->color = red_node; //新增节点为红节点
if (!header) //若树为空 header为保存的根节点
{
header = ptr;
header->color = black_node; //根节点颜色为黑色
return true;
}
pointer cur = header, temp = nullptr;
//找到待插入节点的父节点
while (cur != nullptr)
{
temp = cur;
if (v < value(cur))
cur = left(cur);
else
cur = right(cur);
}
//temp此时即为待插入节点的父节点
//与祖父节点值相同则不插入 或者 与父节点相同
if ((parent(temp) && value(parent(temp)) == v)||value(temp) == v)
{
delete ptr;
return false;
}
parent(ptr) = temp;
if (value(temp) > v)
left(temp) = ptr;
else if (value(temp) < v)
right(temp) = ptr;
balance_tree(ptr); // 插入完成后再调整树的平衡
count++;
return true;
}
B3. 红黑树平衡的调整
balance_tree
template <typename Value>
void rb_tree<Value>::balance_tree(pointer ptr)
{
pointer PP = parent(parent(ptr)); //祖父节点
if (!PP) //若没有祖父节点,说明父节点为根节点,则直接返回
return;
if (parent(ptr)->color == red_node)
{
//伯父节点存在 且都为红色
if (PP->left != nullptr && PP->right != nullptr && PP->left->color == red_node && PP->right->color == red_node)
{
//即插入四节点情况,只需更改颜色即可
PP->color = red_node;
PP->left->color = black_node;
PP->right->color = black_node;
//若PP为根节点
if (header == PP)
PP->color = black_node;
//祖父与祖祖父都为红色 继续调整
else if (parent(PP) != nullptr && parent(PP)->color == red_node)
balance_tree2(PP);
}
//伯父节点不存在 或者为黑色时
//左右外侧插入时,只需要左右旋一次即可 注意颜色要更改
else if ((left(parent(ptr)) == ptr && PP->left == parent(ptr)) || (right(parent(ptr)) == ptr && PP->right == parent(ptr)))
{
PP->color = red_node;
parent(ptr)->color = black_node;
if (left(parent(ptr)) == ptr)
rightRatote(parent(ptr));
else
leftRatote(parent(ptr));
}
//内侧插入 需要旋转两次。 第一次旋转完后就成上面的外侧插入了
else
{
ptr->color = black_node;
PP->color = red_node;
if (left(parent(ptr)) == ptr)
{
rightRatote(ptr);
leftRatote(ptr);
}
else
{
leftRatote(ptr);
rightRatote(ptr);
}
}
}
}
C. 红黑树节点的删除

- 对于节点值的删除,一般是找到前驱节点或后继节点,交换其值,再删除前驱节点或后继节点。最后再平衡该树。
- 对于平衡树来说,前驱节点或后继节点必定是叶子节点或叶子节点的父节点,在倒数一二层,且最多只有一个孩子。
- 一般删除有如下情况
- 当删除节点为3,4节点时可以通过内部自行解决。
- 当删除节点为2节点时,需要父节点和兄弟节点来解决。
- 红黑树节点删除规则如下
- 找到待删除值的前驱或后继节点,交换值,再删除前驱或后继节点T。
- 当T为红色时(三四节点情况存在,且必然没有孩子),则直接删除。因为直接删除不影响黑色平衡。
- 若红色前驱或后继节点T有孩子,则该左右子树不可能平衡。
- 当T为黑色无孩子(二节点情况)时,需要调整父节点与兄弟节点。
- 兄弟节点是红色,父节点变红,兄弟节点变黑,再对父节点左旋或右旋。此时T的兄弟节点变为黑色节点了。
- 若兄弟节点黑色有一个孩子(三节点情况),则父节点到T的位置,兄弟节点需要左旋右旋出一个最小值节点作为父节点。
- 若兄弟节点黑色有两个孩子,仍然可以父节点到T的位置,兄弟节点出一个最小值节点作为父节点(需要一次右旋,一次左旋)。
- 若兄弟节点孩子,则在兄弟节点变红基础上。
- 若父节点为红色,父亲变为黑色即可。
- 若父节点为黑色,则将叔父变成红色。若祖祖父也为黑色需要往上递归改变,直到当前节点为红色或者根节点
- 当T为黑色有一个孩子(三节点情况)时,孩子颜色设置为黑色,与孩子交换位置后删除即可。父亡子替
C1. 寻找前驱节点
- 树节点的删除一般是找其前驱节点或者后继节点的来替代,删除的实际上是该前驱节点或者后继节点的内存。
- 此处用前驱节点来替代,代码如下。
predecessor
// 返回值的typename可以指定后面的这个名字是类中的类型成员,而不是数据成员
template <typename Value>
typename rb_tree<Value>::pointer rb_tree<Value>::predecessor(pointer cur)
{
// 返回前驱节点
if (left(cur) == nullptr)
return nullptr;
cur = left(cur);
while (right(cur) != nullptr)
{
cur = right(cur);
}
return cur;
}
C2. 红黑树节点的删除
- 先找到要删除的节点,再找到其前驱节点(后继节点也可以),用该节点的值覆盖给要删除的节点。最后删除前驱节点内存即可。
findByValue,deleteValue
template <typename Value>
typename rb_tree<Value>::pointer rb_tree<Value>::findByValue(value_type v)
{
pointer cur = header;
while (cur != nullptr)
{
if (value(cur) < v)
cur = right(cur);
else if (value(cur) > v)
cur = left(cur);
else
break;
}
return cur;
}
//可自行优化该部分代码
template <typename Value>
bool rb_tree<Value>::deleteValue(value_type v)
{
pointer cur = findByValue(v);
if (!cur)
return false;
// 需要被删除的前驱节点
pointer del = predecessor(cur);
if (!del) //没有前驱节点,删除自身
del = cur;
else
cur->value_filed = del->value_filed;
pointer deal = del;
// 红色直接删除,其必然没有孩子,否则左右子树不可能平衡
if (del->color == red_node)
{
if (left(parent(del)) == del)
left(parent(del)) = nullptr;
else
right(parent(del)) = nullptr;
delete del;
count--;
return true;
}
while (deal != nullptr && deal != header && deal->color == black_node)
{
if (!left(deal) && !right(deal)) //黑色无孩子节点
{
// 若兄弟节点是红色,让父节点变红,兄弟节点变黑,再对父节点左旋或右旋,使兄弟节点为黑色
if (right(parent(deal))->color == red_node || left(parent(deal))->color == red_node)
{
parent(deal)->color = red_node;
if (right(parent(deal)) != deal)
{
right(parent(deal))->color = black_node;
leftRatote(right(parent(deal)));
}
else
{
left(parent(deal))->color = black_node;
leftRatote(left(parent(deal)));
}
break;
}
pointer bro = right(parent(deal)) == deal ? left(parent(deal)) : right(parent(deal));
// 黑色兄弟节点有两个孩子 直接左旋或右旋一次
if (left(bro) != nullptr && right(bro) != nullptr)
{
parent(deal)->color = black_node;
if (parent(deal)->left == bro)
{
parent(deal)->right = nullptr;
rightRatote(bro);
}
else
{
parent(deal)->left = nullptr;
leftRatote(bro);
}
break;
}
// 黑色兄弟节点无孩子节点
else if (left(bro) == nullptr && right(bro) == nullptr)
{
bro->color = red_node;
if (parent(deal)->color == red_node)
{
parent(deal)->color = black_node;
if (parent(deal)->left == bro)
right(parent(deal)) = nullptr;
else
left(parent(deal)) = nullptr;
break;
}
else
{
if (parent(bro)->right == deal)
parent(deal)->right = nullptr;
else
parent(deal)->left = nullptr;
// 递归往上
deal = parent(bro);
}
}
// 黑色兄弟节点有一个孩子节点
else
{
if (left(bro) != nullptr && parent(bro)->right == bro)
{
rightRatote(left(bro));
bro = parent(bro);
}
else if (right(bro) != nullptr && parent(bro)->left == bro)
{
leftRatote(right(bro));
bro = parent(bro);
}
if (parent(bro)->right == bro)
{
leftRatote(bro);
parent(deal)->left = nullptr;
}
else
{
rightRatote(bro);
parent(deal)->right = nullptr;
}
break;
}
}
else
{ //黑色一个孩子,直接换位置后删除即可
if (left(deal) == nullptr)
leftRatote(deal->right);
else
rightRatote(deal->left);
parent(deal)->color = black_node;
left(parent(deal)) = nullptr;
right(parent(deal)) = nullptr;
break;
}
}
delete del;
count--;
return true;
}
完整代码
rb_tree.cpp
#include <iostream>
#include <new>
typedef bool clolor_type;
const clolor_type red_node = false; //红色为0
const clolor_type black_node = true; //黑色为1
//节点结构
template <typename Value>
struct tree_node
{
typedef tree_node<Value> *link_type;
clolor_type color;
link_type parent;
link_type left;
link_type right;
Value value_filed;
};
template <typename Value>
class rb_tree
{
private:
typedef tree_node<Value> node_type;
typedef tree_node<Value> *pointer;
typedef Value value_type;
inline pointer &left(pointer node) { return (pointer &)node->left; }
inline pointer &right(pointer node) { return (pointer &)node->right; }
inline pointer &parent(pointer node) { return (pointer &)node->parent; }
inline value_type &value(pointer node) { return (value_type &)node->value_filed; }
void balance_tree(pointer ptr);
void leftRatote(pointer node);
void rightRatote(pointer node);
void freeMemory(pointer cur); //释放cur为根节点的树
pointer predecessor(pointer cur);
pointer findByValue(value_type v);
public:
pointer header;
int count = 0;
rb_tree() : header(nullptr){};
~rb_tree();
bool insert_unique(value_type v);
bool deleteValue(value_type v);
void display();
void display2();
};
// 返回值的typename可以指定后面的这个名字是类中的类型成员,而不是数据成员
template <typename Value>
typename rb_tree<Value>::pointer rb_tree<Value>::predecessor(pointer cur)
{
// 返回前驱节点
if (left(cur) == nullptr)
return nullptr;
cur = left(cur);
while (right(cur) != nullptr)
{
cur = right(cur);
}
return cur;
}
template <typename Value>
typename rb_tree<Value>::pointer rb_tree<Value>::findByValue(value_type v)
{
pointer cur = header;
while (cur != nullptr)
{
if (value(cur) < v)
cur = right(cur);
else if (value(cur) > v)
cur = left(cur);
else
break;
}
return cur;
}
template <typename Value>
bool rb_tree<Value>::deleteValue(value_type v)
{
pointer cur = findByValue(v);
if (!cur)
return false;
// 需要被删除的前驱节点
pointer del = predecessor(cur);
if (!del) //没有前驱节点,删除自身
del = cur;
else
cur->value_filed = del->value_filed;
pointer deal = del;
// 红色直接删除,其必然没有孩子,否则左右子树不可能平衡
if (del->color == red_node)
{
if (left(parent(del)) == del)
left(parent(del)) = nullptr;
else
right(parent(del)) = nullptr;
delete del;
count--;
return true;
}
while (deal != nullptr && deal != header && deal->color == black_node)
{
if (!left(deal) && !right(deal)) //黑色无孩子节点
{
// 若兄弟节点是红色,让父节点变红,兄弟节点变黑,再对父节点左旋或右旋,使兄弟节点为黑色
if (right(parent(deal))->color == red_node || left(parent(deal))->color == red_node)
{
parent(deal)->color = red_node;
if (right(parent(deal)) != deal)
{
right(parent(deal))->color = black_node;
leftRatote(right(parent(deal)));
}
else
{
left(parent(deal))->color = black_node;
leftRatote(left(parent(deal)));
}
break;
}
pointer bro = right(parent(deal)) == deal ? left(parent(deal)) : right(parent(deal));
// 黑色兄弟节点有两个孩子 直接左旋或右旋一次
if (left(bro) != nullptr && right(bro) != nullptr)
{
parent(deal)->color = black_node;
if (parent(deal)->left == bro)
{
parent(deal)->right = nullptr;
rightRatote(bro);
}
else
{
parent(deal)->left = nullptr;
leftRatote(bro);
}
break;
}
// 黑色兄弟节点无孩子节点
else if (left(bro) == nullptr && right(bro) == nullptr)
{
bro->color = red_node;
if (parent(deal)->color == red_node)
{
parent(deal)->color = black_node;
if (parent(deal)->left == bro)
right(parent(deal)) = nullptr;
else
left(parent(deal)) = nullptr;
break;
}
else
{
if (parent(bro)->right == deal)
parent(deal)->right = nullptr;
else
parent(deal)->left = nullptr;
// 递归往上
deal = parent(bro);
}
}
// 黑色兄弟节点有一个孩子节点
else
{
if (left(bro) != nullptr && parent(bro)->right == bro)
{
rightRatote(left(bro));
bro = parent(bro);
}
else if (right(bro) != nullptr && parent(bro)->left == bro)
{
leftRatote(right(bro));
bro = parent(bro);
}
if (parent(bro)->right == bro)
{
leftRatote(bro);
parent(deal)->left = nullptr;
}
else
{
rightRatote(bro);
parent(deal)->right = nullptr;
}
break;
}
}
else
{ //黑色一个孩子,直接换位置后删除即可
if (left(deal) == nullptr)
leftRatote(deal->right);
else
rightRatote(deal->left);
parent(deal)->color = black_node;
left(parent(deal)) = nullptr;
right(parent(deal)) = nullptr;
break;
}
}
delete del;
count--;
return true;
}
template <typename Value>
rb_tree<Value>::~rb_tree()
{
freeMemory(header);
}
template <typename Value>
void rb_tree<Value>::freeMemory(pointer cur)
{
if (!cur)
return;
//释放cur为根节点的树
pointer left = cur->left, right = cur->right;
delete cur;
if (left)
freeMemory(left);
if (right)
freeMemory(right);
}
/* root root
parent node
/ \ / \
node brother ---> left parent
/ \ / \
left right right brother
*/
template <typename value>
void rb_tree<value>::rightRatote(pointer node)
{
if (!node || !parent(node)) //空节点或没有父节点
return;
pointer root = parent(parent(node)); //祖父节点
left(parent(node)) = right(node);
if (right(node) != nullptr)
right(node)->parent = parent(node);
parent(parent(node)) = node;
right(node) = parent(node);
parent(node) = root;
if (!root) //若root为空,即parent是根节点
header = node;
else if (value(node) <= value(root)) //判断时否是root的左节点
left(root) = node;
else
right(root) = node;
}
/* root root
node parent
/ \ / \
parent right <--- brother node
/ \ / \
brother left left right
*/
template <typename Value>
void rb_tree<Value>::leftRatote(pointer node)
{
// 注意被旋转的node节点会跑到上面去
if (!node || !parent(node)) //空节点或没有父节点
return;
pointer root = parent(parent(node));
right(parent(node)) = left(node);
if (left(node) != nullptr)
left(node)->parent = parent(node);
parent(parent(node)) = node;
left(node) = parent(node);
parent(node) = root;
if (!root) //若root为空,即parent是根节点
header = node;
else if (value(node) <= value(root))
left(root) = node;
else
right(root) = node;
}
//无重复插入
template <typename Value>
bool rb_tree<Value>::insert_unique(value_type v)
{
pointer ptr = new node_type; //创建一个节点
value(ptr) = v; //初始化该值
left(ptr) = nullptr;
right(ptr) = nullptr;
parent(ptr) = nullptr;
ptr->color = red_node; //新增节点为红节点
if (!header) //若树为空 header为保存的根节点
{
header = ptr;
header->color = black_node; //根节点颜色为黑色
return true;
}
pointer cur = header, temp = nullptr;
//找到待插入节点的父节点
while (cur != nullptr)
{
temp = cur;
if (v < value(cur))
cur = left(cur);
else
cur = right(cur);
}
// temp此时即为待插入节点的父节点
//与祖父节点值相同则不插入 或者 与父节点相同
if ((parent(temp) && value(parent(temp)) == v) || value(temp) == v)
{
delete ptr;
return false;
}
parent(ptr) = temp;
if (value(temp) > v)
left(temp) = ptr;
else if (value(temp) < v)
right(temp) = ptr;
balance_tree(ptr); // 插入完成后再调整树的平衡
count++;
return true;
}
template <typename Value>
void rb_tree<Value>::balance_tree(pointer ptr)
{
pointer PP = parent(parent(ptr)); //祖父节点
if (!PP) //若没有祖父节点,说明父节点为根节点,则直接返回
return;
if (parent(ptr)->color == red_node)
{
//伯父节点存在 且都为红色
if (PP->left != nullptr && PP->right != nullptr && PP->left->color == red_node && PP->right->color == red_node)
{
//即插入四节点情况,只需更改颜色即可
PP->color = red_node;
PP->left->color = black_node;
PP->right->color = black_node;
//若PP为根节点
if (header == PP)
PP->color = black_node;
//祖父与祖祖父都为红色 继续调整
else if (parent(PP) != nullptr && parent(PP)->color == red_node)
balance_tree(PP);
}
//伯父节点不存在 或者为黑色时
//左右外侧插入时,只需要左右旋一次即可 注意颜色要更改
else if ((left(parent(ptr)) == ptr && PP->left == parent(ptr)) || (right(parent(ptr)) == ptr && PP->right == parent(ptr)))
{
PP->color = red_node;
parent(ptr)->color = black_node;
if (left(parent(ptr)) == ptr)
rightRatote(parent(ptr));
else
leftRatote(parent(ptr));
}
//内侧插入 需要旋转两次。 第一次旋转完后就成上面的外侧插入了
else
{
ptr->color = black_node;
PP->color = red_node;
if (left(parent(ptr)) == ptr)
{
rightRatote(ptr);
leftRatote(ptr);
}
else
{
leftRatote(ptr);
rightRatote(ptr);
}
}
}
}
template <typename Value>
void rb_tree<Value>::display() //用循环进行中序遍历 用递归更方便
{
if (header == nullptr)
return;
pointer cur = header;
while (cur->left != nullptr) //第一位元素是最左侧元素
{
cur = cur->left;
}
while (cur != nullptr)
{
std::cout << cur->value_filed << "(" << cur->color << ") ";
if (cur->right != nullptr)
{ //有右节点就往右走
cur = right(cur);
while (cur->left != 0) //一直走左边到底
cur = cur->left;
}
else
{
pointer y = cur->parent;
//若本身是右节点(既大于该值),就一直上溯,直到不为右子节点为止
while (y != nullptr && cur == y->right)
{
cur = y;
y = y->parent;
}
cur = y;
}
}
std::cout << std::endl;
}
//用循环实现前序遍历 递归更方便
template <typename Value>
void rb_tree<Value>::display2()
{
if (!header)
return;
pointer cur = header;
while (cur != nullptr)
{
std::cout << cur->value_filed << "(" << cur->color << ") ";
if (cur->left != nullptr)
cur = cur->left;
else
{
if (cur->right != nullptr)
cur = cur->right;
else
{
pointer y = cur->parent;
if (!y)
return;
//直到兄弟节点不为空 或者 右侧不是自己
while ((cur == y->left && y->right == nullptr) || cur == y->right)
{
cur = y;
y = y->parent;
if (y == nullptr)
{
std::cout << std::endl;
return;
}
}
cur = y->right;
}
}
}
std::cout << std::endl;
}
int main()
{
using namespace std;
rb_tree<int> tree;
int num = 0;
for (int i = 1; i <= 8; i++)
tree.insert_unique(i);
tree.display2();
tree.deleteValue(6);
tree.deleteValue(7);
tree.display2();
return 0;
}
参考视频: https://www.bilibili.com/video/BV135411h7wJ







 浙公网安备 33010602011771号
浙公网安备 33010602011771号