状态空间表达式及其实现：现代控制原理基础

状态空间表达式

我们知道，传递函数是线性时不变（LTI）系统在零输入条件下，输出信号的拉氏变换与输入信号的拉氏变换之比，是对系统外部的描述（外部模型），体现了系统的封装特性，但是没有揭示系统内部细节。也即同一传递函数的系统有多种具体的实现方式。在现代控制理论中，状态空间方程被用以描述系统内部关系（内部模型），该模型不仅描述了输入-输出之间的行为，还在任何初始条件下都能揭示系统的内部行为。简单说，就是该模型也描述了一些中间变量，而这些中间变量足以表示系统内部的所有细节。
例如，对于如下图的RLC电路：

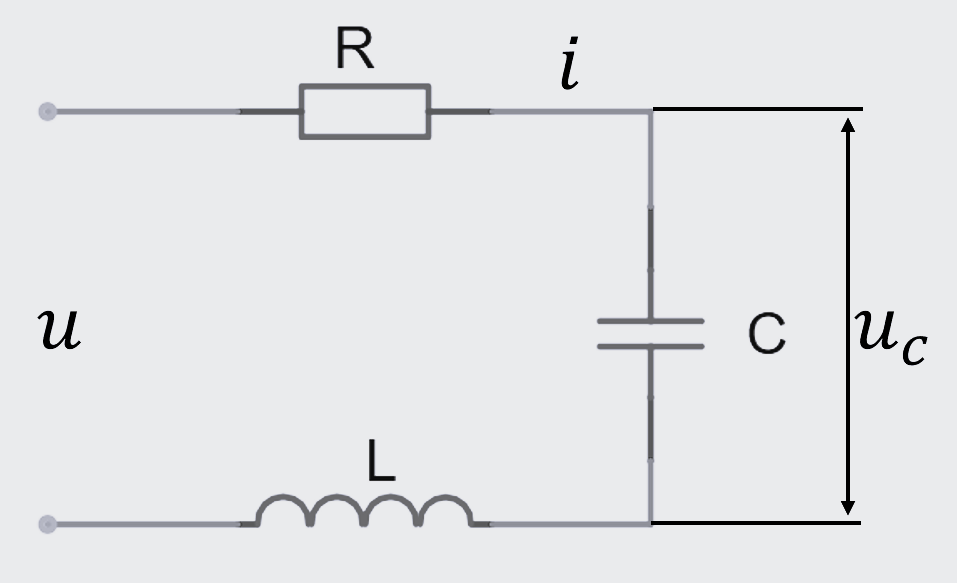
有：
$$\{\begin{array}{l}L\frac{di}{dt}+Ri+\frac{1}{C}\int idt=u\\ u_C=\frac{1}{C}\int idt\end{array}(对于u为输入,u_c为输出)$$
显然，通过求解方程组，可以得到表示输入输出关系的一个微分方程，经由拉氏变换则可以得到传递函数。
此时，若取$i$、$\int idt$两个不同阶的表达式作为中间变量，同时有$y=u_C$作为系统输出变量，分别对应：
$$\{\begin{array}{l}{x}_1=i\\ x_2=\int idt\\ y=u_C\end{array}$$
代入原方程组有：
$$\{\begin{array}{l}L\frac{d{x}_1}{dt}+R{x}_1+\frac{1}{C}{x}_2=u\\ y=\frac{1}{C}{x}_2\end{array}$$
把方程组拆成关于两个中间变量的一阶微分方程和一个输出方程，有：
$$\{\begin{array}{l}\frac{d{x}_1}{dt}=-\frac{R}{L}{x}_1-\frac{1}{LC}{x}_2+\frac{1}{L}u\\ \frac{d{x}_2}{dt}=x_1\\ y=\frac{1}{C}{x}_2\end{array}$$
这里令
$$\{\begin{array}{rl}{\dot{x}}_1& =\frac{d{x}_1}{dt}\\ {\dot{x}}_2& =\frac{d{x}_2}{dt}\end{array}$$
有：
$$\{\begin{array}{l}{\dot{x}}_1=-\frac{R}{L}{x}_1-\frac{1}{LC}{x}_2+\frac{1}{L}u\\ {\dot{x}}_2=x_1\\ y=\frac{1}{C}{x}_2\end{array}$$
使用矩阵表示有：
$$\{\begin{array}{l}\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}-\frac{R}{L}& -\frac{1}{LC}\\ 1& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]u\\ y=\left[\begin{array}{cc}0& \frac{1}{C}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\end{array}$$
其中$\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$为选取的中间变量，又称为状态变量，表示了在不同情况下系统内部情况。$u$为输入变量，$y$为输出变量，矩阵方程组中第一个方程表示了状态变量和输入变量的关系，称为状态方程，第二个方程表示了状态变量与输出变量之间的关系，称为输出方程。

抽象出上面几个变量，有公式：
$$\{\begin{array}{rl}\dot{x}& =Ax+Bu\\ y& =Cx+Du\end{array}$$
这便是状态空间表达式，公式中各符号表示为：

符号	说明
$A_n$	状态矩阵
$B_{nr}$	输入矩阵
$C_{mn}$	输出矩阵
$D_{mr}$	直接转移矩阵
$x$	状态变量
$u$	输入变量
$y$	输出变量

其中，状态变量是足以完全表征系统运动状态的最小个数的一组变量，对于n阶微分方程，对应的独立变量应该有n个，通过这n个相互独立的状态变量的方程，便可以完整地描述系统的动态变化。例如：对于一个输入变量为位移，输出变量为加速度的物理系统，对于这个二阶运动系统，其两个独立状态变量可以是速度、加速度，通过了解不同位移输入下速度和加速度的变化，建立起状态方程（因为站在巨人的肩膀上，我们不假思索地基于牛顿运动定律列出了速度-加速度方程以及速度-位移方程，通过待定系数法代入求解变量系数。这便是基于选取速度、加速度这两个具有物理意义的表达式作为状态变量建立起来的状态方程）。该方程依托输入变量位移、状态变量速度和加速度，清晰地描述出整个物理系统的内外部结构及任意时刻系统的行为。
状态空间是指以状态变量作为坐标轴所构成的一个多维空间。状态矢量是状态变量组成的列向量，状态矢量在状态空间上的一个取值，表示了系统的一个状态。
状态变量构成的一阶微分方程组称为状态方程，状态方程把系统表示为多个一阶微分方程的形式，把系统运动状态映射到了一个以状态变量为坐标轴的状态空间中。
输出方程是系统输出与状态变量之间的函数关系式，一个完整的状态空间表达式包括状态方程和输出方程。

连续时间模型之间的转换

上面简单介绍了连续时间系统的状态空间表达式描述。众所周知，连续时间系统还可以由微分方程、传递函数以及框图的形式描述。各种描述之间理论上应该可以相互转换。通过微分方程或者传递函数建立系统的状态空间表达式的问题叫做实现问题。相应的，通过系统的微分方程或者传递函数求解状态空间模型称之为系统的实现。下面将基于单输入单输出（SISO）线性时不变系统（LTI），重点叙述其他模型如何转换为状态空间模型。通常把没有零极点对消的传递函数的实现称为最小实现，本文叙述的内容均基于最小实现问题。

传递函数中无零点的实现

传递函数中无零点的微分方程可以表示为：
$$y^{(n)}+a_{n-1}{y}^{(n-1)}+\cdots +a_1\dot{y}+a_{0}y=b_{0}u(t)$$
对应的传递函数为：
$$W(s)=\frac{b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0}$$
取输出变量及其各阶导数为状态变量，即：
$$\{\begin{array}{l}{x}_1=y\\ x_2=\dot{y}\\ x_3=\ddot{y}\\ \dots \\ x_n=y^{(n-1)}\end{array}$$
即有状态方程为：
$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ \dots \\ {\dot{x}}_{n-1}=x_n\\ {\dot{x}}_n=-a_0{x}_1-a_1{x}_2-\cdots -a_{n-2}{x}_{n-1}-a_{n-1}{x}_n+b_{0}u\end{array}$$
输出方程为：
$$y=x_1$$
表示为矩阵形式有：
$$\{\begin{array}{l}\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ ⋮\\ {\dot{x}}_{n-1}\\ {\dot{x}}_n\end{array}\right)=\left(\begin{array}{ccccc}0& 1& 0& \dots & 0\\ 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & 1\\ -a_0& -a_1& -a_2& \dots & -a_{n-1}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ b_0\end{array}\right)u\\ y=\underset{\mathbf{c}}{\underbrace{[1,0,0,\dots ,0]}}\mathbf{x}\end{array}$$

其中，像上述状态方程中的状态矩阵一样主对角线上方的元素均为1、最后一行元素任意取值、其他元素均为0的矩阵称为友矩阵。

传递函数中有零点的实现

传递函数中有零点的微分方程可以表示为：
$$y^{(n)}+a_{n-1}{y}^{(n-1)}+\cdots +a_1\dot{y}+a_{0}y=b_m{u}^{(m)}+b_{m-1}{u}^{(m-1)}+\cdots +b_1\dot{u}+b_{0}u$$
对应的传递函数为：
$$W(s)=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0},m\le n$$
这里要求$m\le n$是因为我们讨论的模型应该是物理可行的。$m>n$条件下，输出变量$y$需要根据输入变量$x$的导数得出，不具有因果性，非物理可实现的。
这里，$m=n$是$m\le n$的特殊情况，我们直接讨论$m=n$的情况，同时为了方便说明和理解，首先考虑$m=n=3$的情况。

3阶系统的实现

对于传递函数：
$$W(s)=\frac{Y(s)}{U(s)}=\frac{b_3{s}^3+b_2{s}^2+b_{1}s+b_0}{s^3+a_2{s}^2+a_{1}s+a_0}$$
提出一个常数有：
$$W(s)=\frac{Y(s)}{U(s)}=b_3+\frac{(b_2-a_2{b}_3)s^2+(b_1-a_1{b}_3)s+(b_0-a_0{b}_3)}{s^3+a_2{s}^2+a_{1}s+a_0}$$
即：
$$Y(s)=b_{3}U(s)+\frac{(b_2-a_2{b}_3)s^2+(b_1-a_1{b}_3)s+(b_0-a_0{b}_3)}{s^3+a_2{s}^2+a_{1}s+a_0}U(s)$$
令$Y_1(s)=\frac{1}{s^3+a_2{s}^2+a_{1}s+a_0}U(s)$，则有：
$$Y(s)=b_{3}U(s)+\left[(b_2-a_2{b}_3)s^2+(b_1-a_1{b}_3)s+(b_0-a_0{b}_3)\right]Y_1(s)$$
两边求拉氏反变换，得到：
$$y=b_{3}u+(b_2-a_2{b}_3){\ddot{y}}_1+(b_1-a_1{b}_3){\dot{y}}_1+(b_0-a_0{b}_3)y_1$$
这样，一个传递函数有零点的实现问题便被转换为传递函数无零点的实现问题。其中，$y_1$为$Y_1(s)$的拉氏反变换，有：

$${\stackrel{...}{y}}_1(t)+a_2{\ddot{y}}_1(t)+a_1{\dot{y}}_1(t)+a_0{y}_1(t)=u(t)$$
状态变量选取$y_1$及其各阶导数，有：

$$\{\begin{array}{l}{x}_1=y_1\\ x_2={\dot{y}}_1\\ x_3={\ddot{y}}_1\end{array}$$
即有状态空间表达式为：

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ {\dot{x}}_3=-a_0{x}_1-a_1{x}_2-a_2{x}_3+u\\ y=b_{3}u+(b_2-a_2{b}_3)x_3+(b_1-a_1{b}_3)x_2+(b_0-a_0{b}_3)x_1\end{array}$$
表示为矩阵形式有：
$$\{\begin{array}{l}\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right)=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -a_0& -a_1& -a_2\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)u\\ y=\left(\begin{array}{ccc}{b}_0-a_0{b}_3& b_1-a_1{b}_3& b_2-a_2{b}_3\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)+b_{3}u\end{array}$$

推广到$n$阶系统的实现

对于n阶传递函数：

$$W(s)=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0},m\le n$$
对应的微分方程为：

$$y^{(n)}+a_{n-1}{y}^{(n-1)}+\cdots +a_1\dot{y}+a_{0}y=b_m{u}^{(m)}+b_{m-1}{u}^{(m-1)}+\cdots +b_1\dot{u}+b_{0}u$$
其状态空间表达式为：
$$\{\begin{array}{l}\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ ⋮\\ {\dot{x}}_{n-1}\\ {\dot{x}}_n\end{array}\right)=\left(\begin{array}{ccccc}0& 1& 0& \dots & 0\\ 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & 1\\ -a_0& -a_1& -a_2& \dots & -a_{n-1}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right)u\\ y=\left(\begin{array}{ccccc}{b}_0-a_0{b}_n& b_1-a_1{b}_n& \dots & b_{n-2}-a_{n-2}{b}_n& b_{n-1}-a_{n-1}{b}_n\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+b_{n}u\end{array}{b}_n=0当n>m$$

状态空间表达式的非唯一性

对于任意一个系统，其状态空间表达式描述了系统的内部性质。而对于给定一个时不变系统，可以选取多个状态变量的组合，对应会出现多种状态空间表达式的表现形式，即一个系统可以有多个状态空间表达式，各状态空间表达式对应的状态矢量彼此之间应该是线性相关，可以通过坐标变换相互转换。下面给予上述表述数学证明：

设给定系统：
$$\{\begin{array}{rl}\dot{x}& =Ax+Bu,x(0)=x_0\\ y& =Cx+Du\end{array}$$
总可以找到任意一个非奇异矩阵$T$，将原状态矢量$x$作线性变换，得到另一状态矢量$z$，设变换关系为：
$$x=Tz$$
即
$$z=T^{-1}x$$
代入原状态空间表达式，得到新的状态空间表达式：
$$\{\begin{array}{rl}\dot{z}& =T^{-1}ATz+T^{-1}Bu,z(0)=T^{-1}\mathbf{x}(0)=T^{-1}{\mathbf{x}}_0\\ y& =CTz+Du\end{array}$$
由于$T$为任意非奇异矩阵，故状态空间表达式是非唯一的。通常称$T$为变换矩阵。

状态空间表达式的标准型

我们了解到传递函数和微分方程表示的只是系统的外部性质，其内部实现并不是唯一的，即建立起的状态空间表达式也具有非唯一性。为了简化控制系统的分析与设计，规范化矩阵形式，现代控制理论中规定了集中具有固定结构规律的规范化的状态空间表达式的形式，这些形式被称为状态空间表达式的标准型。状态空间表达式的标准型核心分为三大类：

• 能控标准型
• 能观标准型
• 对角标准型/约当标准型

对角标准型/约当标准型

对角矩阵和约当矩阵

对角矩阵和约当矩阵是线性代数中两个特殊矩阵。其中，对角矩阵为：
$$A=\text{diag}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n)=\left(\begin{array}{cccc}{\lambda }_1& 0& \dots & 0\\ 0& {\lambda }_2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\lambda }_n\end{array}\right)$$
${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$是对角矩阵的主对角线元素（可重复）。
约当矩阵是对角矩阵的自然推广，对于不可对角化的矩阵（几何重数小于代数重数），常常使用约当矩阵构建分块对角矩阵，实现其标准化需求。约当矩阵的基本单元为“约当块”，约当块的定义如下：
设 $\lambda \in \mathbb{F}$，对正整数$k$，称$k$阶方阵：
$$J_k(\lambda )=\left(\begin{array}{ccccc}\lambda & 1& 0& \dots & 0\\ 0& \lambda & 1& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & 1\\ 0& 0& 0& \dots & \lambda \end{array}\right)$$
为对应特征值$\lambda$的$k$阶约当块。约当块的一条副对角线值为1，上下副对角线都可以，但是所有约当块选取的副对角线需相同。

在此基础上，约当矩阵的定义有：
若一个方阵$J\in {\mathbb{F}}^{n\times n}$可以表示为分块对角矩阵，且每个分块都是约当块，则称$J$为约当矩阵，即：
$$J=\left(\begin{array}{cccc}{J}_{k_1}({\lambda }_1)& 0& \dots & 0\\ 0& J_{k_2}({\lambda }_2)& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & J_{k_m}({\lambda }_m)\end{array}\right)$$
其中：
$k_1+k_2+\cdots +k_m=n$，即分块的阶数之和等于矩阵总阶数；${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_m$是数域$\mathbb{F}$中的元素（可重复，对应特征值）；约当块的顺序不唯一。

状态空间表达式的对角标准型和约当标准型

由于本文的实现问题都是最小实现问题，能转化为对角标准型的实现不存在重根。也就是说，存在重根的实现问题只能转换为约当标准型。从这个角度看，对角标准型是约当标准型的一个特殊情况（即无重根的约当标准型）。而所谓状态空间表达式转换为约当标准型，实际上是原状态空间表达式通过矩阵变换，使得状态矩阵变换为约当矩阵的形式。

一般实现转换为约当标准型

前面我们描述了状态空间表达式的非唯一性，下面我们基于此叙述一般状态空间表达式转换为约当标准型状态空间表达式的问题：
对于实现：
$$\{\begin{array}{l}\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}\\ \mathbf{y}=\mathbf{C}\mathbf{x}\end{array}$$
要求通过非奇异矩阵$T$，有$x=zT$，代入原方程组，使之变换为形式：
$$\{\begin{array}{l}\dot{\mathbf{z}}=\mathbf{J}\mathbf{z}+{\mathbf{T}}^{-1}\mathbf{B}\mathbf{u}\\ \mathbf{y}=\mathbf{C}\mathbf{T}\mathbf{z}\end{array}$$
其中$J$为约旦标准型矩阵，无重根时：
$$\mathbf{J}=\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)$$
有重根时（$q+1$个重根）：
$$J=\left(\begin{array}{ccccccc}{\lambda }_1& 1& 0& \cdots & & & \\ 0& {\lambda }_1& 1& \cdots & & & \\ & 0& {\lambda }_1& \ddots & & & \\ & & \ddots & \ddots & 1& & \\ & & & 0& {\lambda }_1& & \\ & & & & & {\lambda }_{q+1}& \\ & & & & & \ddots & \\ & & & & & & {\lambda }_n\end{array}\right)$$
所以，问题就变成了求奇异矩阵$T$，使变换$T^{-1}AT$为约当矩阵，这里就不加说明了。

传递函数的约当标准型实现

对角标准型实现

对于可以转换为对角标准型的传递函数：
$$G(s)=\frac{Y(s)}{U(s)}=\frac{b_n{s}^n+b_{n-1}{s}^{n-1}+\cdots +b_{1}s+b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0}$$
其特征方程无重根，故可以把$G(s)$分解因式得到如下形式：
$$G(s)=\frac{c_1}{s-{\lambda }_1}+\frac{c_2}{s-{\lambda }_2}+\cdots +\frac{c_n}{s-{\lambda }_n}+b_n$$
其中${\lambda }_1,{\lambda }_2,\dots {\lambda }_n为其极点$。令
$$\{\begin{array}{l}{X}_1(s)=\frac{1}{s-{\lambda }_1}U(s)\\ X_2(s)=\frac{1}{s-{\lambda }_2}U(s)\\ ⋮\\ X_n(s)=\frac{1}{s-{\lambda }_n}U(s)\end{array}$$
则有状态变量：
$$\{\begin{array}{l}{x}_1=e^{{\lambda }_{1}t}\\ x_2=e^{{\lambda }_{1}t}\\ ⋮\\ x_n=e^{{\lambda }_{n}t}\end{array}$$
可得系统的状态方程为：
$$\{\begin{array}{l}{\dot{x}}_1={\lambda }_1{x}_1+u\\ {\dot{x}}_2={\lambda }_2{x}_2+u\\ ⋮\\ {\dot{x}}_n={\lambda }_n{x}_n+u\end{array}$$
矩阵表示为：
$$\dot{\mathbf{x}}=\left(\begin{array}{ccccc}{\lambda }_1& 0& \cdots & 0& 0\\ 0& {\lambda }_2& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & {\lambda }_{n-1}& 0\\ 0& 0& \cdots & 0& {\lambda }_n\end{array}\right)\mathbf{x}+\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\\ 1\end{array}\right)u$$
输出方程为：
$$y=\left(\begin{array}{ccccc}{c}_1& c_2& \cdots & c_{n-1}& c_n\end{array}\right)\mathbf{x}$$
故其状态空间表达式为：
$$\{\begin{array}{l}\dot{\mathbf{x}}=\left(\begin{array}{ccccc}{\lambda }_1& 0& \cdots & 0& 0\\ 0& {\lambda }_2& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & {\lambda }_{n-1}& 0\\ 0& 0& \cdots & 0& {\lambda }_n\end{array}\right)\mathbf{x}+\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\\ 1\end{array}\right)u\\ y=\left(\begin{array}{ccccc}{c}_1& c_2& \cdots & c_{n-1}& c_n\end{array}\right)\mathbf{x}\end{array}$$

约当标准型实现

对于传递函数有重根的情况，其传递函数$G(s)$可以因式分解为形式：
$$G(s)=\frac{c_{11}}{(s-{\lambda }_1{)}^r}+\frac{c_{12}}{(s-{\lambda }_1{)}^{r-1}}+\cdots +\frac{c_{1r}}{s-{\lambda }_1}+\frac{c_{r+1}}{s-{\lambda }_{r+1}}+\cdots +\frac{c_n}{s-{\lambda }_n}$$
其中，${\lambda }_1$是其$r$重根，以此类推。令：
$$\{\begin{array}{l}{X}_1(s)=\frac{1}{(s-{\lambda }_1{)}^r}U(s)\\ X_2(s)=\frac{1}{(s-{\lambda }_1{)}^{r-1}}U(s)\\ ⋮\\ X_r(s)=\frac{1}{s-{\lambda }_1}U(s)\\ X_{r+1}(s)=\frac{1}{s-{\lambda }_{r+1}}U(s)\\ ⋮\\ X_n(s)=\frac{1}{s-{\lambda }_n}U(s)\end{array}$$
即系统状态变量为：
$$\{\begin{array}{l}{x}_1=\frac{t^{r-1}}{(r-1)!}{e}^{{\lambda }_{i}t}\\ x_2=\frac{t^{r-2}}{(r-2)!}{e}^{{\lambda }_{i}t}\\ ⋮\\ x_r=e^{{\lambda }_{1}t}\\ x_{r+1}=e^{{\lambda }_{r+1}t}\\ ⋮\\ x_n=e^{{\lambda }_{n}t}\end{array}$$
有系统状态空间表达式为：
$$\{\begin{array}{l}\dot{\mathbf{x}}={\left(\begin{array}{cccccc}{\lambda }_1& 1& 0& \cdots & 0& 0\\ 0& {\lambda }_1& 1& 0& \cdots & 0\\ ⋮& & \ddots & \ddots & & ⋮\\ & & & {\lambda }_1& 1& \\ & & & & {\lambda }_{r+1}& \ddots \\ 0& 0& \cdots & 0& & {\lambda }_n\end{array}\right)}_{n\times n}\mathbf{x}+\underset{其中重根对应系数为0，单根对应系数为1}{\underbrace{{\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\\ ⋮\\ 1\end{array}\right)}_{n\times 1}}}\mathbf{u}\\ \mathbf{y}={\left(\begin{array}{cccccccc}{c}_{11}& c_{12}& \cdots & c_{1r}& c_{r+1}& \cdots & c_{n-1}& c_n\end{array}\right)}_{1\times n}\mathbf{x}\end{array}$$

系统的能控性和能观性

前面讨论过：状态方程和输出方程分别描述了随时间变化的输入$u(t)$引起状态$x(t)$的变化过程以及状态$x(t)$引起输出$y(t)$变化的过程。其中输入变量引起的状态变量变化程度被称为能控性（输入变量对状态变量的控制能力），由于状态变量变化导致的输出变量变化被称为能观性（输出变量对状态变量的反应能力），下面基于单输入单输出（SISO）线性时不变系统（LTI），分别详细叙述系统的能控性和能观性。

系统的能控性

关于线性连续定常系统（即线性时不变系统LTI），其能控性定义有：

如果存在一个分段连续的输入$u(t)$能在有限时间区间$[t_0,t_f]$内，使系统由某一初始状态$x(t_0)$，转移到指定的任一终端状态$x(t_f)$，则称此状态是能控的。若系统的所有状态都是能控的，则称此系统是状态完全能控的，简称系统是能控的。

定义看起来十分抽象，简单解释，就是能控系统的所有状态变量均可唯一地由输入变量的函数表示。下面分别看两个框图即可了然：

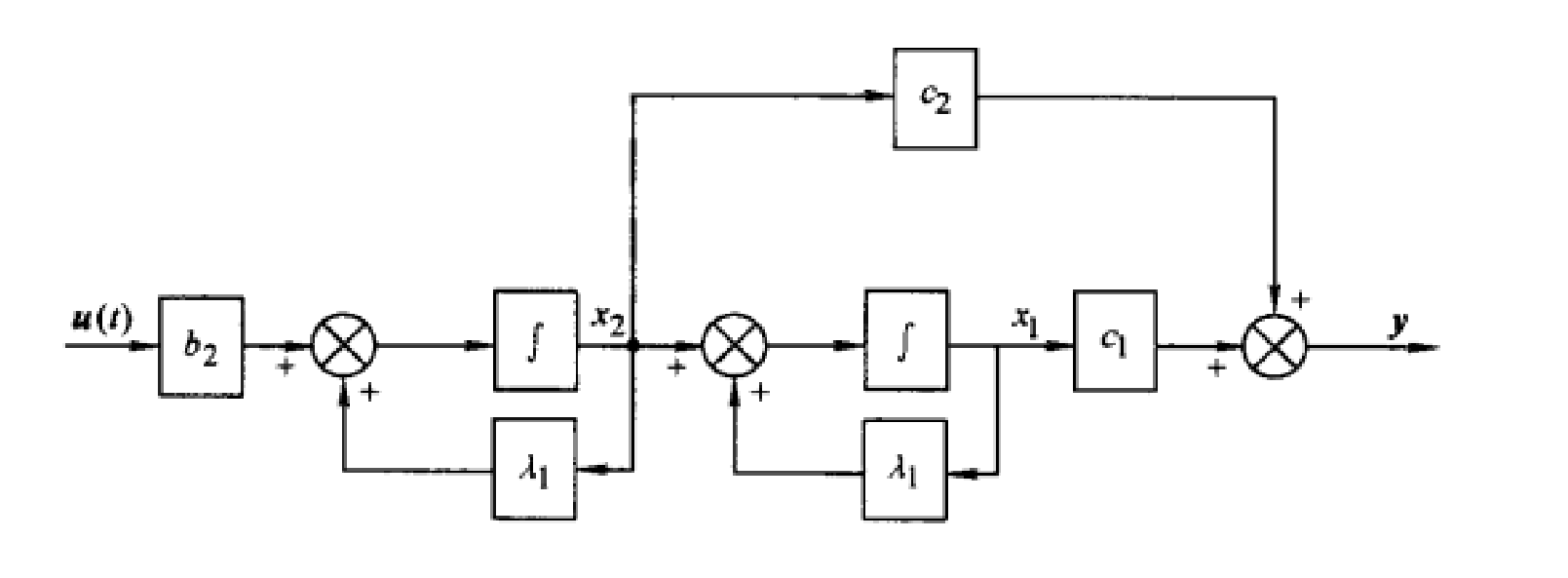
上图中，选取了两个相互独立的状态变量，状态变量均可由输入$u(t)$的函数直接表示，即系统是完全能控的。

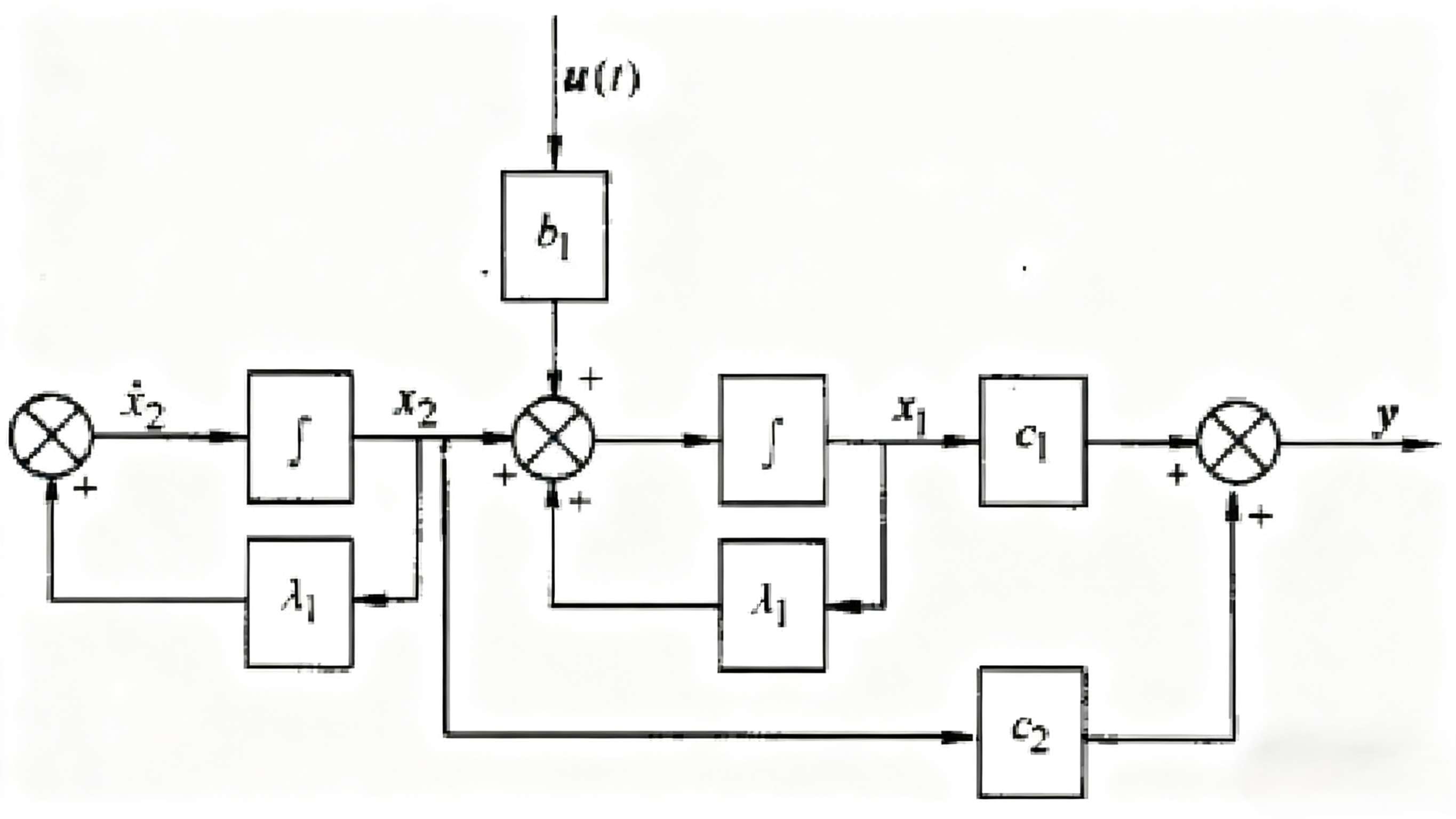
对于这个系统框图，其状态变量$x_2$不能由输入变量直接表示，即系统是不完全能控的。

系统的能观性

系统的能观性表征的是输出变量的变化是否能体现状态变量的变化，即能否通过对输出的测量获取状态变化的信息。其定义如下：

如果对于任意给定的输入$u$，在有限观测时间$t_f>t_0$，使得根据$[t_0,t_f]$期间的输出$y(t)$能唯一确定系统在初始状态$x(t_0)$，则称状态$x(t_0)$是能观测的。若系统的每一个状态都是能观测的，则称系统是状态完全能观测的，简称能观。

能控标准型和能观标准型实现

在前面描述微分方程和传递函数的实现时，实际上已经描述了能控标准型的实现，能观标准型可以记为能控标准型的转置实现，下面只给出结果（基于传递函数）：
对于传递函数：
$$W(s)=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0},m\le n$$
其能控标准型实现为：
$$\{\begin{array}{l}\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ ⋮\\ {\dot{x}}_{n-1}\\ {\dot{x}}_n\end{array}\right)={\left(\begin{array}{ccccc}0& 1& 0& \dots & 0\\ 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & 1\\ -a_0& -a_1& -a_2& \dots & -a_{n-1}\end{array}\right)}_{n\times n}\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right)u\\ y=\left(\begin{array}{ccccc}{b}_0-a_0{b}_n& b_1-a_1{b}_n& \dots & b_{n-2}-a_{n-2}{b}_n& b_{n-1}-a_{n-1}{b}_n\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+b_{n}u\end{array}{b}_n=0当n>m$$
其能观标准型实现为：
$$\{\begin{array}{l}\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ ⋮\\ {\dot{x}}_{n-1}\\ {\dot{x}}_n\end{array}\right)={\left(\begin{array}{ccccc}0& 0& \dots & 0& -a_0\\ 1& 0& \ddots & 0& -a_1\\ 0& 1& \ddots & 0& -a_2\\ ⋮& \ddots & \ddots & 0& ⋮\\ 0& \dots & 0& 1& -a_{n-1}\end{array}\right)}_{n\times n}\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+\left(\begin{array}{c}{b}_0-a_0{b}_n\\ b_1-a_1{b}_n\\ ⋮\\ b_{n-2}-a_{n-2}{b}_n\\ b_{n-1}-a_{n-1}{b}_n\end{array}\right)u\\ y=\left(\begin{array}{ccccc}0& 0& \dots & 0& 1\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)+b_{n}u\end{array}{b}_n=0当n>m$$