【信号处理】再话卷积
在【信号处理】卷积一文中,我们简单讨论了卷积作为一种数学运算可以被看作在一定条件下对原信号作线性变换(例如对于时域下LTI信号 x ( t ) x_(t) x(t),通过与同样是LTI信号的 h ( t ) h(t) h(t)卷积得到新的信号 y ( t ) y(t) y(t),可以看作 h ( t ) h(t) h(t)是一个线性系统的描述(输入的冲激响应), x ( t ) x(t) x(t)和 y ( t ) y(t) y(t)分别对应系统的输入和输出)。其中更多是从数学角度出发的,在实际应用中,卷积在不同场景中所表现的物理意义不同。本文重点讨论一维LTI信号的时域卷积和频域卷积的物理意义,以求进一步加深对卷积的理解。
时域卷积
对于两个LTI信号
x
(
t
)
x(t)
x(t)和
h
(
t
)
h(t)
h(t),有其在时域上的卷积为:
y
(
t
)
=
x
(
t
)
∗
h
(
t
)
=
∫
−
∞
+
∞
x
(
τ
)
h
(
t
−
τ
)
d
τ
y(t) = x(t) * h(t) = \int_{-\infty}^{+\infty} x(\tau) h(t - \tau) \, d\tau
y(t)=x(t)∗h(t)=∫−∞+∞x(τ)h(t−τ)dτ
这里我们不妨令
h
(
t
)
=
u
(
t
)
−
u
(
t
−
t
0
)
t
0
∈
R
h(t)=u(t)-u(t-t_0) \quad t_0 \in \mathbb{R}
h(t)=u(t)−u(t−t0)t0∈R
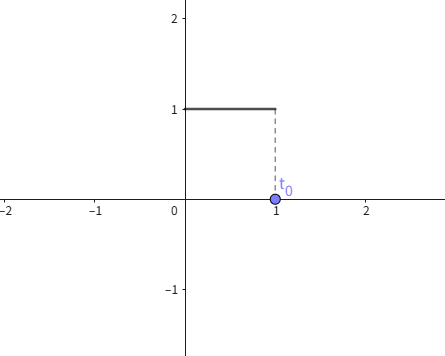
当
t
0
=
1
t_0=1
t0=1时,其图像为
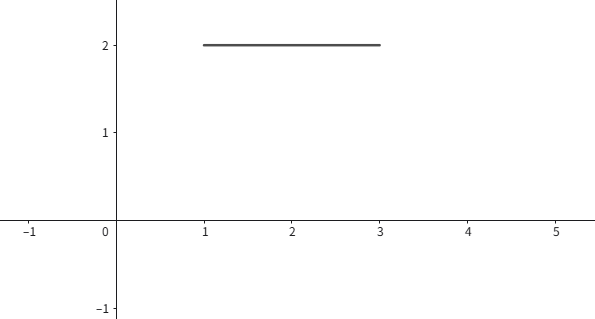
若有
x
(
t
)
x(t)
x(t)表示如下图:
则由图解法可得其卷积为:
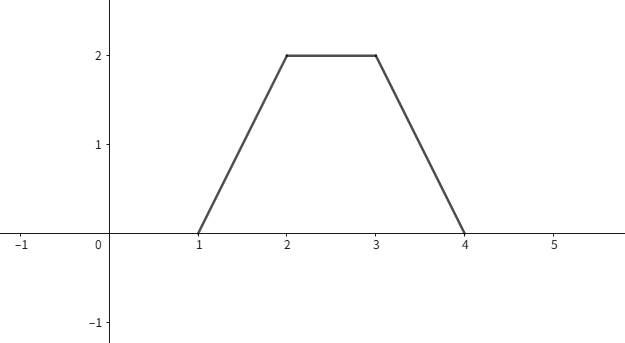
是一个梯形函数。这里,我们注意到若
h
(
t
)
h(t)
h(t)是一个矩形函数,则有
x
(
t
)
x(t)
x(t)对
h
(
t
)
h(t)
h(t)作卷积后得到的输出
y
(
t
)
y(t)
y(t)在任意点
t
1
t_1
t1的输出
y
(
t
1
)
y(t_1)
y(t1)都是输入在过去
t
0
t_0
t0时间内的积分,即
y
(
t
1
)
=
∫
t
1
−
t
0
t
1
x
(
t
)
d
t
y(t_1) = \int_{t_1-t_0}^{t_1}x(t)\,dt
y(t1)=∫t1−t0t1x(t)dt
即时域卷积起到一个累积叠加的效果,这里通过离散卷积能更清楚地看出:
令
h
[
n
]
h[n]
h[n]为:

x
[
n
]
x[n]
x[n]为:
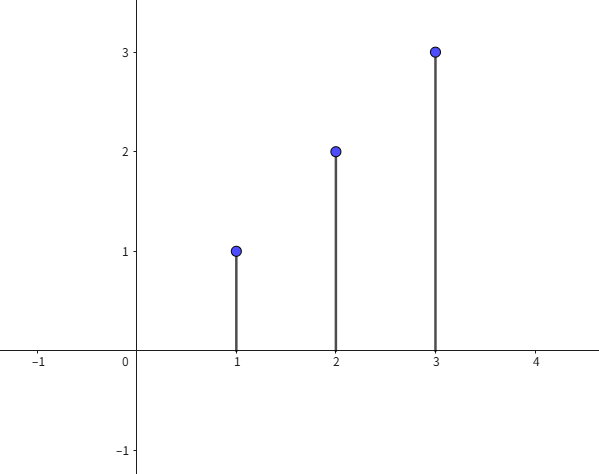
则有输出
y
[
n
]
y[n]
y[n]为:
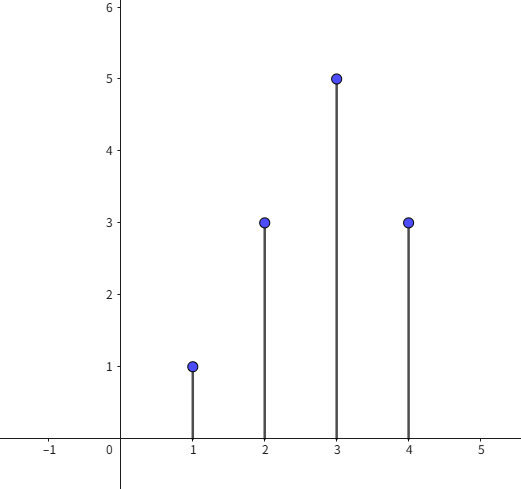
故有通过时域卷积的方式,我们能更便捷明了地实现线性系统的构建与描述。例如,对于单输入单输出(SISO)系统,如果需要对输入作倍乘输出。只需要把输入对
k
δ
(
t
)
k\delta(t)
kδ(t)作卷积即可;如果需要对输入作累积观测(作积分),只需要把输入对
u
(
t
−
t
0
)
−
u
(
t
−
t
1
)
u(t-t_0)-u(t-t_1)
u(t−t0)−u(t−t1)作卷积即可得到过去
(
−
t
1
,
−
t
0
)
(-t_1,-t_0)
(−t1,−t0)时间段的积分结果;如果需要观测输入趋势(求导数),只需要把输入对冲激偶函数
δ
′
(
t
)
\delta^{'}(t)
δ′(t)作卷积即可。
时域和频域可以看作同一信号的两个不同的观测角度。往往我们从一个视角无法理解的问题换一个角度就变得通俗易懂了(这里我不禁想起小学课本中《画杨桃》一文就十分接地气地阐述了这个哲理)。而在这里,我们发现在时域上使用卷积可以方便地实现系统的描述。但是,与之相随的是,卷积在时域上的计算比较抽象和困难。所以,伟大的先贤们探索出一个在频域上解决这个问题的方法,即卷积定理:
x
(
t
)
∗
y
(
t
)
⟺
F
[
x
(
t
)
]
⋅
F
[
y
(
t
)
]
x(t) * y(t) \iff \mathcal{F}\left[x(t)\right] \cdot \mathcal{F}\left[y(t)\right]
x(t)∗y(t)⟺F[x(t)]⋅F[y(t)]
也就是常说的时域上的卷积对应于频域上的乘积(还有频域卷积定理,这里就不加赘述了)。
总结来说,我们可以很容易地理解信号在时域上的卷积就是构造时域信号的线性系统,但是无法很容易地计算出来;我们不能直接理解信号在频域上的乘积有什么意义,但是可以很方便地因此计算出对应的时域中的卷积。
频域卷积
在了解了时域卷积后,频域卷积也就比较容易理解了。频域卷积同样可以看作输入信号通过一个频域上的线性系统。通过这个线性系统,我们就可以实现信号的频谱搬移与叠加。
故无论在哪个域,若要了解两个信号卷积的实际意义,首先最好知晓这两个信号及其傅里叶变换的特征,从而能够分别从时域和频域去考量其产生的影响。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号