【信号处理】信号的采样与重建
在【信号处理】再话卷积一文中,我们提到对信号做卷积就相当于对其作线性变换,可以在不同域中实现信号的平移、伸缩等变换操作。而根据卷积定理,对于时域或频域中的卷积,可以映射为另一域中的乘积操作。而我们所谓的采样,可以视为信号在时域内与周期单位冲激信号或周期窄脉冲信号相乘。通过结合卷积定理,我们在理解采样的同时,还可以了解其在对应域的深层含义。
时域采样
对于连续时间信号
x
a
(
t
)
x_a(t)
xa(t),其理想采样可以表示为与周期性单位冲激信号
δ
T
(
t
)
\delta_T(t)
δT(t)的乘积,即:
x
^
a
(
t
)
=
x
a
(
t
)
∑
n
=
−
∞
∞
δ
(
t
−
n
T
)
=
∑
n
=
−
∞
∞
x
a
(
t
)
δ
(
t
−
n
T
)
=
∑
n
=
−
∞
∞
x
a
(
n
T
)
δ
(
t
−
n
T
)
\begin{align*} \hat{x}_a(t) &= x_a(t) \sum_{n=-\infty}^{\infty} \delta(t - nT) \\ &= \sum_{n=-\infty}^{\infty} x_a(t) \delta(t - nT) \\ &= \sum_{n=-\infty}^{\infty} x_a(nT) \delta(t - nT) \end{align*}
x^a(t)=xa(t)n=−∞∑∞δ(t−nT)=n=−∞∑∞xa(t)δ(t−nT)=n=−∞∑∞xa(nT)δ(t−nT)

也即在频域与
F
[
δ
T
(
t
)
]
\mathcal{F}[\delta_T(t)]
F[δT(t)]的卷积(由上式左右分别取傅里叶变换可知)。令:
{
X
a
(
j
Ω
)
=
F
[
x
a
(
t
)
]
Δ
T
(
j
Ω
)
=
F
[
δ
T
(
t
)
]
X
^
a
(
j
Ω
)
=
F
[
x
^
a
(
t
)
]
\begin{cases} X_a(j\Omega) = \mathcal{F}\left[ x_a(t) \right] \\ \Delta_T(j\Omega) = \mathcal{F}\left[ \delta_T(t) \right] \\ \hat{X}_a(j\Omega) = \mathcal{F}\left[ \hat{x}_a(t) \right] \end{cases}
⎩
⎨
⎧Xa(jΩ)=F[xa(t)]ΔT(jΩ)=F[δT(t)]X^a(jΩ)=F[x^a(t)]
根据频域卷积定理:
X
^
a
(
j
Ω
)
=
1
2
π
[
X
a
(
j
Ω
)
∗
Δ
T
(
j
Ω
)
]
\hat{X}_a(j\Omega) = \frac{1}{2\pi} \left[ X_a(j\Omega) * \Delta_T(j\Omega) \right]
X^a(jΩ)=2π1[Xa(jΩ)∗ΔT(jΩ)]
这里我们只需要求解
Δ
T
(
j
Ω
)
\Delta_T(j\Omega)
ΔT(jΩ),由于
Δ
T
(
j
Ω
)
\Delta_T(j\Omega)
ΔT(jΩ)是
δ
T
(
t
)
\delta_T(t)
δT(t)的傅里叶变换,而
δ
T
(
t
)
\delta_T(t)
δT(t)是
δ
(
t
)
\delta(t)
δ(t)的周期延拓。我们知道,
F
[
δ
(
t
)
]
=
1
\mathcal{F}[\delta(t)]=1
F[δ(t)]=1,在频谱上表现为一条均匀的在任何频率取值均为1的宽频带。而
δ
T
(
t
)
\delta_T(t)
δT(t),根据【信号处理】傅里叶变换中周期信号的傅里叶变换可知,其傅里叶变换为以T为周期在
F
[
δ
(
t
)
]
\mathcal{F}[\delta(t)]
F[δ(t)]上的等距采样。从理论上推导
δ
T
(
t
−
n
T
)
\delta_T(t-nT)
δT(t−nT)的傅里叶变换有:
由周期信号的傅里叶变换可知:
δ
T
(
t
)
=
∑
k
=
−
∞
∞
F
n
e
j
k
Ω
s
t
\delta_T(t)=\sum_{k=-\infty}^{\infty}F_ne^{jk\Omega_st}
δT(t)=k=−∞∑∞FnejkΩst
其中有
Ω
s
=
2
π
T
\Omega_s=\frac{2\pi}{T}
Ωs=T2π,且:
F
n
=
1
T
∫
−
T
2
T
2
δ
T
(
t
)
e
−
j
k
Ω
s
t
d
t
=
1
T
∫
−
T
2
T
2
∑
n
=
−
∞
∞
δ
(
t
−
n
T
)
e
−
j
k
Ω
s
t
d
t
=
1
T
∫
−
T
2
T
2
δ
(
t
)
e
−
j
k
Ω
s
t
d
t
=
1
T
\begin{align*} &F_n = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \delta_T(t) e^{-jk\Omega_s t} dt \\ &= \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \sum_{n=-\infty}^{\infty} \delta(t - nT) e^{-jk\Omega_s t} dt \\ &= \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \delta(t) e^{-jk\Omega_s t} dt = \frac{1}{T} \end{align*}
Fn=T1∫−2T2TδT(t)e−jkΩstdt=T1∫−2T2Tn=−∞∑∞δ(t−nT)e−jkΩstdt=T1∫−2T2Tδ(t)e−jkΩstdt=T1
即有:
δ
T
(
t
)
=
1
T
∑
k
=
−
∞
∞
e
j
k
Ω
s
t
\delta_T(t) = \frac{1}{T} \sum_{k=-\infty}^{\infty} e^{jk\Omega_s t}
δT(t)=T1k=−∞∑∞ejkΩst
两边分别取傅里叶变换,有:
Δ
T
(
j
Ω
)
=
F
[
1
T
∑
k
=
−
∞
∞
e
j
k
Ω
s
t
]
=
1
T
∑
k
=
−
∞
∞
F
[
e
j
k
Ω
s
t
]
=
2
π
T
∑
k
=
−
∞
∞
δ
(
Ω
−
k
Ω
s
)
=
Ω
s
∑
k
=
−
∞
∞
δ
(
Ω
−
k
Ω
s
)
\begin{align*} &\Delta_T(j\Omega) = \mathcal{F}\left[ \frac{1}{T} \sum_{k=-\infty}^{\infty} e^{jk\Omega_s t} \right] = \frac{1}{T} \sum_{k=-\infty}^{\infty} \mathcal{F}\left[ e^{jk\Omega_s t} \right] \\ &= \frac{2\pi}{T} \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_s) = \Omega_s \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_s) \end{align*}
ΔT(jΩ)=F[T1k=−∞∑∞ejkΩst]=T1k=−∞∑∞F[ejkΩst]=T2πk=−∞∑∞δ(Ω−kΩs)=Ωsk=−∞∑∞δ(Ω−kΩs)
即:
Δ
T
(
j
Ω
)
=
Ω
s
∑
k
=
−
∞
∞
δ
(
Ω
−
k
Ω
s
)
\Delta_T(j\Omega)=\Omega_s\sum_{k=-\infty}^{\infty}\delta(\Omega-k\Omega_s)
ΔT(jΩ)=Ωsk=−∞∑∞δ(Ω−kΩs)
值得关注的是,
δ
T
(
t
)
\delta_T(t)
δT(t)及其傅里叶变换均为周期性离散分布的等值脉冲,这是一个十分良好且独特的性质(当然也是理想的性质)。在时域上,
δ
T
(
t
)
\delta_T(t)
δT(t)与原信号相乘,实现时域采样,而在频域上,原信号与
Δ
T
(
j
Ω
)
\Delta_T(j\Omega)
ΔT(jΩ)卷积,表现为在以
Ω
s
\Omega_s
Ωs为间隔的周期延拓,即在
Δ
T
(
j
Ω
)
\Delta_T(j\Omega)
ΔT(jΩ)的每个采样尖峰的位置延拓一个原信号的傅里叶变换
X
a
(
j
Ω
)
X_a(j\Omega)
Xa(jΩ)。数学表示为:
X
^
a
(
j
Ω
)
=
1
2
π
[
X
a
(
j
Ω
)
∗
Δ
T
(
j
Ω
)
]
=
1
2
π
[
X
a
(
j
Ω
)
∗
(
Ω
s
∑
k
=
−
∞
∞
δ
(
Ω
−
k
Ω
s
)
)
]
=
1
T
∑
k
=
−
∞
∞
X
a
[
j
(
Ω
−
k
Ω
s
)
]
\begin{align*} &\hat{X}_a(j\Omega) = \frac{1}{2\pi} \left[ X_a(j\Omega) * \Delta_T(j\Omega) \right] \\ &= \frac{1}{2\pi} \left[ X_a(j\Omega) * \left( \Omega_s \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_s) \right) \right] \\ &= \frac{1}{T} \sum_{k=-\infty}^{\infty} X_a \left[ j(\Omega - k\Omega_s) \right] \end{align*}
X^a(jΩ)=2π1[Xa(jΩ)∗ΔT(jΩ)]=2π1[Xa(jΩ)∗(Ωsk=−∞∑∞δ(Ω−kΩs))]=T1k=−∞∑∞Xa[j(Ω−kΩs)]
奈奎斯特采样定理
前面我们说到理想的采样在时域上表现为对连续信号以采样周期T离散化,在频域上表现为对频谱作周期为
Ω
s
=
2
π
T
\Omega_s=\frac{2\pi}{T}
Ωs=T2π的延拓,信号的采样把原本有限带宽的信号加载到全频带。那么问题来了,采样频率
f
s
=
1
T
f_s = \frac{1}{T}
fs=T1取何值能够在最低频率下采样到完整可恢复信号?
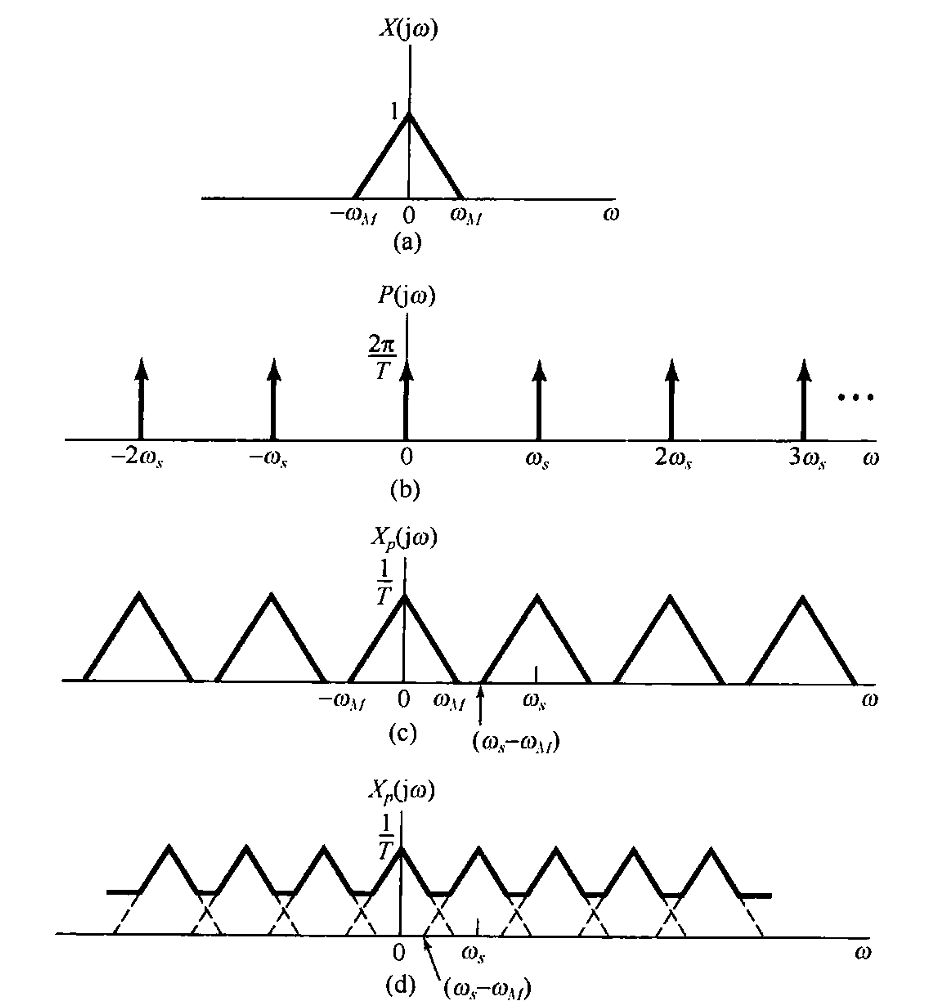
信号的傅里叶变换与原信号一一对应,其频谱对应的幅度谱与相位谱可以完备地描述出原信号,也就是说只要我们从采样后得到离散信号的频谱中能分离出原始信号的频谱便可以重建出原始信号。而由于理想采样得到的频谱是原信号频谱以
Ω
s
\Omega_s
Ωs为周期的周期延拓,理想情况下我们只需取出其一个周期即可还原出完整信号,前提是在进行周期延拓时延拓周期
Ω
s
\Omega_s
Ωs足够大,也就是采样频率
f
s
=
2
π
Ω
s
f_s=2\pi\Omega_s
fs=2πΩs足够大,使得相邻两个频谱不会重叠,从而确保单个周期的完整性。也就是
X
^
a
(
j
Ω
)
\hat{X}_a(j\Omega)
X^a(jΩ)的周期
Ω
s
\Omega_s
Ωs应大于原信号
X
a
(
t
)
X_a(t)
Xa(t)最大值
Ω
h
\Omega_h
Ωh的两倍,即:
Ω
s
>
2
Ω
h
⇒
f
s
>
2
f
h
\Omega_s>2\Omega_h \Rightarrow f_s>2f_h
Ωs>2Ωh⇒fs>2fh
这就是奈奎斯特采样定理:
若 x a ( t ) x_a(t) xa(t)是带限信号(有限带宽信号),要想采样后信号不失真地还原出原信号,必须要求采样频率 f s f_s fs大于或等于信号最高频率分量 f h f_h fh的两倍。
这里要求大于等于最高频率的两倍,那么,问题是:
- 为什么取最高频率的两倍?
这就要回到傅里叶变换的概念,同样是在【信号处理】傅里叶变换一文中说明了,傅里叶变换后得到的信号频谱拓展了负频率范围,若一个信号的通频带为 [ ω a , ω b ] [\omega_a,\omega_b] [ωa,ωb],那么傅里叶变换后得到的频率范围为 [ − ω b , − ω a ] ∨ [ ω a , ω b ] [-\omega_b,-\omega_a]\lor[\omega_a,\omega_b] [−ωb,−ωa]∨[ωa,ωb],即在数轴上占据了两倍最高频率 2 ω b 2\omega_b 2ωb的范围,故最高频率要求大于等于2倍最高频率。 - 为什么是最高频率而不是通频带?
这个问题仍然是因为存在负频率,若使用通频带其负频率的周期延拓可能与正频率的周期延拓重叠导致失真。
带通信号的采样
在讨论奈奎斯特采样定理时,我们说不失真采集原始信号要求采样频率必须高于最高频率的两倍,但是对于许多高频信号例如无线通信中的调制信号,其频率高、频带窄,如果此时仍取2倍最高频率,显然对硬件设备要求太高了。但是若只根据通带带宽采样呢?前面说过会导致正负频谱混叠,但是,还有一种可能——取合适的采样频率,使得采样得到的正负频谱交错排列。
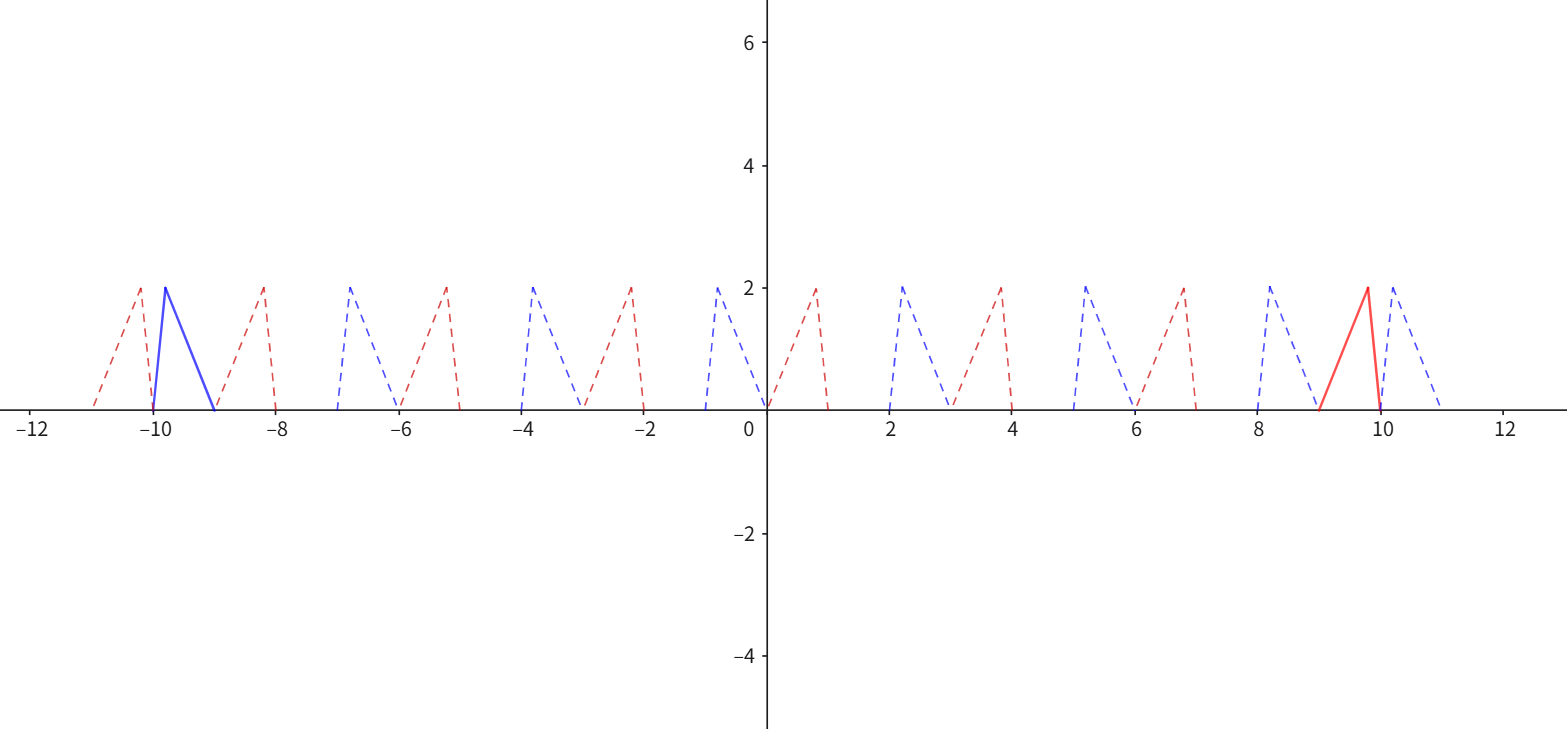
这里,我们先简单说明一下相关参数:
f
H
:
信号最高频率
f
L
:
信号最低频率
B
W
=
f
l
+
f
h
2
:
信号带宽
f
s
:
采样频率
\begin{align*} f_H&:信号最高频率 \\ f_L&:信号最低频率 \\ BW&=\frac{f_l+f_h}{2}:信号带宽 \\ f_s&:采样频率 \end{align*}
fHfLBWfs:信号最高频率:信号最低频率=2fl+fh:信号带宽:采样频率
为保证频谱不混叠,有当负频率采样后的延拓频谱与原始正频率的左右两端不发生重叠,即:
{
−
f
L
+
k
f
s
≤
f
L
−
f
H
+
(
k
+
1
)
f
s
≥
f
H
\begin{cases} -f_L+kf_s\leq f_L \\ -f_H+(k+1)f_s\geq f_H \end{cases}
{−fL+kfs≤fL−fH+(k+1)fs≥fH

这里的k取自然数,化简得:
2
f
H
k
+
1
≤
f
s
≤
2
f
L
k
\frac{2f_H}{k+1} \leq f_s \leq \frac{2f_L}{k}
k+12fH≤fs≤k2fL
当然,k的取值也应该满足一定要求,我们把
f
L
=
f
H
−
B
W
f_L=f_H-BW
fL=fH−BW代入上面的不等式,有:
2
f
H
k
+
1
≤
f
s
≤
2
(
f
H
−
B
W
)
k
\frac{2f_H}{k+1} \leq f_s \leq \frac{2(f_H-BW)}{k}
k+12fH≤fs≤k2(fH−BW)
要求
2
f
H
k
+
1
≤
2
(
f
H
−
B
W
)
k
\frac{2f_H}{k+1} \leq \frac{2(f_H-BW)}{k}
k+12fH≤k2(fH−BW)
化简后有
k
≤
B
W
k\leq BW
k≤BW,同时
k
≥
0
k \geq 0
k≥0(等于0时$\frac{2f_L}{k-1} \to \infty
),又
),又
),又k \in \mathbb{N}$,故有:
0
≤
k
≤
⌊
f
L
B
W
⌋
0\leq k \leq \left\lfloor \frac{f_L}{BW}\right\rfloor
0≤k≤⌊BWfL⌋
其中
⌊
⋅
⌋
\left\lfloor \cdot \right\rfloor
⌊⋅⌋表示向下取整。
这里的
k
k
k就可以理解为正负频谱之间负频谱或正频谱延拓周期的个数,或者说在
[
0
,
f
L
]
[0,f_L]
[0,fL]之间延拓的频谱个数(无论正负)。显然,当
k
=
0
k=0
k=0时,这之间延拓的频谱个数为0,原信号
f
L
=
0
f_L=0
fL=0,就变成了低频信号的采样定理。
总结就是:
信号的采样频率要求符合:
2 f H k + 1 ≤ f s ≤ 2 ( f H − B W ) k \frac{2f_H}{k+1} \leq f_s \leq \frac{2(f_H-BW)}{k} k+12fH≤fs≤k2(fH−BW)
其中, 0 ≤ k ≤ ⌊ f L B W ⌋ k ∈ N 0\leq k \leq \left\lfloor \frac{f_L}{BW}\right\rfloor \quad k \in \mathbb{N} 0≤k≤⌊BWfL⌋k∈N
这就是带通信号的采样定理,当
k
=
0
k=0
k=0时,定理便是低频的奈奎斯特采样定理。通过该定理,我们还可以计算出最低采样频率,即
k
k
k取到可取的最大值对应的
f
s
f_s
fs的最小值。特别地,当
f
L
f_L
fL或
f
H
f_H
fH为
B
W
BW
BW的整数倍时,有
k
m
a
x
=
f
L
B
W
k_{max}=\frac{f_L}{BW}
kmax=BWfL,即有最低采样率为:
f
s
m
i
n
=
2
f
H
f
L
+
1
B
W
=
2
B
W
{f_s}_{min}=\frac{2f_H}{\frac{f_L+1}{BW}}=2BW
fsmin=BWfL+12fH=2BW
信号的重建
在信号的采样部分,我们使用周期性单位冲激函数对原始信号采样,实现了频域上信号频谱的周期性延拓。如果要完整重建原始信号,理想情况下,只需要截取采样后频谱的一个完整周期即可。这里同样设原始信号为
x
(
t
)
x(t)
x(t),采样周期为
T
s
T_s
Ts,采样后信号为
x
^
(
t
)
\hat{x}(t)
x^(t),其对应的傅里叶变换为
X
(
j
Ω
)
X(j\Omega)
X(jΩ)和
X
^
(
j
Ω
)
\hat{X}(j\Omega)
X^(jΩ),重建后信号为
x
1
(
t
)
x_1(t)
x1(t),对应傅里叶变换为
X
1
(
j
Ω
)
X_1(j\Omega)
X1(jΩ)。
如果信号是由原始信号通过周期性冲激信号采样得到,那么,通过一个理想低通滤波器即可还原原信号,采样后信号与原始信号关系有:
x
^
(
t
)
=
x
(
t
)
δ
T
s
(
t
)
=
x
(
t
)
∑
n
=
−
∞
∞
δ
(
t
−
n
T
s
)
\begin{align*} &\hat{x}(t)=x(t)\delta_{T_s}(t) \\ &=x(t)\sum_{n=-\infty}^{\infty}\delta(t-nT_s) \end{align*}
x^(t)=x(t)δTs(t)=x(t)n=−∞∑∞δ(t−nTs)
X
^
(
j
Ω
)
=
1
2
π
[
X
(
j
Ω
)
∗
Δ
T
(
j
Ω
)
]
=
1
2
π
[
X
(
j
Ω
)
∗
(
Ω
s
∑
k
=
−
∞
∞
δ
(
Ω
−
k
Ω
s
)
)
]
=
1
T
s
∑
k
=
−
∞
∞
X
[
j
(
Ω
−
k
Ω
s
)
]
\begin{align*} &\hat{X}(j\Omega) = \frac{1}{2\pi} \left[ X(j\Omega) * \Delta_T(j\Omega) \right] \\ &= \frac{1}{2\pi} \left[ X(j\Omega) * \left( \Omega_s \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_s) \right) \right] \\ &= \frac{1}{T_s} \sum_{k=-\infty}^{\infty} X \left[ j(\Omega - k\Omega_s) \right] \end{align*}
X^(jΩ)=2π1[X(jΩ)∗ΔT(jΩ)]=2π1[X(jΩ)∗(Ωsk=−∞∑∞δ(Ω−kΩs))]=Ts1k=−∞∑∞X[j(Ω−kΩs)]
理想低通滤波器:
H
(
j
Ω
)
=
{
T
s
(
当
∣
Ω
∣
<
ω
c
)
0
(
当
∣
Ω
∣
>
ω
c
)
H(j\Omega) = \begin{cases} T_s & (当\ |\Omega| < \omega_c) \\ 0 & (当\ |\Omega| > \omega_c) \end{cases}
H(jΩ)={Ts0(当 ∣Ω∣<ωc)(当 ∣Ω∣>ωc)
h
(
t
)
=
T
s
⋅
ω
c
π
S
a
(
ω
c
t
)
h(t) = T_s\cdot\frac{\omega_c}{\pi}Sa(\omega_ct)
h(t)=Ts⋅πωcSa(ωct)
其中
ω
c
\omega_c
ωc为滤波器的截止频率,根据奈奎斯特采样定理有
ω
c
<
Ω
s
\omega_c<\Omega_s
ωc<Ωs。可以得到重建信号为:
X
1
(
j
Ω
)
=
X
^
(
j
Ω
)
⋅
H
(
j
Ω
)
=
X
[
j
Ω
]
\begin{align*} &X_1(j\Omega) = \hat{X}(j\Omega)\cdot H(j\Omega) \\ &= X[j\Omega] \end{align*}
X1(jΩ)=X^(jΩ)⋅H(jΩ)=X[jΩ]
其中
−
ω
c
<
Ω
<
ω
c
-\omega_c<\Omega<\omega_c
−ωc<Ω<ωc。得到的结果通过逆变换即与原信号相当。我们不妨同样直接从时域卷积入手,有:
x
1
(
t
)
=
x
^
(
t
)
∗
h
(
t
)
=
x
(
t
)
∑
n
=
−
∞
∞
δ
(
t
−
n
T
s
)
∗
h
(
t
)
=
∑
n
=
−
∞
∞
x
^
(
n
T
s
)
δ
(
t
−
n
T
s
)
∗
T
s
⋅
ω
c
π
S
a
(
ω
c
t
)
=
T
s
⋅
ω
c
π
∑
n
=
−
∞
∞
x
^
(
n
T
s
)
S
a
[
ω
c
(
t
−
n
T
s
)
]
\begin{align*} &x_1(t) = \hat{x}(t) * h(t) \\ &=x(t)\sum_{n=-\infty}^{\infty}\delta(t-nT_s) * h(t) \\ &= \sum_{n=-\infty}^{\infty} \hat{x}(nT_s) \delta(t - nT_s) * T_s \cdot \frac{\omega_c}{\pi} Sa(\omega_c t) \\ &= T_s \cdot \frac{\omega_c}{\pi} \sum_{n=-\infty}^{\infty} \hat{x}(nT_s) Sa\left[ \omega_c (t - nT_s) \right] \end{align*}
x1(t)=x^(t)∗h(t)=x(t)n=−∞∑∞δ(t−nTs)∗h(t)=n=−∞∑∞x^(nTs)δ(t−nTs)∗Ts⋅πωcSa(ωct)=Ts⋅πωcn=−∞∑∞x^(nTs)Sa[ωc(t−nTs)]
根据上面的结果还可以得出,原信号
x
(
t
)
x(t)
x(t)在时域上可以表示为抽样值
x
^
(
n
T
s
)
\hat{x}(nT_s)
x^(nTs)与抽样函数的周期序列
S
a
[
ω
c
(
t
−
n
T
s
)
]
Sa\left[ \omega_c (t - nT_s) \right]
Sa[ωc(t−nTs)]的加权和。
本文仅仅简单介绍了理想情况下信号的时域采样与重建,并借此进一步探讨卷积在信号采样中的作用效果、理解其在时频变换中的地位。实际情况下,采样所用函数无法实现冲激函数这种极限情况,采样和重建的具体实现与理想情况相比略有差异,具体实现将另起篇幅讨论。卷积与傅里叶变换是信号处理的两大利器,这两个方法还衍生出了许多其他的时域、频域、连续域、离散域等多种状况下的不同处理办法以及不同域之间的变换方法,是信号处理的核心与基础。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号