【信号处理】拉普拉斯变换（1）

1872年，皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace）首先在天体力学和概率统计的研究中引入类似后面的拉氏积分的形式（${\int }_0^{\infty }{e}^{-st}f(t)dt$）并奠定了该方法的数学基础。此时，该方法被用于求解微分方程。后来，傅里叶变换被提出，其基本思想是把时域信号分解为一系列正弦或余弦分量的形式以实现微分方程的求解（将时域微分方程转化为频域代数方程）。但是，变换要求原方程中各项绝对可积。拉氏变换基于该思路，通过引入复频率$s=\sigma +j\omega$（在原有实频率的基础上增加实部$\sigma$），突破了傅里叶变换要求绝对可积的限制，使之可以处理更多种类信号。1885年左右，英国工程师奥利弗·海维赛德（Oliver Heaviside）发明了”算子法“以方便解决电工程计算中的问题（如下图），算法核心思想与拉氏积分高度一致，但是缺乏严格的数学理论支持。

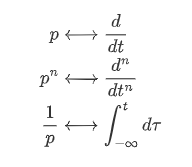
数学家们把拉普拉斯的积分理论与算子法结合，建立起严格的数学理论基础，并正式确定里普拉斯变换（Laplace Transform）的名称（简称拉氏变换）及理论体系。至此，拉氏变换开始被广泛应用于工程计算，极大简化了微分方程的求解及系统的分析与设计。

目前来说，拉普拉斯变换可以有两种理解，其一是拉氏变换是对算子法的严谨论证，并且，以拉氏变换为基础，派生出来拉氏逆变换、收敛域、零极点理论、传递函数等一系列方法构成了现代拉氏变换理论体系，该理论体系不仅用于最初的微分方程代数方程化求解问题，还被广泛应用于电路分析、系统设计与概率论等相关领域。
另一种理解是从傅里叶变换入手，也即上面说明的解决傅里叶变换的绝对可积条件的问题。实际应用中，许多信号并非绝对可积的，这些信号不能简单地直接使用傅里叶变换加以分析，故在傅里叶变换的基础上引入了一个衰减因子，把信号衰减到绝对可积后再利用傅里叶变换加以分析。
下面本文基于第二种理解，从傅里叶变换出发，分析拉普拉斯变换的原理、性质及应用。

定义

由前面的介绍可知，拉氏变换可以看作傅里叶变换的推广形式，傅里叶变换：
$$\{\begin{array}{l}F(\omega )={\int }_{-\infty }^{+\infty }f(t)e^{-j\omega t}dt\\ f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(\omega )e^{j\omega t}d\omega \end{array}$$
其成立前提是原信号绝对可积，即：
$${\int }_{-\infty }^{+\infty }|f(t)|dt<\infty$$
而在拉氏变换中，通过引入衰减因子$e^{-\sigma t}$（这里的参数$\sigma$根据原信号需求进行取值，若信号比较难以收敛，对应的$\sigma$取值也就更大），对信号作衰减处理来满足收敛条件，即：
$$F_1(\omega )={\int }_{-\infty }^{+\infty }f(t)e^{-\sigma t}{e}^{-j\omega t}$$
这里的积分区间取$(-\infty ,+\infty )$，这种形式被称为双边拉氏变换（Bilateral Laplace Transform）。一般情况下，特别是在实际工程应用中，应用到的信号和系统都是因果的，即$f(t)=0,(t<0)$，故常限制积分区间为$[0,\infty )$，令$s=\sigma +j\omega$，即
$$F(s)={\int }_0^{\infty }f(t)e^{-st}dt$$
是为单边拉普拉斯变换（Unilater Laplace Transform），也即通常意义上所指的拉氏变换。这里要求：
$${\int }_0^{\infty }|f(t)e^{-\sigma t}|dt<\infty$$
得到的$\sigma$制约条件也就是原信号拉氏变换后的收敛域，这里的收敛域只是限制了$\sigma$的取值，$\omega$的取值范围仍是$(-\infty ,+\infty )$。
拉氏逆变换同样可以由傅里叶逆变换导出，即：
$$\begin{array}{r}f(t)e^{-\sigma t}=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\sigma +j\omega )e^{j\omega t}d\omega \\ f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\sigma +j\omega )e^{(\sigma +j\omega )t}d\omega \end{array}$$
令$s=\sigma +j\omega$，$ds=d\sigma +jd\omega =jd\omega$，积分变限，得到：
$$f(t)=\frac{1}{2\pi j}{\int }_{\sigma -j\infty }^{\sigma +j\infty }F(s)e^{st}ds$$
即为拉氏逆变换。拉氏变换的符号表示为$\mathcal{L}[\cdot ]$，即有拉普拉斯变换及其逆变换为：
$$\begin{array}{rl}& \mathcal{L}\left[f(t)\right]=F(s)={\int }_0^{\infty }f(t)e^{-st}dt\\ & {\mathcal{L}}^{-1}\left[F(s)\right]=f(t)=\frac{1}{2\pi j}{\int }_{\sigma -j\infty }^{\sigma +j\infty }F(s)e^{st}ds\end{array}$$
其中，复变量$s$由两个量确定，一个是衰减因数$\sigma$，另一个是复频率$j\omega$，根据傅里叶变换的性质可知，复频率$j\omega$对应的频谱任然是关于纵轴幅度堆成，相位反相的。而衰减因数，可以理解为每个确定的衰减因数$\sigma ={\sigma }_0$，都有信号对应程度衰减后的频谱$F(j\omega ){|}_{\sigma ={\sigma }_0}$。

收敛域和极点

对于一个原信号$f(t)$不是绝对可积的信号，若衰减因数$\sigma$取值不够大，即信号衰减幅度不够大，衰减后仍然无法实现绝对可积（对于原本满足绝对可积的信号，通过对衰减因数取负值，反向衰减（即放大）信号，同样可以达到不满足绝对可积的情况）。这种情况下对应的频谱$F(j\omega )$就在一些频率上取不到值（衰减因子对不同频率的衰减程度是有区别的），即：
$$F(j\omega ){|}_{\omega ={\omega }_0}{\int }_0^{\infty }f(t)e^{-(\sigma +j{\omega }_0)t}dt>\infty$$
当我们逐渐增大$\sigma$的值，信号衰减幅度不断增大，对应取不到值的频率区间就不断缩小，直到缩小到一个个孤立的点上，就得到了一个临界收敛的状态，若继续增大$\sigma$的值，对应$F(j\omega )$就不再有取不到值的情况，也即原信号衰减后信号满足绝对可积条件。我们把从临界值开始的这个区间$({\sigma }_0,\infty )$视作取值的收敛区间，而$\sigma$作为变量$s$的一部分，$({\sigma }_0,\infty )$被称为$s$的收敛域，在该范围内$\omega$对应$(-\infty ,+\infty )$区域内均有有限取值，讨论信号的频谱也是在这个范围内才有意义。
我们在傅里叶变换的讨论中，通过$F(\omega )\sim \omega$描述信号频谱，为了直观表示出个频率下对应的信号强度变化，我们对频谱取模，使用幅度谱$|F(\omega )|\sim \omega$来描述信号，把幅度谱放在平面直角坐标系中。现在，信号在拉氏变换后得到变量$s=\sigma +j\omega$，在不同$\sigma$取值下有不同的幅度谱，固定后再研究此时对应的幅度谱图像固然是一个比较好的方法，但是，我们不妨在原始幅频分析的平面坐标系上在加一个轴对应$\sigma$的取值，构成三维空间坐标系来表示幅度变化。这样我们不仅可以了解当$\sigma$确定时的幅频变化$F(j\omega ){|}_{\sigma ={\sigma }_0}$，还可以了解$\sigma$取值变化引起的幅频变化的大小。
这里，我们以信号$f(t)=e^t\sin (t)$为例，显然，这个信号不满足绝对可积，对其求拉氏变换，有：
$$\begin{array}{rl}& F(s)={\int }_0^{\infty }{e}^t\sin t{e}^{-st}dt\\ =& {\frac{-\cos t{e}^{(1-s)t}+(1-s)\sin t{e}^{(1-s)t}}{1+(1-s{)}^2}|}_0^{\infty }\end{array}$$
显然有$\sigma >1$，此时：
$$F(s)=\frac{1}{1+(1-s{)}^2}=\frac{1}{[s-(1+j)][s-(1-j)]}$$
收敛域为$\sigma >1$。
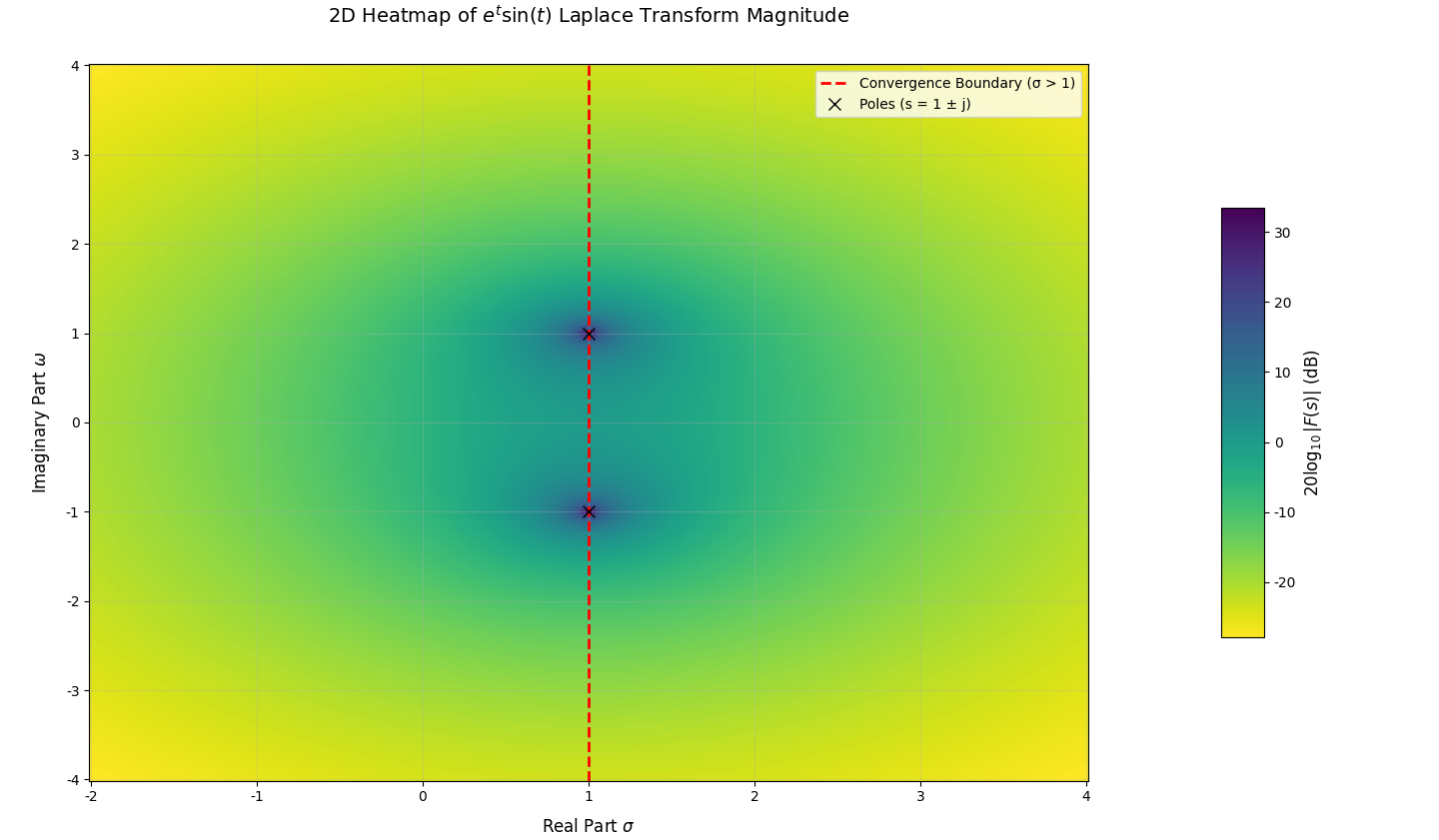
我们据此绘制$|F(s)|\sim \sigma ,\omega$的图像有：

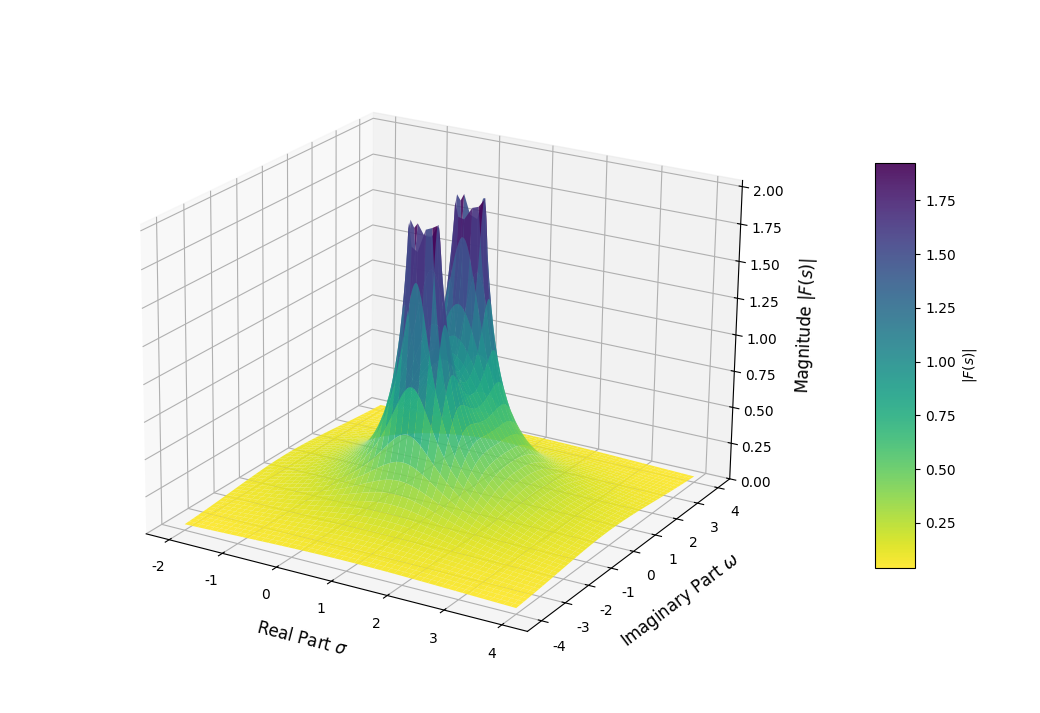
由上面的图像推导过程可知，图像成立的前提是$\sigma >1$，故$\sigma \le 1$部分无实际意义，这部分中信号的拉氏变换不存在。图像所展示的可以认为是函数在该区域的解析延拓。当然，三维图像还是不便展示和观察，我们不妨以$\sigma$和$j\omega$为轴，通过二维热图展示结果，即有：

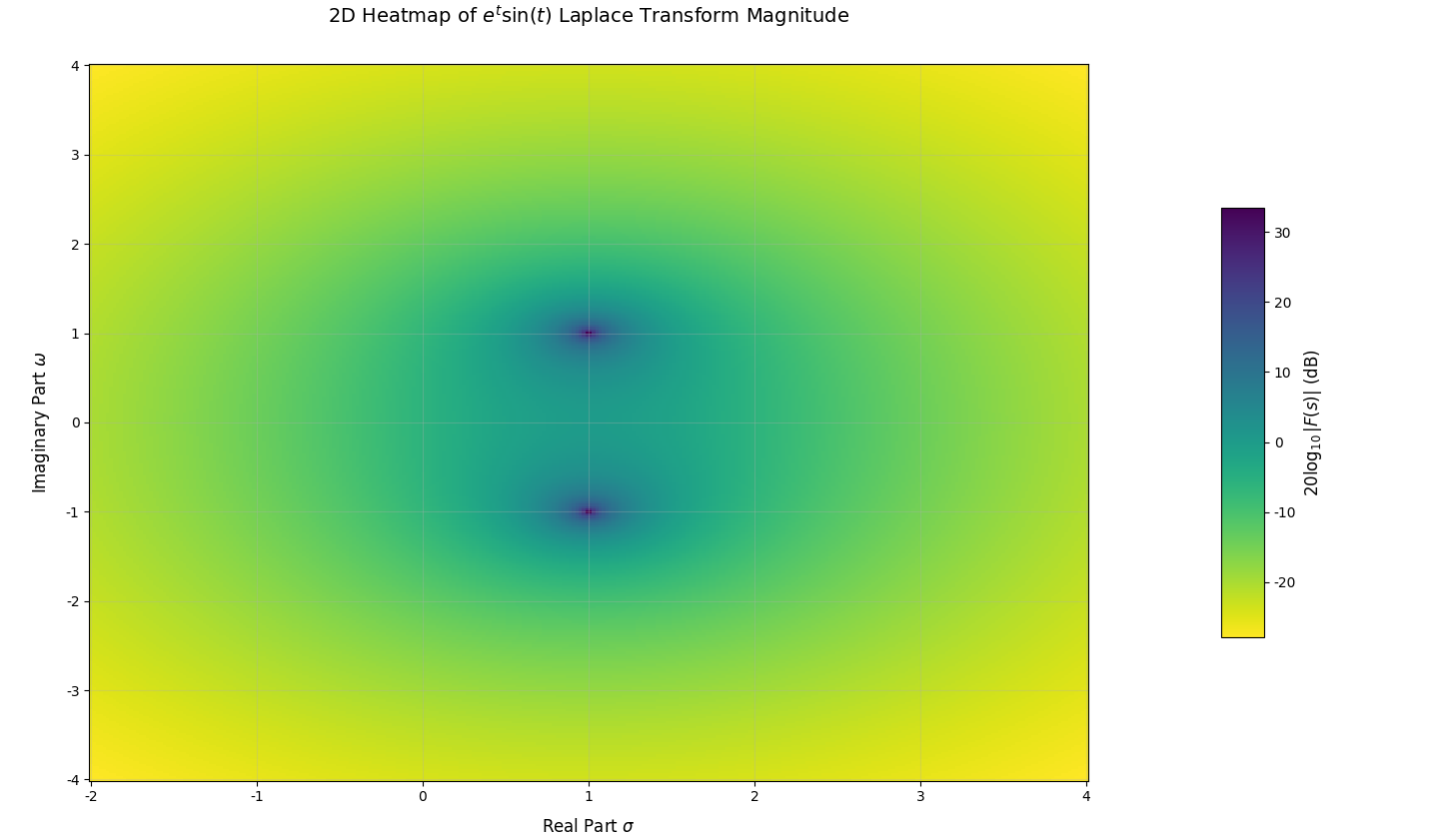
为更清楚地分析图像，我们还需要添加一些小注释。首先，图像只在$\sigma >1$的区域有意义，我们分析的也是这个部分；

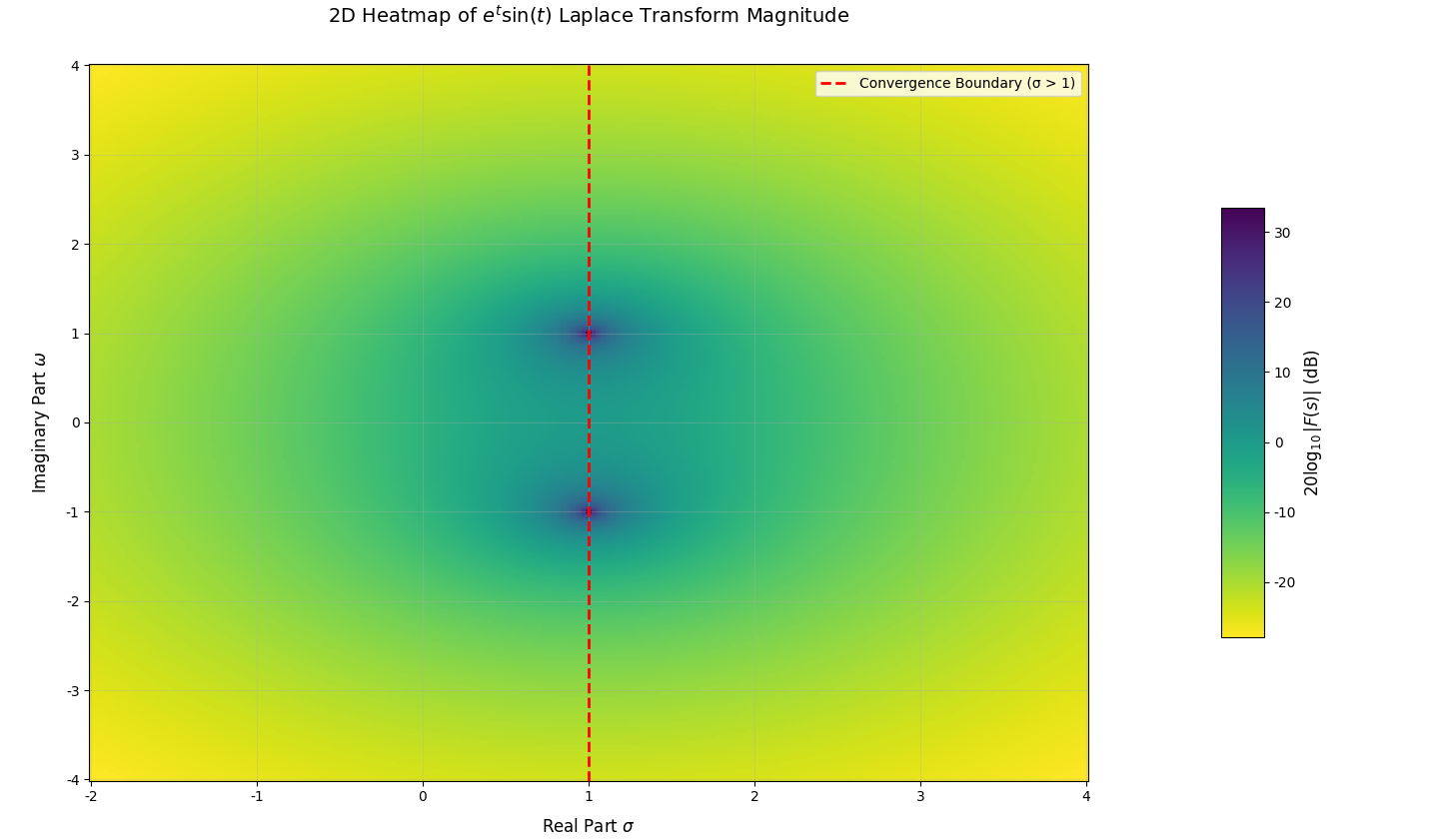
其次，在$\sigma =1$这个临界状态上，信号的拉氏变换仅在$1+j$、$1-j$两个复频率上无定义（趋于$\infty$），这两个点便是信号的极点，图中用$\times$标记表示；

为进一步简化图像，我们可以把热图背景去除，得到：

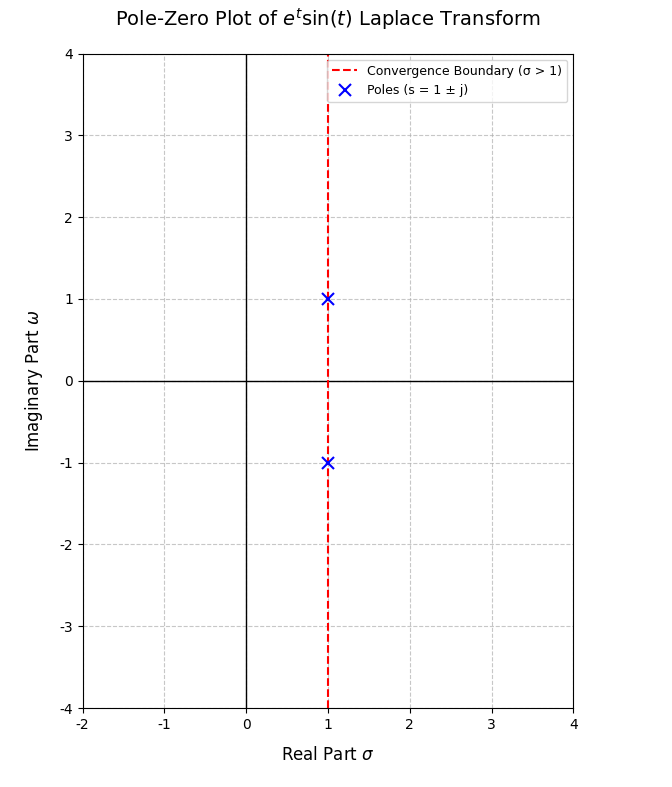
由于极点本就是临界取值，知道了极点，收敛域（$\sigma$边界）自然也就已知了，故可以去除边界线，得到图：

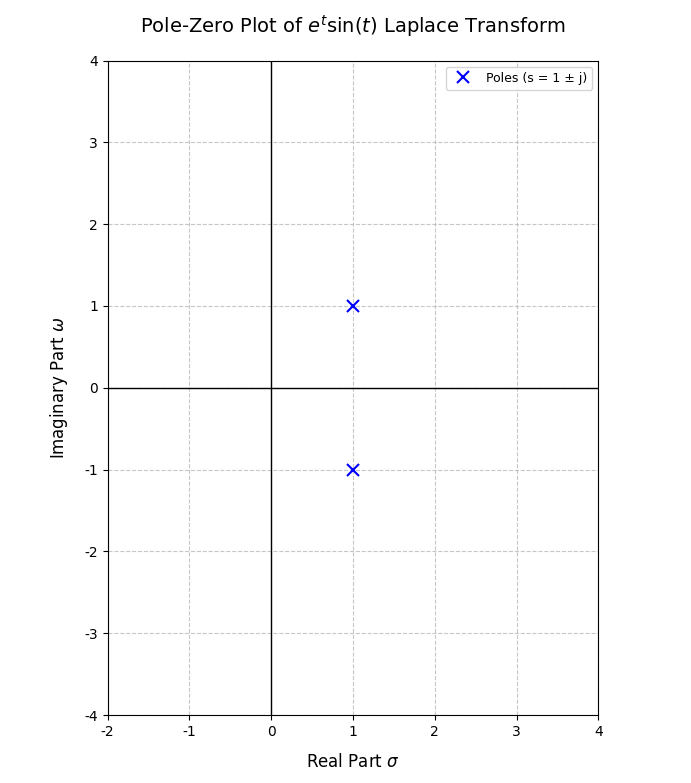
这就是信号的俩是变换的极点图。从图中，我们可以了解到两个信息（极点、收敛域），事实上，这也是拉氏变换最重要的两个信息。此图是基于变量$s$绘制的，基于此图的分析称为$s$域分析。

我们再回头看信号的两个极点$1+j$、$1-j$，对应$\sigma =1,j\omega =\pm j(\omega =\pm 1)$我们把这两个极点连线对应切平面取出：

这是拉氏变换下$\sigma =1$的情况，也可以理解为原信号与$e^{-t}$相乘后的傅里叶变换。注意到这是三角函数$\sin t$的傅里叶变换频谱图像（这里通过幅度谱无法区分是$\sin t$还是$\cos t$，还要看相位谱，这里就省略了），那么，原信号在乘$e^{-t}$后得到$\sin t$，故原信号就是$e^t\sin t$！我们惊奇地发现仅仅通过分析极点便还原了原信号，这就是信号的极点的意义：$s=1\pm j$说明了信号是一个以$e^t$包络的振荡的指数增强信号。
相仿地，我们也可以就其他情况作定性讨论。前面说过，拉氏变换幅度谱是对称分布的，即极点是关于$\sigma$轴对称成对存在的，对于极点$s=\sigma \pm j\omega$，我们可以把对应信号分为以下几类：

1. $\sigma >0,\omega \ne 0$
   此时信号为$e^{\sigma }\sin \omega t$或$e^{\sigma }\cos \omega t$，即信号是一个指数增强的振荡信号。
2. $\sigma =0,\omega \ne 0$
   此时信号为$\sin \omega t$或$\cos \omega t$，信号为等幅振荡的三角信号。
3. $\sigma <0,\omega \ne 0$
   信号为$e^{\sigma }\sin \omega t$或$e^{\sigma }\cos \omega t$，是一个指数衰减的振荡信号。
4. $\sigma >0,\omega =0$
   信号为$e^{\sigma t}$，是一个指数增强信号。
5. $\sigma =0,\omega =0$
   信号为$1$，是一个直流信号。
6. $\sigma <0,\omega =0$
   信号为$e^{\sigma t}$，是一个指数衰减信号。
   下图是上面几种类别的直观表示：
   
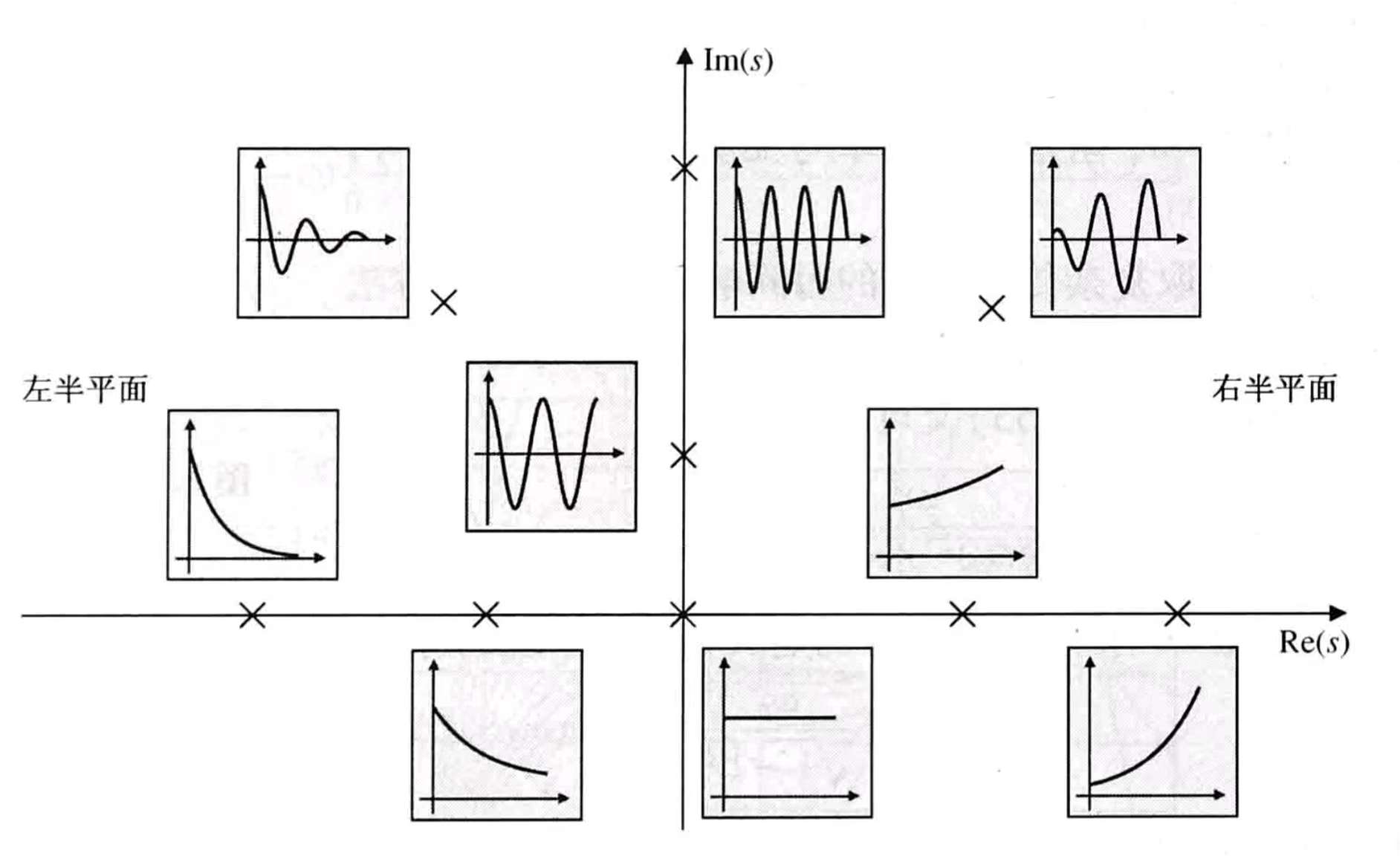
   那么，问题来了，难道信号只有以上几种形状吗？显然不是，这几个信号只是最基本的，体现了信号增强/衰减、振荡/不震荡的趋势，实际信号的增强/衰减与振荡/不震荡可以由多对极点共同决定，同时具体幅度增益由拉氏变换的分子、零点共同决定（本例中分子为1，无零点），这部分不是本文讨论重点，便不再详述。

---

本文主要从傅里叶变换的推广角度介绍了拉氏变换的定义和意义，了解一些常见信号的拉氏变换以及拉氏变换的性质是实际应用中十分必要的，通过拉氏变换的性质也可以了解到前面说的算子法的有效性以及为什么拉氏变换可以化微分方程为代数方程，在后续文章中将进一步介绍常见信号的拉氏变换、拉氏变换的性质、拉氏逆变换的求解以及拉氏变换的重要应用——简化电路分析以及系统分析。