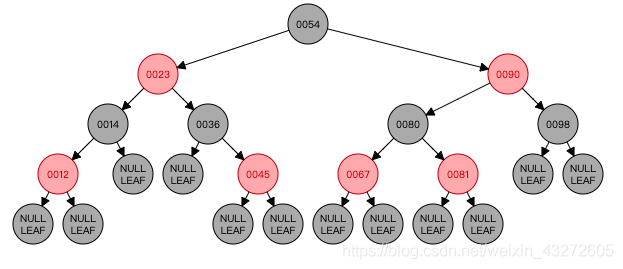
手撕红黑树RedBlackTree Right？带动画的哦

首先这篇博客花了一点时间才总结出来，肯定还有错误，希望各位读者能够小心翼翼的看。尽量理解吧，因为我自己水平也很菜哈哈。还有就是因为看了很多篇博客其实图片都有问题，所以自己就在RedBlackTree上动手实验，然后搞成了gif图片，供大家参考。然后呢，这篇博客是自己看了WiKi后总结的，基本应该没有啥问题，就是稍微做了些改动吧。

首先红黑树是一个二叉查找树，就是加了各种限制，让他成为了一种自平衡的二叉树。首先来看看它的五大特性，这也是我们必须要牢记的，后面多次提到，但我还是会多次重复。

GO🌈黑🌲GO

---

• 树的节点要么是红色的，要么就是黑色的（这是废话，不然怎么叫红黑树）

• 树的根节点一定是黑色的

• 所有的叶子节点一定是黑色的，而且是空的节点。

• 红色节点的两个子节点一定是黑色的，换个方式说，任何两个红色节点都不可能相邻

• 任意一个节点到他所有叶子节点所经过的黑色节点个数一定相同

---

GO🌈黑🌲GO

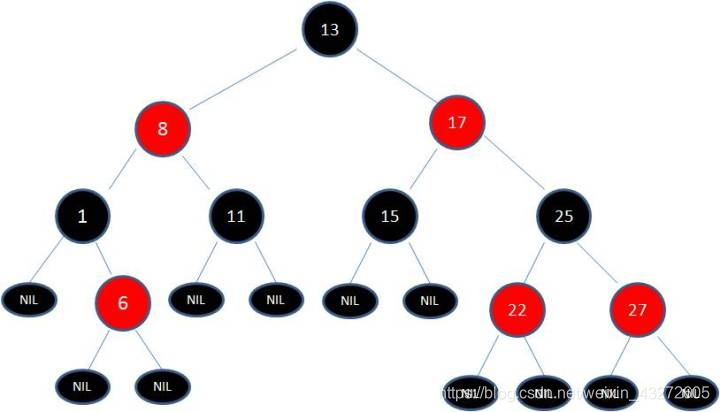
看！！！这就是典型的一个红黑树。注意！！！！！！！ 有些博客很搞，互相抄来抄去，有些错误的图都被抄过去了，百度搜红黑树，10篇文章4篇文章用那个图，注意了，红黑树本身也是二叉查找树，右边的节点一定比左边的大。所以那些右边节点比左边节点小的，或者不满足上面五大特性的图都是错的。我这里这个图是正确的，不用担心。

了解完了红黑树基本性质，现在就要看看它的基操了对吧，所有的东西都要有基操才可以起飞对吧。你准备好了吗！！！

😄红黑树的基操✌️🐂👃

变色

变色很简单，我们刚插入的节点一定是红色的

注意！！！再强调一遍，为了插入的节点尽量少影响红黑树的性质，一定是刚插入的节点填充为红色。不信你先复习一下五大特性：

---

• 树的节点要么是红色的，要么就是黑色的（这是废话，不然怎么叫红黑树）

• 树的根节点一定是黑色的

• 所有的叶子节点一定是黑色的，而且是空的节点。

• 红色节点的两个子节点一定是黑色的，换个方式说，任何两个红色节点都不可能相邻

• 任意一个节点到他所有叶子节点所经过的黑色节点个数一定相同

如果填充为黑色：不会违背特性1，2，3对吧，都是废话。虽然没有违背特性4，但是呢那还要红色节点有什么用呢，因为只说红色节点不能相邻，有没有说黑色节点不能相邻，那么这样就退化成了二叉查找树了。特性5就更可能违背了。

如果填充为红色：特性1，2，3，5都不会违背，只要看特性4，而且很适合红黑树的性质。

记住了，所谓变色就是红变成黑，黑变成红。好像是废话。那不看了吧。

---

左旋

看好上图了，哥哥姐姐们😄，这就是左旋，用你的余光看它，他就是在往左边转。 具体的就是：我们以待旋转的节点(E节点)为中心，将它的右节点(S节点)的左子树，变成自己的右子树，并且之前的右子树成为自己的父节点。

---

右旋

看这个图也很明显了吧，用你的余光去看，它整体就是往右边转的。具体就是：以待旋转的点(S节点)，整体向右旋转，将左节点(E节点)的右子树变成自己的左子树，并且原来的左节点(E节点)变成自己的父节点。

---

你可以休息一下，因为等下会用到上面所有的东西，很复杂！！！！！

---

😷😄🐂🐶🐱🎩🐸红黑树的插入和删除😷😄🐂🐶🐱🎩🐸

---

插入

我们之前说过了，刚插入的节点一定是红色的。那么就会根据上面的五大特性，一旦违背了某一个特性，就要用一些基操来弥补。

1⃣️：插入的节点是根节点，那么不要任何左旋右旋，就是变色，将其变成黑色即可。

2⃣️：插入的节点的父节点刚好是黑色，这时候就不需要变色，因为不违背任何一条特性。

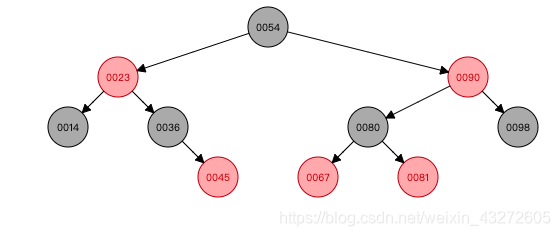
当我插入12

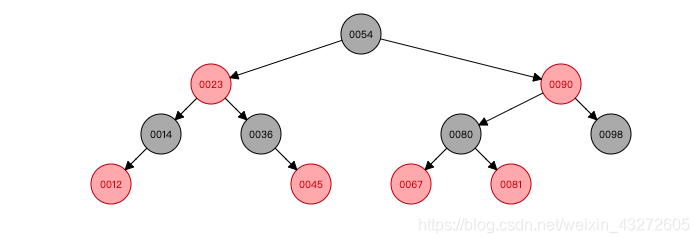
3⃣️：但是插入的节点父节点是红色的话，就要又要分几种情况了。但是总的原理就是要把红色节点一直弄到根结点再把根结点弄成黑色，当然，半路可能遇到了连续的黑节点，当把一个节点弄成红色了，就不会有连续的红色节点了。不用担心，等会儿去看看。首先看看不同情况：

叔叔节点：即父亲节点的兄弟节点，例如上面14和38就是兄弟节点，12的叔叔节点是38.

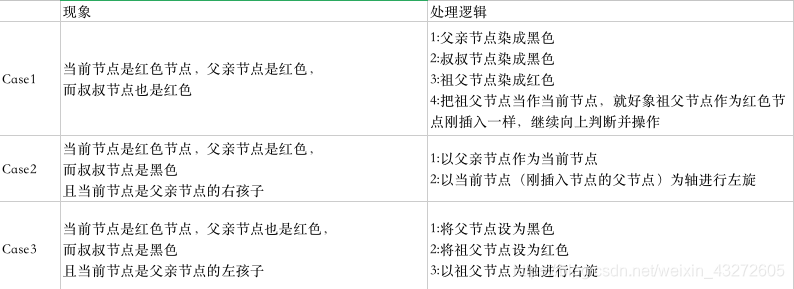
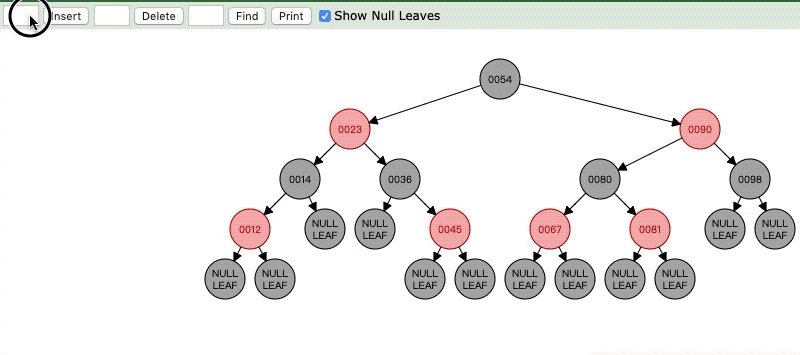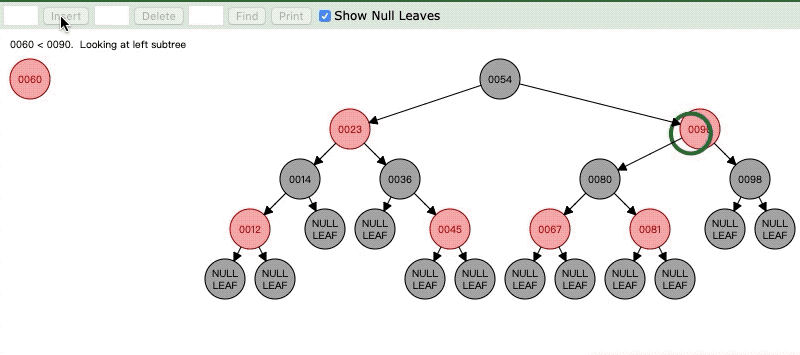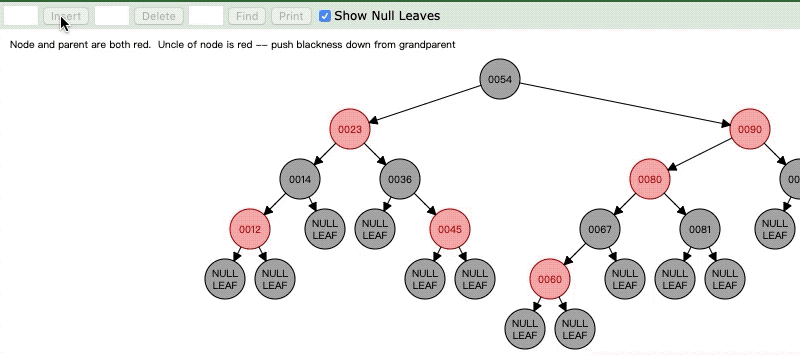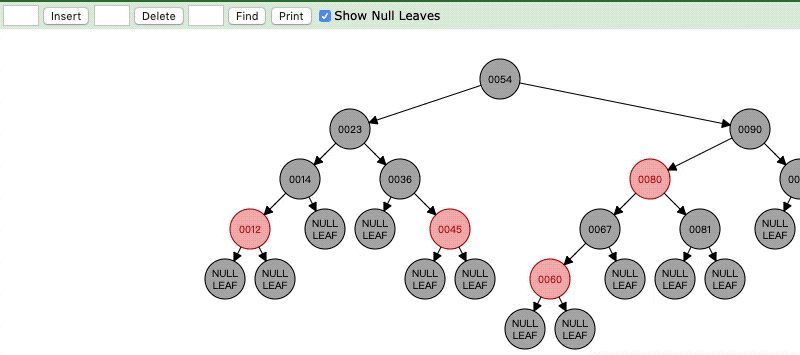
Case1:父亲节点是红色，而且叔叔节点也是红色

这个时候就是将父亲节点设置成黑色，叔叔节点设置成黑色，祖父节点设置成红色，然后以祖父节点为当前节点，继续向上操作（感觉就像变成祖父节点刚插入一样）。

原因：首先，我们要知道，如果父亲节点也是红色节点，那么在我们插入新节点之前，这棵红黑树是已经平衡好的了，所以既然父亲节点是红色，那么祖父节点一定是黑色(因为两个红色节点不能连续)。然后当我们插入红色节点，将父亲节点染成黑色，但是这时候对祖父节点来说，它由父亲这边就会比叔叔节点那边多一个黑色节点，所以我们不得不把叔叔也变成黑色。那么为什么又要将祖父节点变成红色呢。其实道理是一样的，因为父节点和叔叔节点变成了黑色，那么对于祖父节点的父节点来说，祖父节点这边的黑色节点会比祖父节点的兄弟节点的黑色节点要多，所以我们必须把祖父节点变成红色来抵消掉叔叔和父亲节点的颜色变化。。有人又有疑问，明明是两个节点变成黑色，为什么只有祖父节点一个节点变成红色？注意了，是任意一个节点到自己叶子节点路径经过的黑色节点相同，所以对祖父节点的父亲节点来说，它经过祖父节点->父节点，和祖父节点->叔叔节点是两种不同路径，他们经历的黑色节点是一样的。

当我插入60

Case2:父亲节点是红色，但是叔叔节点是黑色，而且当前节点是父亲节点的右孩子

这个时候是先将父亲节点作为当前节点，然后以当前节点为轴进行左旋。注意，左旋之后可能会出现Case3，所以两个case可以串起来看，相应的，case3后也可能出现case2。大家凑合着看。

原因：一般来说，我们一切的左旋右旋都是为了将插入的红色节点上浮一直到根结点，或者中途有连续的黑节点阻拦。但是呢，我们可以仔细看看这种情况，一旦当前节点是红色，父亲节点黑色，叔叔节点黑色，当进行左旋之后，是不是原来的当前节点变成了现在父节点，原来的父节点变成了现在的当前节点了。（注意这里当前节点已经变了，不要还在想之前的当前节点了），这时候就是Case3的情况了，所以应该又要根据Case3进行操作了。
首先看看Case2

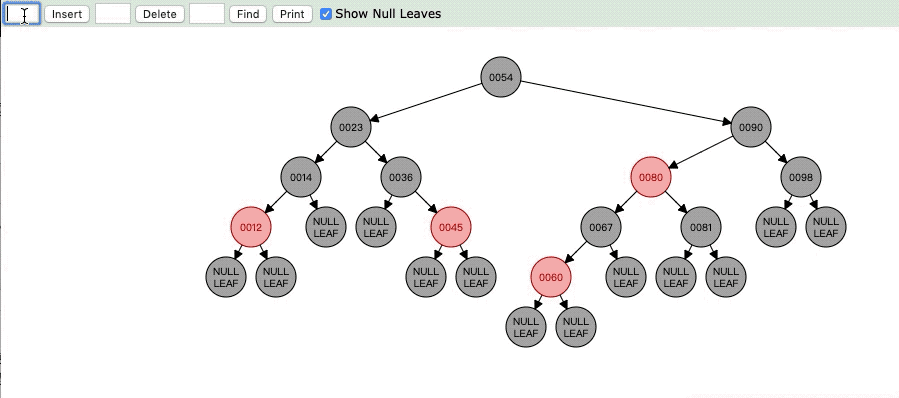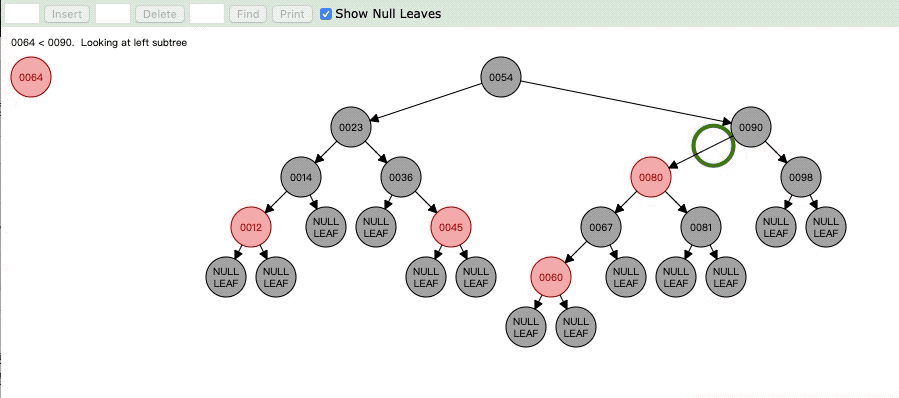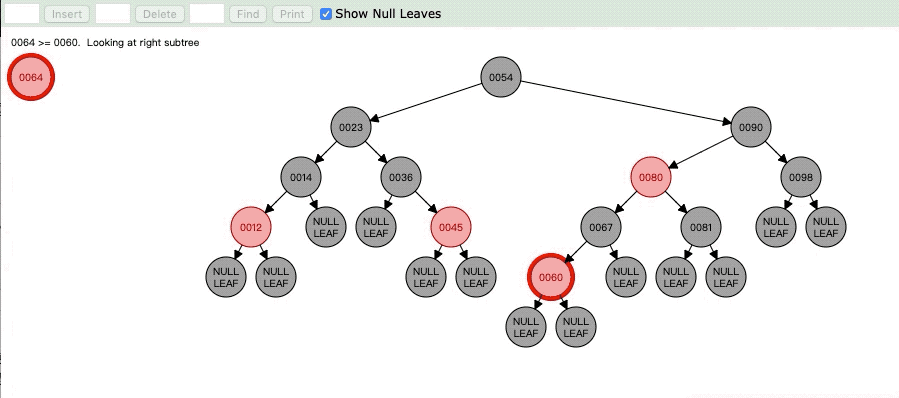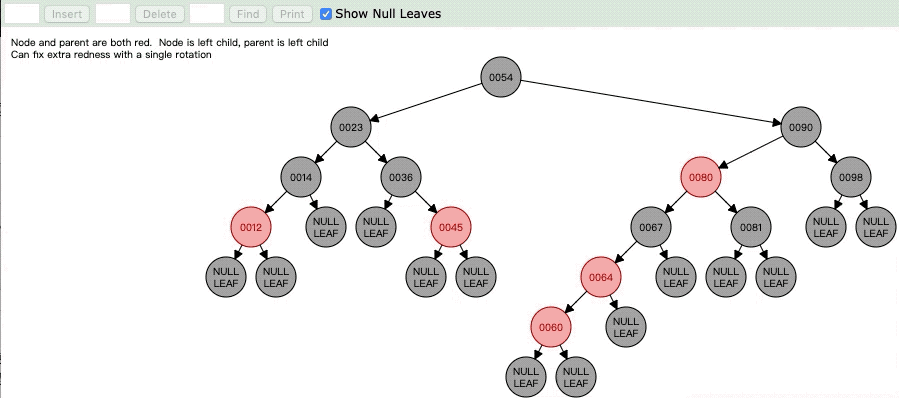
看清楚最后了吗，左旋之后，一共两个红色点连在一起了，对不对。这样子

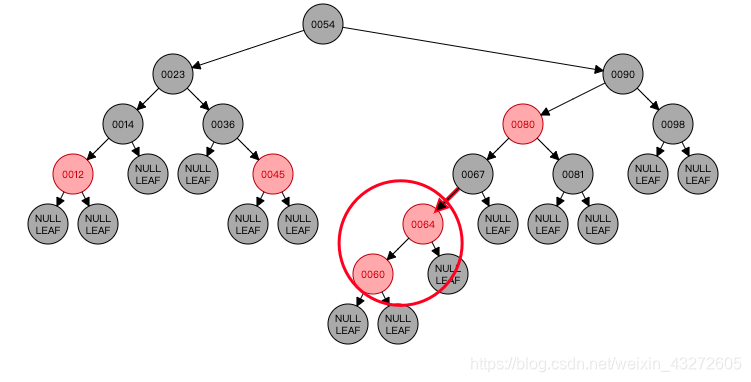
此时的当前节点是60，对不对？有人有疑问了，为啥当前节点是60，自己看清楚上面的Case2的处理逻辑，我们说好了先将当前节点变成父节点，然后以父亲节点进行左旋，所以左旋之后当前节点应该是60(60是原来的父节点对吧)。

如果你理清了当前节点是60的话，那么我们在来看现在的情况，就是说60是红色，它的父亲节点64是红色，而叔叔节点是Nil也就是黑色节点，那么很明显就满足了Case3，那么我们就来看看Case3

Case3:当前节点是红色节点，父亲节点也是红色，但是叔叔节点是黑色节点，这时候要将父亲节点设为黑色，然后将祖父节点设为红色，并且以祖父节点为轴进行右旋

原因：我们遇到了种种情况，是要把父节点染成黑色的，但是对于祖父节点来说，父节点这边就多了一个黑色节点，又因为叔叔节点本身就是黑色的，无法像Case1一样染黑和父节点平衡。只能通过将祖父节点染成红色，然后以祖父节点为轴右旋，就如下面的gif图像所示。

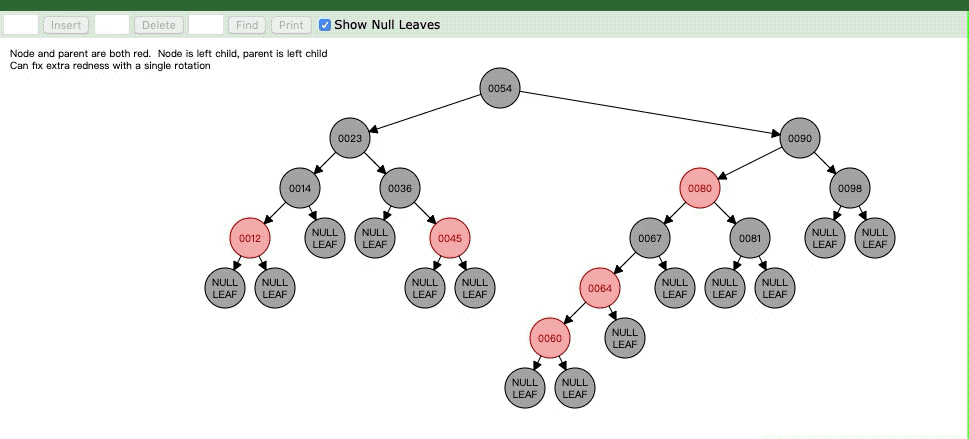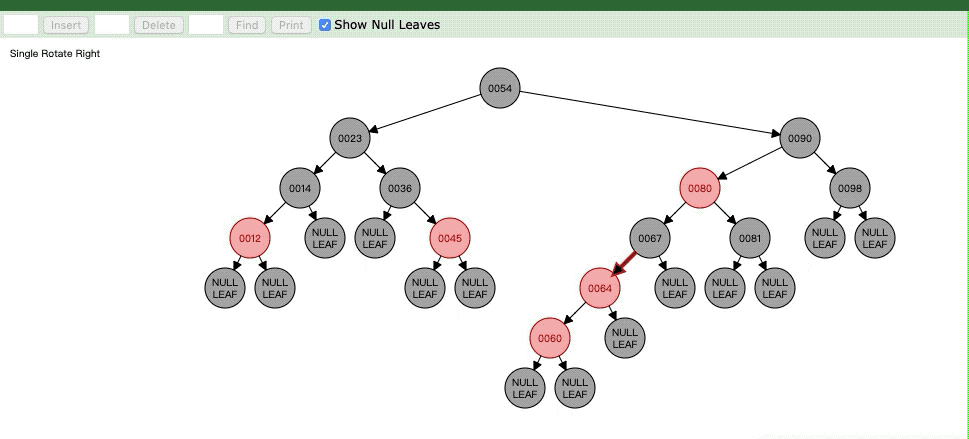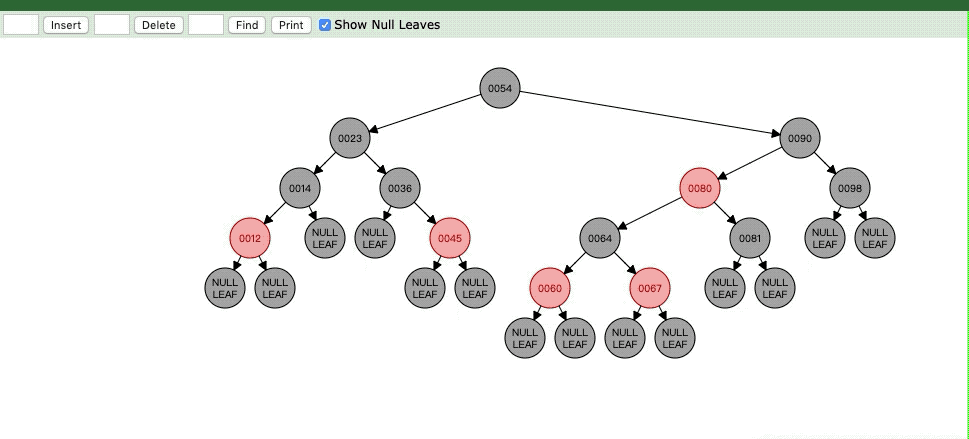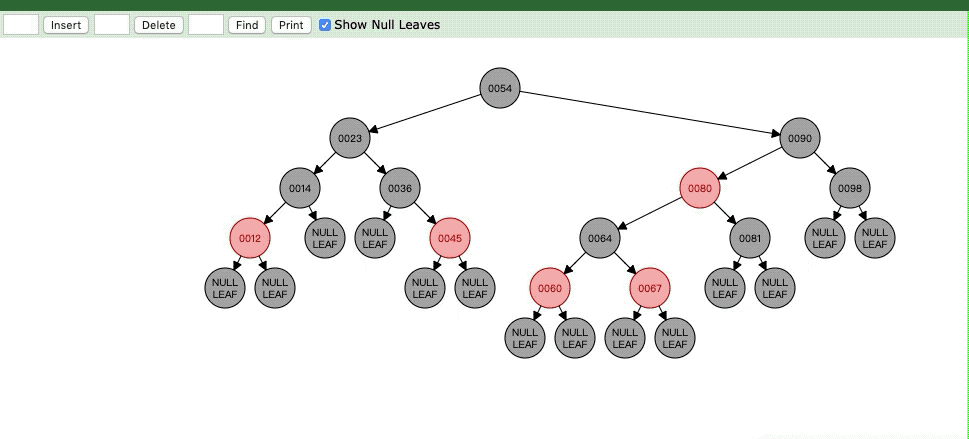
最终是不是这个样子

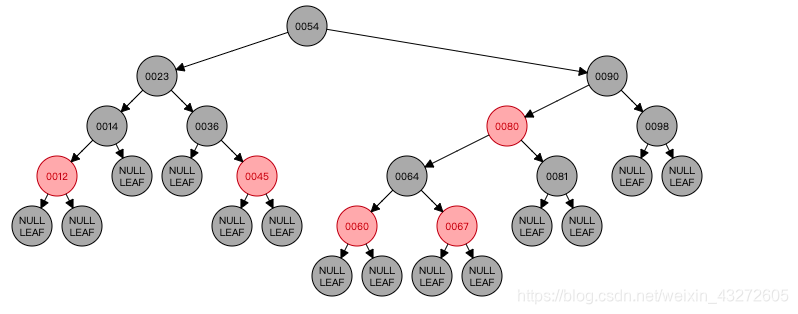
以上就是红黑树的插入，注意了，一定要弄清楚当前节点是什么，理论上你可以把当前节点看作一个插入节点来看的，因为它一般是红的。不过还是按照上面的Case比较好。只要你掌握当前节点，然后以当前节点判断上面三种情况，自下而上不断操作，最后就会颜色平衡，其树的高度也能够自平衡。

好了，👍暂且可以休息一下♨️，因为我们才把红黑树的插入搞完，还有删除呢。之后还要实现代码。如果你休息完了直接开始把

红黑树的删除

删除节点和普通的查找二叉树差不多，删除过程是一样的，只是后来多了一个自平衡的过程。不要担心，体谅体谅吧。复习一下删除节点过程：

• 1⃣️如果这个要删除的节点是最后一个节点，也就是叶子节点，但是在红黑树里面叶子节点是NIL的空节点，这里就理解成子节点是NIL的节点吧。这种情况下直接删除即可。
• 2⃣️如果要删除的节点有一个子节点，那么直接用子节点替代掉自己就行。
• 3⃣️这个就比较巧妙了，前面的情况要么是没儿子，要么只有一个儿子，那现在就是有两个儿子的情况了，这时候就是先找到带删除节点的后继节点(后继节点就是比当前大的下一个节点，注意这里并不一定是子节点。像下面这个图54的后继节点就是60。懂了吧)。找到之后，将后继节点的内容替代掉待删除节点的内容，然后我们就要删除后继节点。这个后继节点有个特点，它一定是某个节点的左节点，这是查找树的特质，因为左子节点一定比自己小。正因为这样，我们找54的后继节点就一定是在它的右子树找，然后一直往右子树的左节点找，最终的那个左节点才是后继节点。那么后继节点是肯定没有左节点的，可能有右节点，所以我们复制完后继节点后，就要将后继节点删除，这时候根据儿子的数量就去情况1⃣️或2⃣️
  

删除后的自平衡

不管怎么样，总不能违背那五个特性，所以我们需要通过旋转，变色来维持那五个特性。

---

• 树的节点要么是红色的，要么就是黑色的（这是废话，不然怎么叫红黑树）

• 树的根节点一定是黑色的

• 所有的叶子节点一定是黑色的，而且是空的节点。

• 红色节点的两个子节点一定是黑色的，换个方式说，任何两个红色节点都不可能相邻

• 任意一个节点到他所有叶子节点所经过的黑色节点个数一定相同

---

前面说了，要删除一个节点，如果有一个孩子或者没有孩子，可以直接拿孩子节点替代对吧。但是如果有两个孩子的话，找到这个节点的后继节点，颜色还是不变，只是把后继节点的内容复制过来就行，这样就不会影响颜色，然后转而去删除后继节点，这样后继节点也只有一个孩子或者没有孩子，从而可以将整个问题转变成删除一个最多只有一个孩子的节点。这里一定要弄清楚！！！！弄清楚再往后看。

那么就开始进入真正的删除过程。这个真正的删除过程的删除的节点是最多只有一个孩子的节点！！还是再强调，整个问题已经转成了删除最多只有一个孩子的节点。OK。如果删除的节点是红色，我们直接拿孩子节点补上就行，但是如果删除的是黑色，那就麻烦了。

但是不管怎么样，我们直接将删除节点用它的孩子替换掉，并将替换之后的节点作为N，删除节点的父节点也就是替换节点N的父节点作为P，而删除节点的兄弟节点也就是替换节点N的兄弟节点作为B，且兄弟节点的左节点为BL，右节点为BR。！！！！！！！而且注意了，下面情况中都没有删除节点的表示了，只有替换节点N！！！！

那么我们就要分别去区分不同的情况了，各位老板们。

Case1

• 如果删除的节点是红色的，那么我们可以直接将孩子节点N补位，因为孩子节点一定是黑色的，并没有影响任何五大特性。

这种情况不要说了吧，很明显应该没有问题，红色节点一定只有黑色孩子，这里因为找不到黑色非空孩子节点的情况，就将NIL叶子节点当作黑色节点吧，这也是算法导论里面为了让算法表达更容易从而加入NIL黑色空节点的原因。可以看到整个没有影响到平衡的。

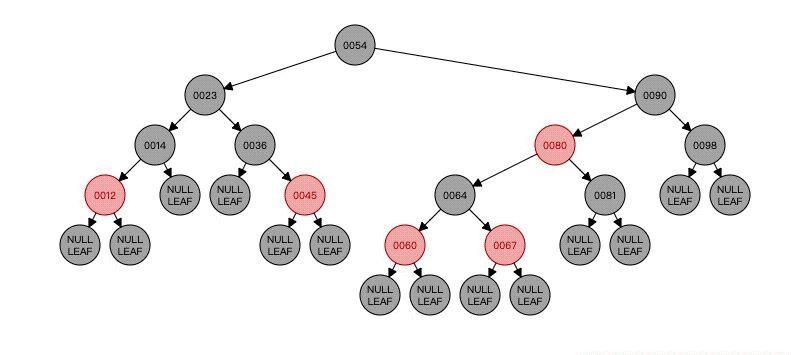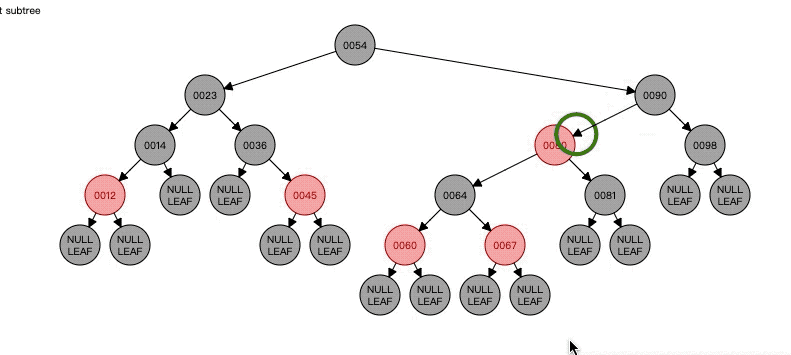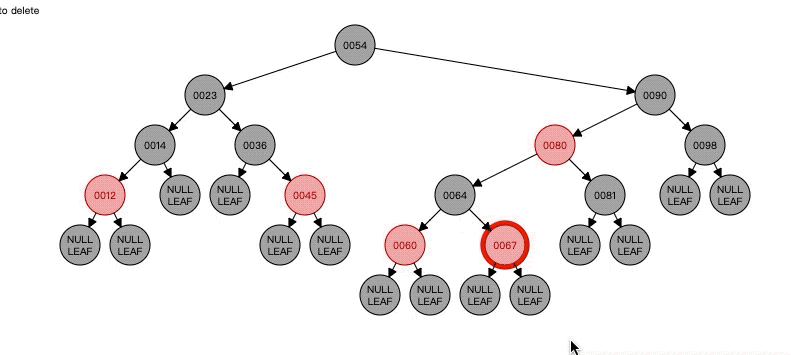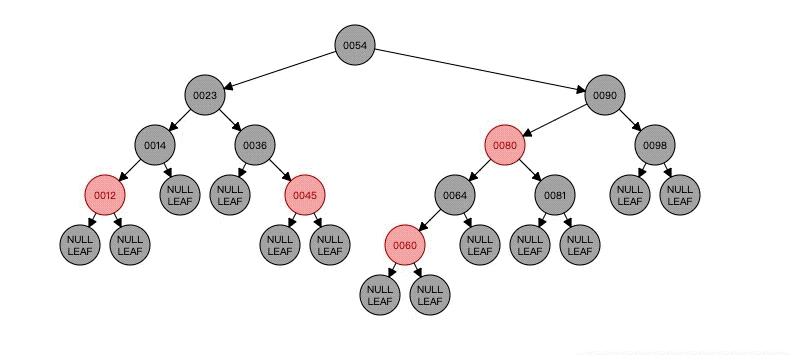
Case2

• 如果删除节点是黑色，且它的孩子是红色，那么直接拿红色孩子替换删除节点就行了。并且把孩子节点染成黑色。

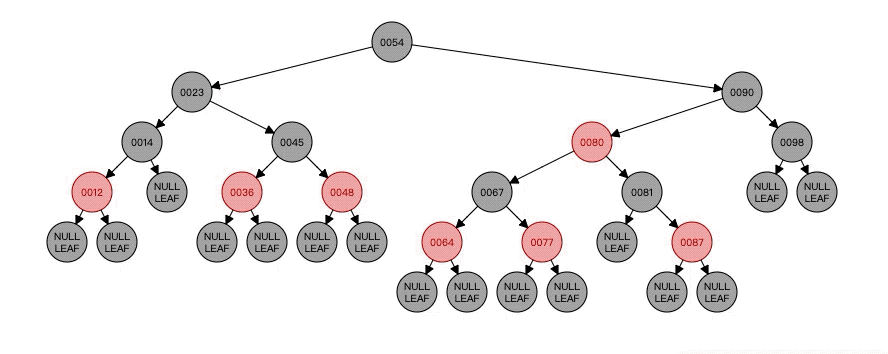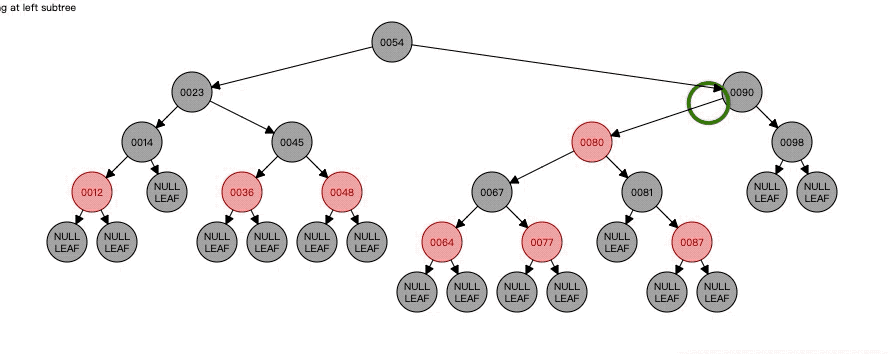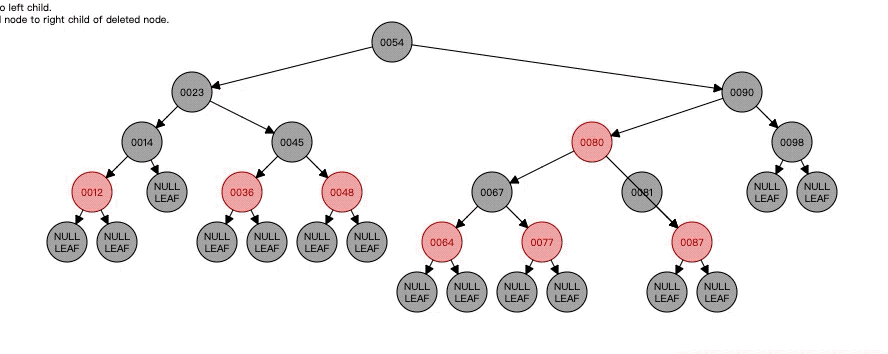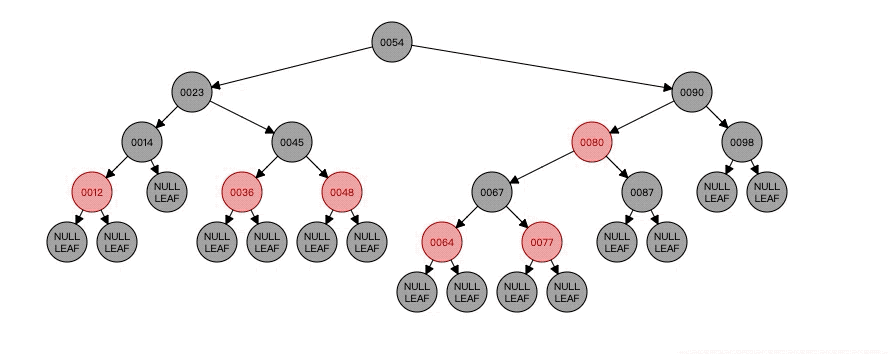
以上两种情况都还好的，下面就是黑色删除节点+黑色N的各种情况了。而且下面的情况更为复杂，因为涉及到左旋右旋，所以下面情况可能是以删除节点作为其父节点的左孩子所做的操作，如果作为有孩子的操作就会相反。

Case3

• 替换节点N是左节点：如果删除的节点是黑色，而删除的孩子节点N也是黑色。父节点P也是黑色，但是兄弟节点B是红色，兄弟节点的孩子BR和BL是黑色节点。那么这种情况就是当孩子节点N替代掉删除节点后，先将父亲节点P变为红色，然后将兄弟节点B变为黑色，再以父亲节点P为轴进行左旋。

• 替换节点N是右节点：如果删除的节点是黑色，而删除节点孩子N也是黑色。父节点P也是黑色，但是兄弟节点B是红色，兄弟节点的孩子BR和BL是黑色节点。那么这种情况就是当孩子节点N替代掉删除节点后，先将父亲接待你变成红色，然后兄弟节点B变成黑色，再以父亲节点P为轴进行右旋。

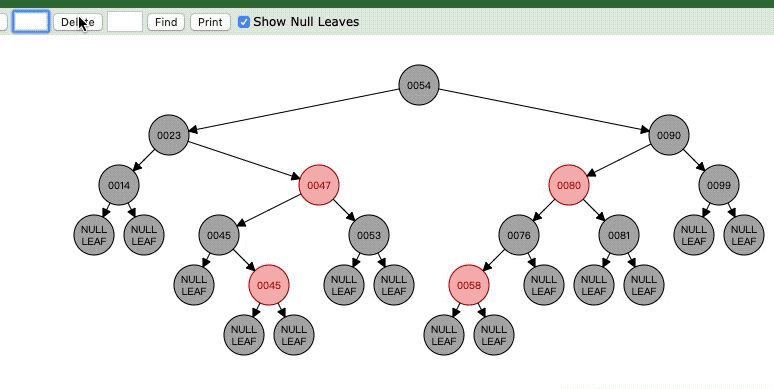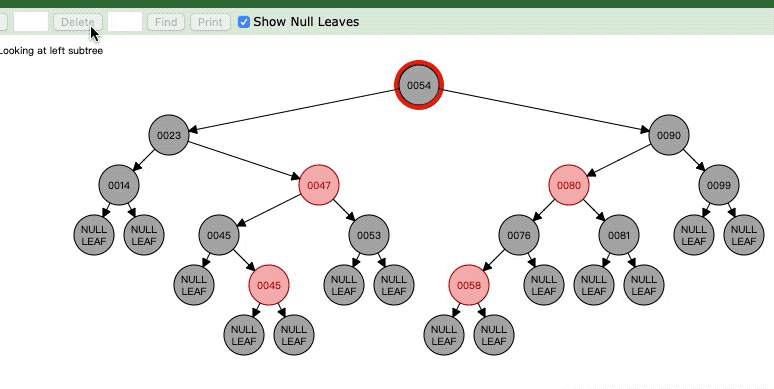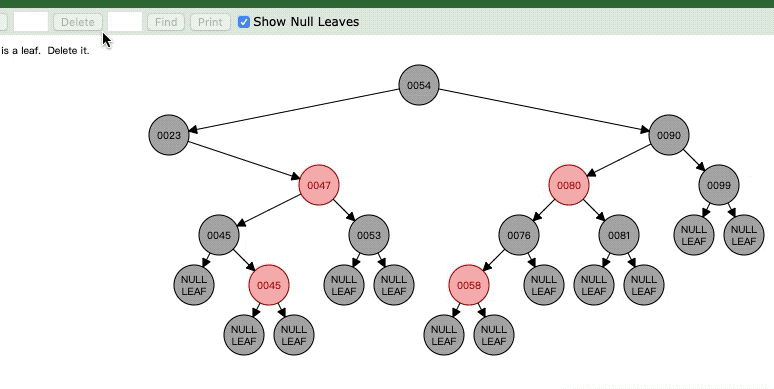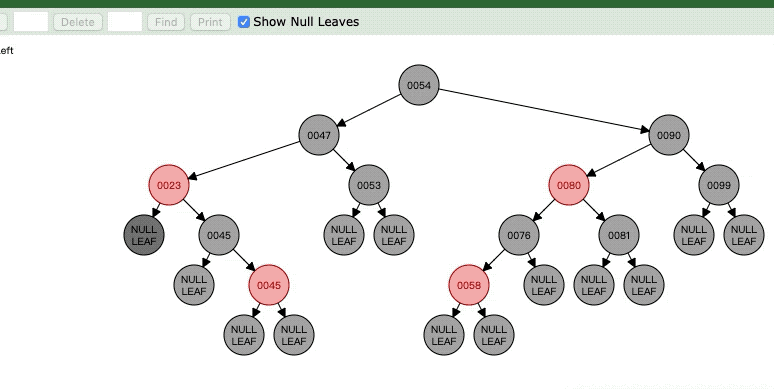
这里对于节点14，它的父节点23是黑色的，它的兄弟节点是红色的，这时候操作就是将14删除后，它的子节点或者空节点成为23的子节点，然后父亲节点变成红色，兄弟节点47变成黑色，最后以父亲节点23为中心进行左旋。

注意一下，与14相同的还有最右边的99，只是14是作为23的做孩子，99作为90的右孩子，所以对99来说，旋转操作是右旋！！注意了，上图是作为左孩子才是左旋，如果是右孩子就是右旋。

然后看看最后状态图，现在的N是23的左节点NULL LEAF空节点，那么可以看见23的左右节点明显不平衡对吧，黑色节点多了。所以这时候就要看Case4了。

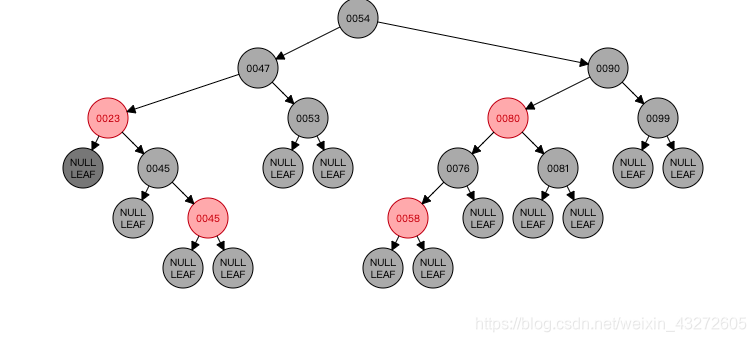
Case4

• 如果当前节点作为左孩子，如果当前节点N是黑色，父节点颜色无所谓，兄弟节点B是黑色，兄弟节点的右孩子BR是红色，兄弟节点的左孩子BR无所谓，那么这时候就要将当前节点N的父亲节点P的颜色给兄弟节点B，然后将父节点设为黑色，将N兄弟节点的右子节点设为黑色，之后以N的父节点P为轴进行左旋。

• 如果当前节点作为右孩子，如果当前节点N是黑色，父节点颜色无所谓，兄弟节点B是黑色，兄弟节点的左孩子BL是红色，兄弟节点的右孩子BR无所谓，那么这时候就要将当前节点N的父亲节点P的颜色给兄弟节点B，然后将父节点设为给色，将N兄弟节点的左节点BL设为黑色，之后以N的父节点P为轴进行右旋。

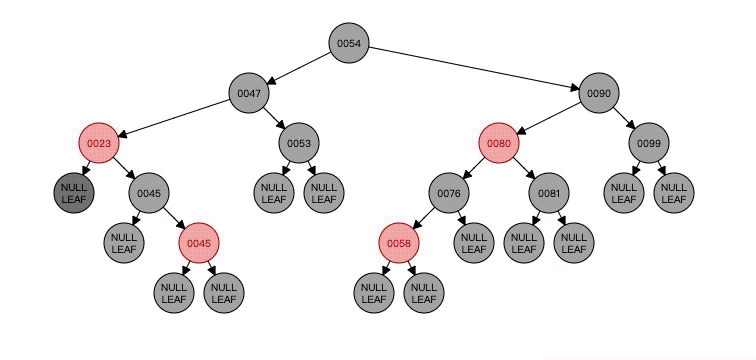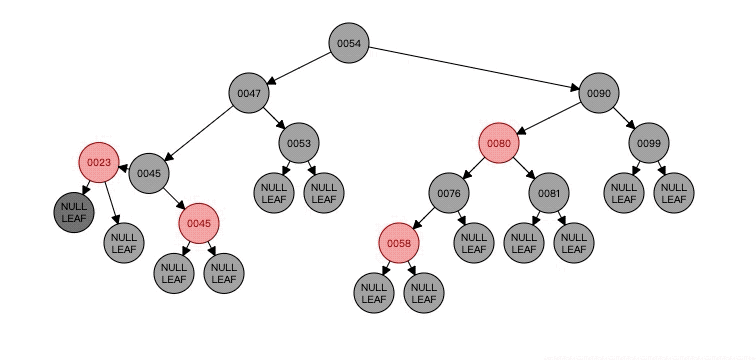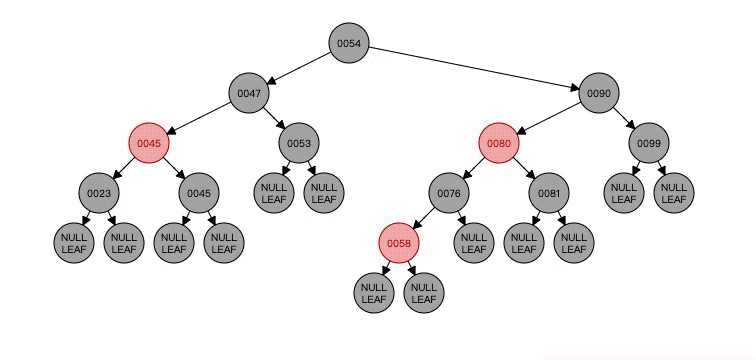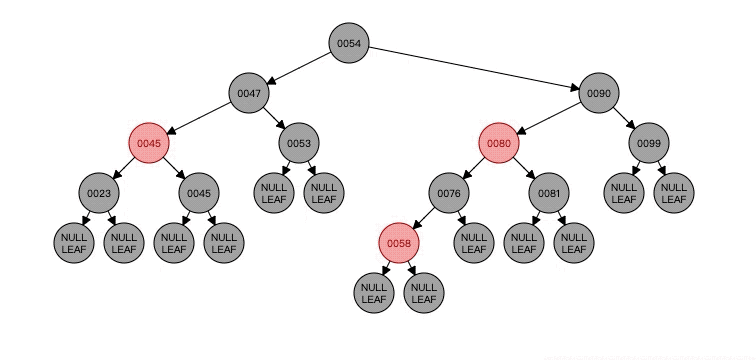
看看这个，可以看到N(NULL LEAF)的父节点P(23)的颜色红色给了N的兄弟节点B(45)，然后父节点P(23)变成了红色，之后兄弟节点B的右孩子BR(45)变成黑色，最后将以父节点P(23)为轴进行了左旋。

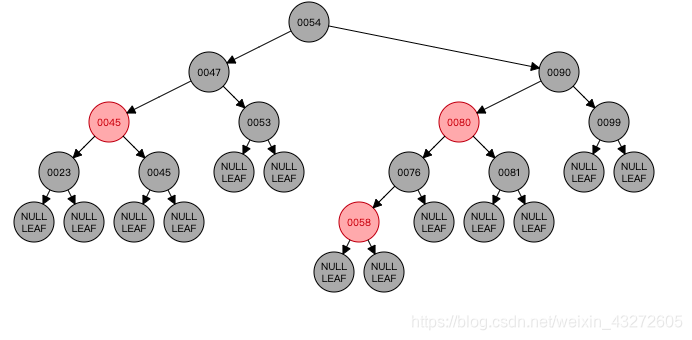
Case5

• 如果N节点作为左孩子，如果N节点也是黑色，那么如果N的兄弟节点B是黑色，而且兄弟节点的两个孩子也是黑色的，而且父亲节点是红色的，那么直接将兄弟节点B和父亲节点颜色互换就行。

• 如果N节点作为右孩子，如果N节点也是黑色，那么如果N的兄弟节点B是黑色，而且兄弟节点的两个孩子也是黑色的，而且父亲节点是红色的，那么直接将兄弟节点B和父亲节点颜色互换就行。

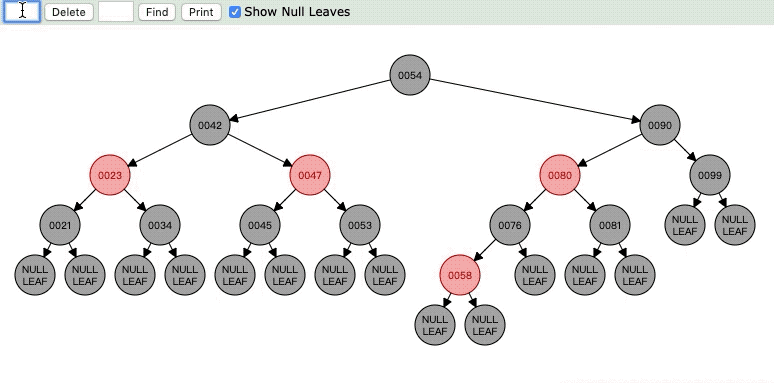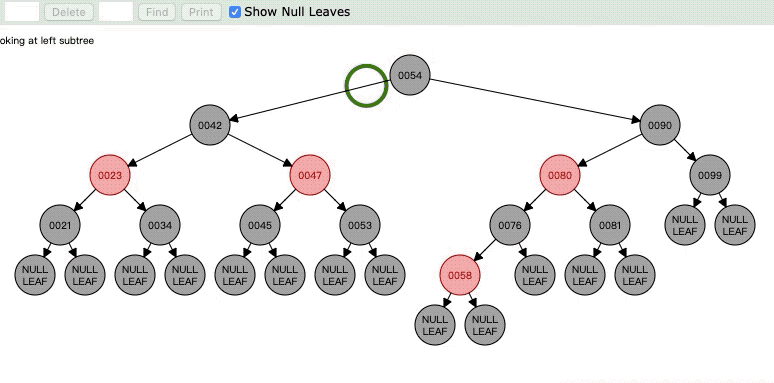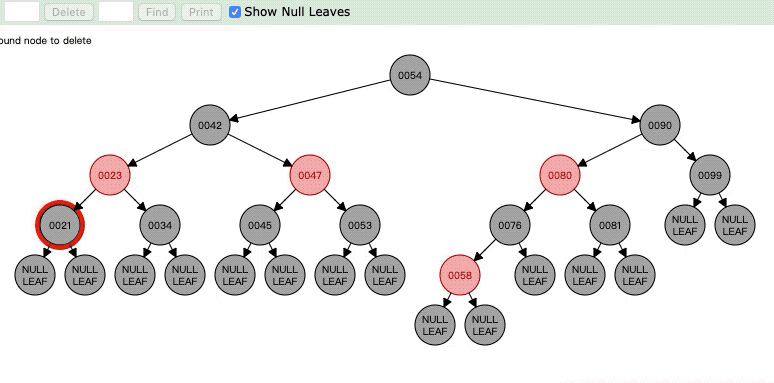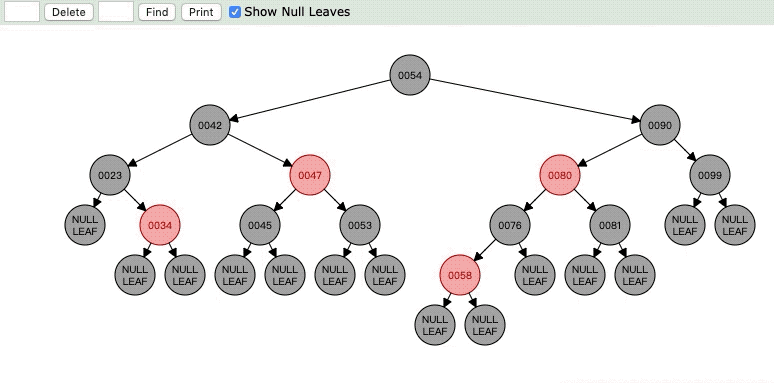
为什么互换就可以了，我们想一想，我们删除了21，是不是23->21->NULL 这条路就少了一个黑色节点，但是23->34->NULL却没有问题，这时候将兄弟节点和父亲节点颜色互换就OK了。前提是兄弟节点的两个子节点也是黑色的。

Case6：官方的可能没有这种情况，但是我还是列举出来，因为和Case5其实差不多去。

• 这个就是N节点的兄弟节点是黑色，两个子节点也是黑色的，但是父亲节点是黑色的。这种情况下只能将兄弟节点变为红色，这样两边黑色节点个数就相同了。N节点作为左孩子右孩子无所谓

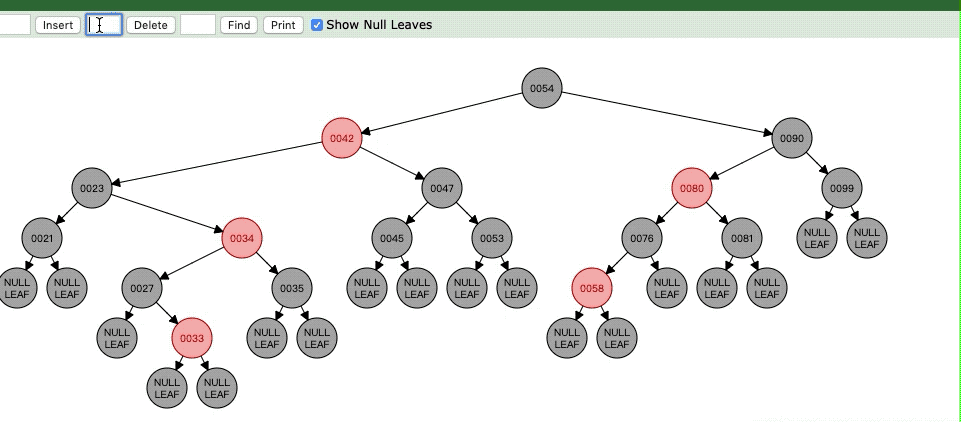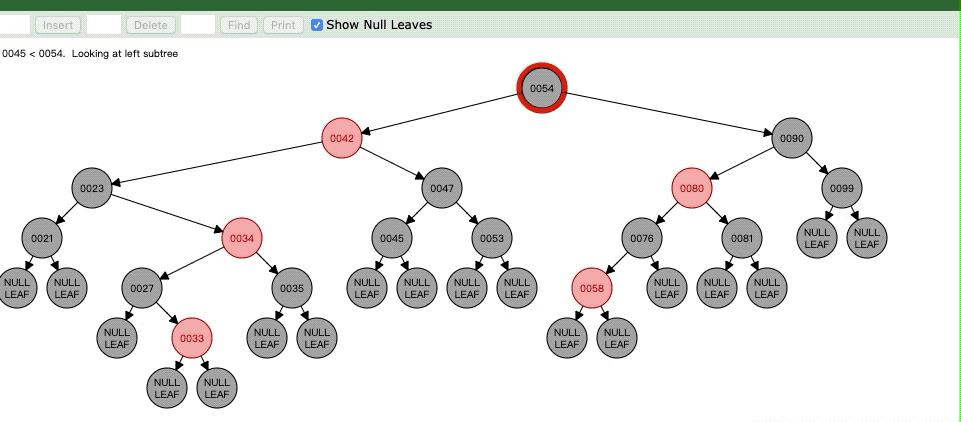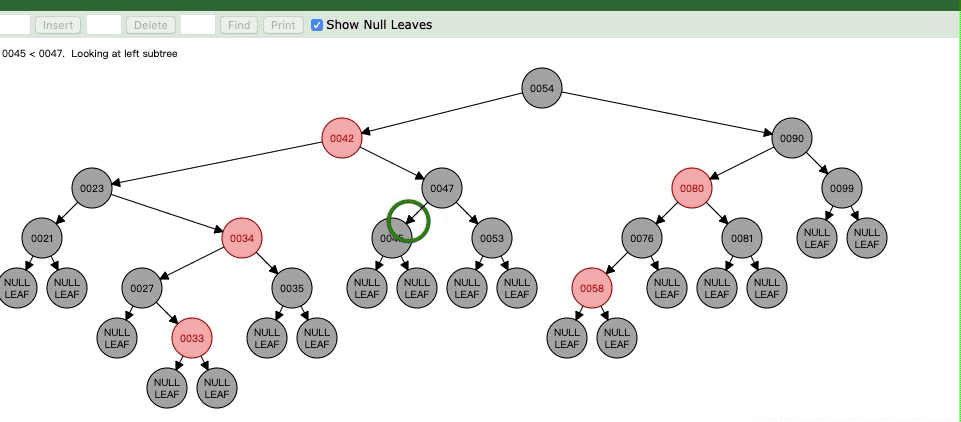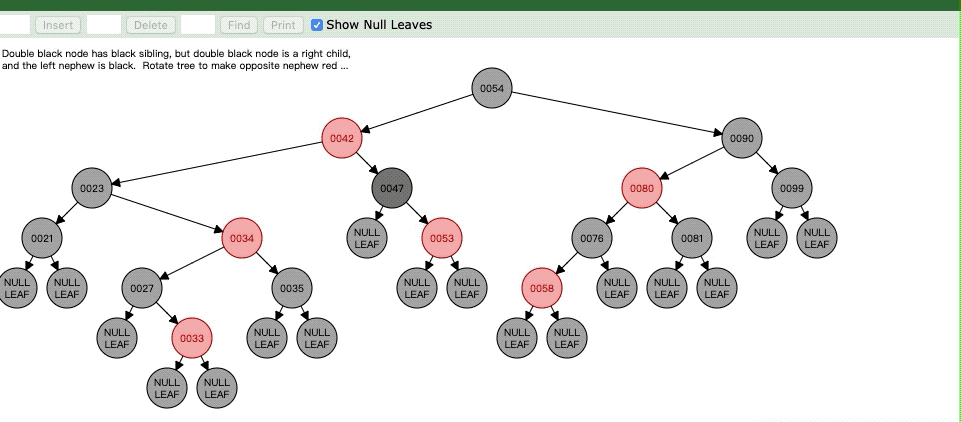
但是呢，虽说这样但是42->47还有42->23的黑色点明显就不同了，明显就少了一个，所以现在要对47进行平衡，也就是令47为N了，接下来就看Case7

Case7

如果N是黑色左节点：那么不管父亲节点是什么颜色，如果兄弟节点B是黑色的，且兄弟节点B的左节点BL是红色，右节点BR是黑色，那么就以B为轴进行右旋操作，然后互换B和BL的颜色。

如果N是黑色右节点：那么不管父亲节点什么颜色，如果兄弟节点B是黑色的，而且兄弟节点的右节点BR是红色，左节点BL是黑色，那么就以B为轴进行左旋操作，然后互换B和BR的颜色

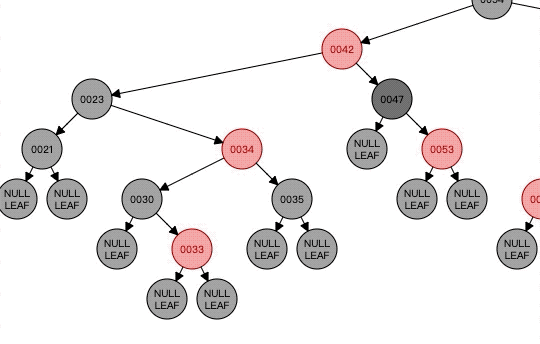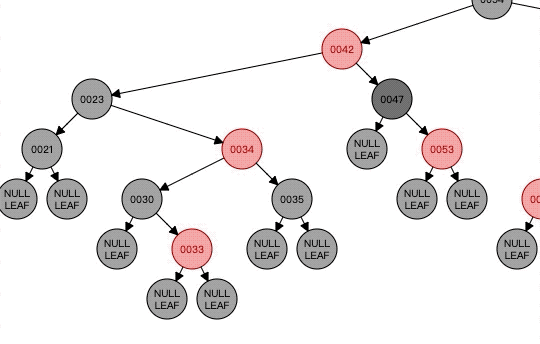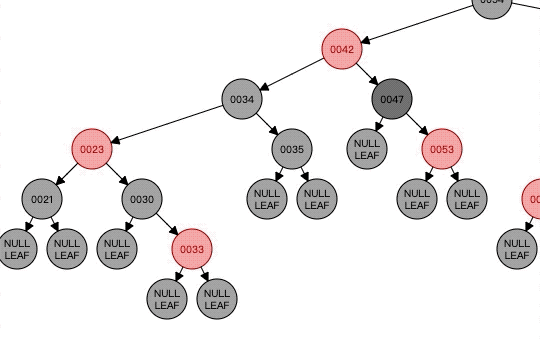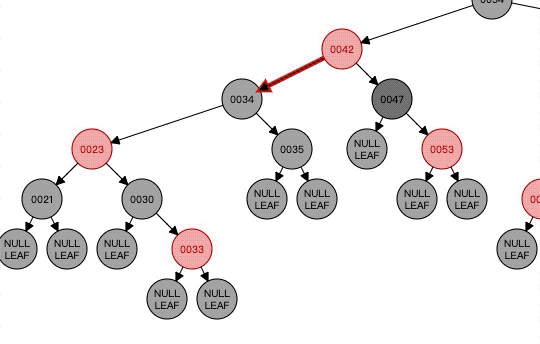
看看这个，接着上一个的，因为47那个点的黑色节点明显少了。所以以它为N，它作为父节点的右节点，然后它的兄弟节点是黑色，兄弟节点的右孩子是红色，左孩子是黑色，所以以23为中心进行左旋。至此Case6已经执行完毕。c x
这时候我们可以看到47这边还是少了，然后我们看看47的兄弟节点34是黑色的，34的左孩子是红色，不管34的右孩子啥颜色，也不管47的父节点什么颜色，现在满足的是Case4了，这时候应该以父节点42为轴进行右旋，并且将父节点颜色给兄弟节点34，然后父节点设置为黑色，将兄弟节点的左孩子变成黑色。结果如下

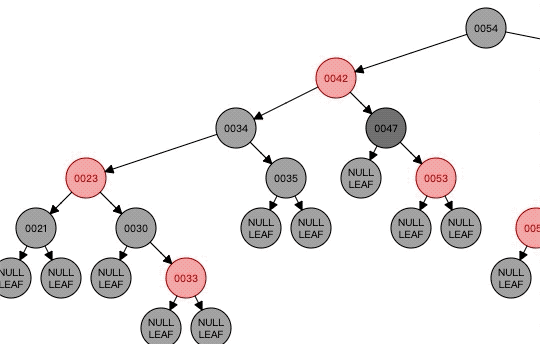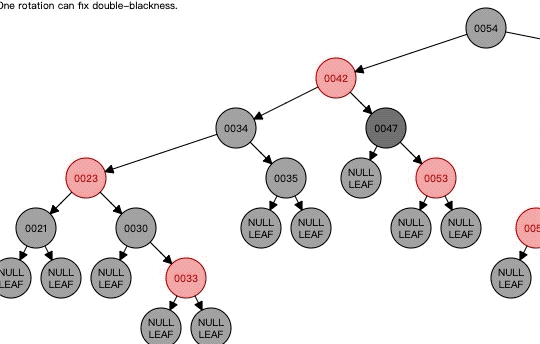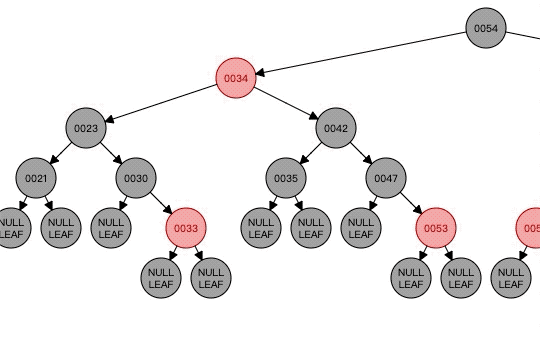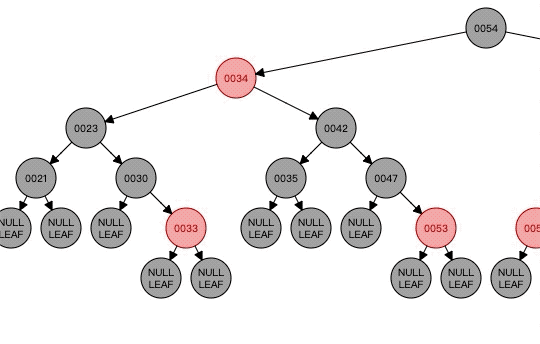
最终的树结构就是这样子了。

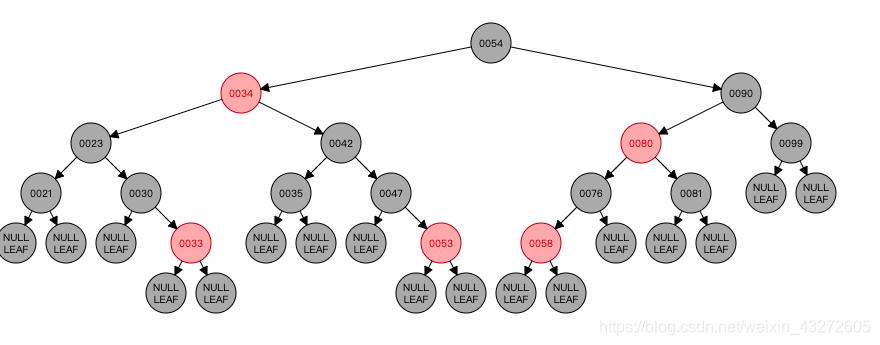
这样，所有的删除情况就列举出来了，当然，我列举的有一部分其实可以归于一类，但是我还是分成了几种，大家可以去看官方的操作。下面总结一下删除

代码实现红黑树