非极大值抑制（Non-Maximum Suppression，NMS）

概述

非极大值抑制（Non-Maximum Suppression，NMS），顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。这里不讨论通用的NMS算法(参考论文《Efficient Non-Maximum Suppression》对1维和2维数据的NMS实现)，而是用于目标检测中提取分数最高的窗口的。例如在行人检测中，滑动窗口经提取特征，经分类器分类识别后，每个窗口都会得到一个分数。但是滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域里分数最高（是行人的概率最大），并且抑制那些分数低的窗口。

NMS在计算机视觉领域有着非常重要的应用，如视频目标跟踪、数据挖掘、3D重建、目标识别、目标检测（DPM，YOLO，SSD，Faster R-CNN）以及纹理分析等。

为什么要用非极大值抑制

以目标检测为例：目标检测的过程中在同一目标的位置上会产生大量的候选框，这些候选框相互之间可能会有重叠，此时我们需要利用非极大值抑制找到最佳的目标边界框，消除冗余的边界框。Demo如下图：

 

Object Detection

左图是人脸检测的候选框结果，每个边界框有一个置信度得分(confidence score)，如果不使用非极大值抑制，就会有多个候选框出现。右图是使用非极大值抑制之后的结果，符合我们人脸检测的预期结果。

IOU（区域交并比）

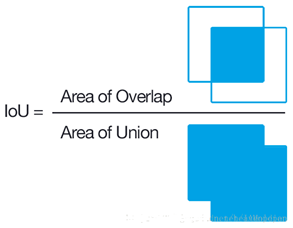
IOU的原称为Intersection over Union，也就是两个box区域的交集比上并集，下面的示意图就很好理解，用于确定两个框的位置像素距离~

思路：（注意维度一致）

• 首先计算两个box左上角点坐标的最大值和右下角坐标的最小值
• 然后计算交集面积
• 最后把交集面积除以对应的并集面积

其Pytorch源码为：（注意矩阵维度的变化）

# IOU计算
    # 假设box1维度为[N,4]   box2维度为[M,4]
    def iou(self, box1, box2):
        N = box1.size(0)
        M = box2.size(0)

        lt = torch.max(  # 左上角的点
            box1[:, :2].unsqueeze(1).expand(N, M, 2),   # [N,2]->[N,1,2]->[N,M,2]
            box2[:, :2].unsqueeze(0).expand(N, M, 2),   # [M,2]->[1,M,2]->[N,M,2]
        )

        rb = torch.min(
            box1[:, 2:].unsqueeze(1).expand(N, M, 2),
            box2[:, 2:].unsqueeze(0).expand(N, M, 2),
        )

        wh = rb - lt  # [N,M,2]
        wh[wh < 0] = 0   # 两个box没有重叠区域
        inter = wh[:,:,0] * wh[:,:,1]   # [N,M]

        area1 = (box1[:,2]-box1[:,0]) * (box1[:,3]-box1[:,1])  # (N,)
        area2 = (box2[:,2]-box2[:,0]) * (box2[:,3]-box2[:,1])  # (M,)
        area1 = area1.unsqueeze(1).expand(N,M)  # (N,M)
        area2 = area2.unsqueeze(0).expand(N,M)  # (N,M)

        iou = inter / (area1+area2-inter)
        return iou

其中：

• torch.unsqueeze(1) 表示增加一个维度，增加位置为维度1
• torch.squeeze(1) 表示减少一个维度

NMS（非极大抑制）

NMS算法一般是为了去掉模型预测后的多余框，其一般设有一个nms_threshold=0.5，具体的实现思路如下：

1. 选取这类box中scores最大的哪一个，记为box_best，并保留它
2. 计算box_best与其余的box的IOU
3. 如果其IOU>0.5了，那么就舍弃这个box（由于可能这两个box表示同一目标，所以保留分数高的哪一个）
4. 从最后剩余的boxes中，再找出最大scores的哪一个，如此循环往复

# NMS算法
    # bboxes维度为[N,4]，scores维度为[N,], 均为tensor
    def nms(self, bboxes, scores, threshold=0.5):
        x1 = bboxes[:,0]
        y1 = bboxes[:,1]
        x2 = bboxes[:,2]
        y2 = bboxes[:,3]
        areas = (x2-x1)*(y2-y1)   # [N,] 每个bbox的面积
        _, order = scores.sort(0, descending=True)    # 降序排列

        keep = []
        while order.numel() > 0:       # torch.numel()返回张量元素个数
            if order.numel() == 1:     # 保留框只剩一个
                i = order.item()
                keep.append(i)
                break
            else:
                i = order[0].item()    # 保留scores最大的那个框box[i]
                keep.append(i)

            # 计算box[i]与其余各框的IOU(思路很好)
            xx1 = x1[order[1:]].clamp(min=x1[i])   # [N-1,]
            yy1 = y1[order[1:]].clamp(min=y1[i])
            xx2 = x2[order[1:]].clamp(max=x2[i])
            yy2 = y2[order[1:]].clamp(max=y2[i])
            inter = (xx2-xx1).clamp(min=0) * (yy2-yy1).clamp(min=0)   # [N-1,]

            iou = inter / (areas[i]+areas[order[1:]]-inter)  # [N-1,]
            idx = (iou <= threshold).nonzero().squeeze() # 注意此时idx为[N-1,] 而order为[N,]
            if idx.numel() == 0:
                break
            order = order[idx+1]  # 修补索引之间的差值
        return torch.LongTensor(keep)   # Pytorch的索引值为LongTensor

其中：

• torch.numel() 表示一个张量总元素的个数
• torch.clamp(min, max) 设置上下限
• tensor.item() 把tensor元素取出作为numpy数字

下面为算法测试效果（人头检测）：

• 不使用NMS算法（产生了40个预测框，都重复在一起）

• 使用NMS算法之后（产生了5个预测框）