P4097 [HEOI2013]Segment 李超线段树

$ \color{#0066ff}{ 题目描述 }$

要求在平面直角坐标系下维护两个操作：

1. 在平面上加入一条线段。记第 i 条被插入的线段的标号为 i
2. 给定一个数 k,询问与直线 x = k 相交的线段中，交点最靠上的线段的编号。

有n家洗车店从左往右排成一排，每家店都有一个正整数价格p[i]。有m个人要来消费，第i个人会驶过第a[i]个开始一直到第b[i]个洗车店，且会选择这些店中最便宜的一个进行一次消费。但是如果这个最便宜的价格大于c[i]，那么这个人就不洗车了。请给每家店指定一个价格，使得所有人花的钱的总和最大。

\(\color{#0066ff}{输入格式}\)

第一行一个整数 n，表示共 n 个操作

接下来 n 行，每行第一个数为 0 或 1

若该数为 0，则后面跟着一个正整数 k，表示询问与直线 x = ((k + lastans – 1)%39989+1)相交的线段中交点（包括在端点相交的情形）最靠上的线段的编号，其中%表示取余。若某条线段为直线的一部分，则视作直线与线段交于该线段 y 坐标最大处。若有多条线段符合要求，输出编号最小的线段的编号

若该数为 1，则后面跟着四个正整数 x0, y0, x1, y1，表示插入一条两个端点为 ((x0+lastans-1)%39989+1,(y0+lastans-1)%\(10^9\)+1)和 ((x1+lastans-1)%39989+1,(y1+lastans-1)%\(10^9\)+1) 的线段

其中 lastans 为上一次询问的答案。初始时 lastans=0

\(\color{#0066ff}{输出格式}\)

对于每个 0 操作，输出一行，包含一个正整数，表示交点最靠上的线段的编 号。若不存在与直线相交的线段，答案为 0

\(\color{#0066ff}{输入样例}\)

6 
1 8 5 10 8 
1 6 7 2 6 
0 2 
0 9 
1 4 7 6 7 
0 5

\(\color{#0066ff}{输出样例}\)

2 
0 
3

\(\color{#0066ff}{数据范围与提示}\)

对于 30%的数据，n ≤ 1000
对于 100%的数据，1 ≤ n ≤ \(10^5\), 1 ≤ k, x0, x1 ≤ 39989, 1 ≤ y0 ≤ y1 ≤ \(10^9\)

\(\color{#0066ff}{题解}\)

考虑用线段树维护下标为x的最大的y

那么考虑两条直线

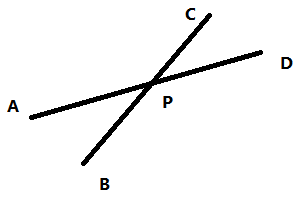
如果出现如图情况，显然BP和PD对答案其实就没有贡献了

线段树实际上维护的就是一个折线

但是对于一个区间，没办法记录一个直线，怎么办？

反正查询也是单点查询，我们可以考虑记录使得当前区间的mid位置的值最优的直线

然后看交点的位置，判断往哪个方向递归

实际上并不用求交点，更新当前区间的时候，如果现在的比当前区间的线段更优，就交换一下，用它去更新子树

这时候只要判断斜率就知道改往哪个方向递归了

这样操作其实是一种类似于标记永久化的东东，于是单点查询的时候要沿途取最优！

#include <bits/stdc++.h>
#define LL long long
#define mid ((l + r) >> 1)
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 1e5 + 10;
const int mod1 = 39989;
const int mod2 = 1e9;
const double eps = 1e-6;
struct St {
protected:
    struct node {
        int s1, s2, id; double t1, t2;  //线段两个端点，对应的y
        node *ch[2];    
        node(int s1 = 0, int s2 = 0, int id = 0, double t1 = 0, double t2 = 0): s1(s1), s2(s2), id(id), t1(t1), t2(t2) {
            ch[0] = ch[1] = NULL;
        } 
        double gety(int x) { return s1 == s2? t1 : t1 + (getk() * (x - s1)); } //把x带入获得y
        double getk() { return (double)(t2 - t1) / (double)(s2 - s1); }   //斜率
        double getmin() { return std::min(t1, t2); }   //区间最小y
        double getmax() { return std::max(t1, t2); }   //区间最大y
        void ltrn(int x) { t1 = gety(x); s1 = x; }     //有一个x = (this)x的直线截取当前线段，取右边
        void rtrn(int x) { t2 = gety(x); s2 = x; }     //同上，取左边，就是缩小线段到当前区间范围内
    }*root, pool[maxn], *tail;
    int n;
    bool check(node *a, node *b, int x) {  //看看把x带入a是否比b优
        double vala = a->gety(x), valb = b->gety(x);
        return fabs(vala - valb) <= eps? a->id < b->id : vala > valb;
    }
    void build(node *&o, int l, int r) {
    	o = new node(l, r);
        if(l == r) return;
        build(o->ch[0], l, mid);
        build(o->ch[1], mid + 1, r); 
    }
    node *query(node *o, int l, int r, int pos) {
        if(l == r) return o;
        node *ans;
        if(pos <= mid) ans = query(o->ch[0], l, mid, pos);
        else ans = query(o->ch[1], mid + 1, r, pos);
        return check(ans, o, pos)? ans : o;   //每次取最优
    }
    void lazy(node *o, int l, int r, node *k) {
        if(o->s1 > k->s1) k->ltrn(o->s1);   //缩小线段的x范围到当前区间
        if(o->s2 < k->s2) k->rtrn(o->s2);
        if(check(k, o, mid)) {
        	std::swap(o->s1, k->s1);  //更优则交换
        	std::swap(o->s2, k->s2);
        	std::swap(o->t1, k->t1);
        	std::swap(o->t2, k->t2);
        	std::swap(o->id, k->id);
        }
        if(o->getmin() >= k->getmax()) return;  //没有贡献
        if(o->getk() <= k->getk()) lazy(o->ch[1], mid + 1, r, k);
        else lazy(o->ch[0], l, mid, k);
    }
    void ins(node *o, int l, int r, node *k) {  
        if(k->s1 > r || k->s2 < l) return;
    	node *newk = new(tail++) node(); *newk = *k; //这里必须开一个新的点，要保证递归完k并没有改变
        if(o->s1 > newk->s1) newk->ltrn(o->s1);
        if(o->s2 < newk->s2) newk->rtrn(o->s2);
        if(l == newk->s1 && r == newk->s2) return lazy(o, l, r, newk);
        ins(o->ch[0], l, mid, newk);
        ins(o->ch[1], mid + 1, r, newk);
    }
public:
    void init(int n) { this->n = n; root = NULL; build(root, 1, n); }
    void ins(int s1, int s2, int id, int t1, int t2) {
        tail = pool;
        node *o = new node(s1, s2, id, t1, t2);
        if(s1 == s2) o->t1 = o->t2 = o->getmax();
        ins(root, 1, n, o);
    }
    int query(int pos) { return query(root, 1, n, pos)->id; }
}T;
int main(){
    T.init(mod1);
    int ans = 0, cnt = 0, s1, s2, t1, t2;
    for(int Q = in(); Q --> 0;) {
        if (!in()) printf("%d\n", ans = T.query((in() + ans - 1) % mod1 + 1));
        else{
            s1 = (in() + ans - 1) % mod1 + 1;
            t1 = (in() + ans - 1) % mod2 + 1;
            s2 = (in() + ans - 1) % mod1 + 1;
            t2 = (in() + ans - 1) % mod2 + 1;
            if(s1 > s2) std::swap(s1, s2), std::swap(t1, t2);
            T.ins(s1, s2, ++cnt, t1, t2);
        }
    }
}