PTA-oop第二次博客2022.10.25

一.前言

题目集四:

　　刚刚经历完第三次作业洗礼,紧接着又遇到了如此重量级的凸四边形的计算,一开始是非常痛苦的,由于一开始动手写四边形的计算时还没有学习继承导致四边形的代码和三角形代码高度相似,虽然在之后学习了继承,老师又让我们重构四边形的代码当时我还以为自己写的挺好,回过头来看,其实完全没有体现的继承,可能是在刚学习玩继承之后没有完全理解,导致代码写的及其混乱,又加上题目难度较高,总结下来,虽然是通过了所有测试点,我不认为这是一次很成功的作业.

题目集五:

　　五边形以及多边形应该是这几次作业最难的一次了,一道题目甚至分成了两次,同样在写第一题时没有学到继承,代码过于冗余,以至于写第二道题目时根本无从下手,在学完继承过后,新建一个多边形父类,再加上自己的思考,成功的缩短了代码的总长度,在全部写完题目之后再看这几道题,其实没什么难的

期中考试:

　　考试的目的就是检验我们这半个学期以来我们学到的东西,考察内容包括了封装,继承以及多态,难度一般.

二.设计与分析

题目一:

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

选项1、2、3中，若四边形四个点中有重合点，输出"points coincide"。
选项4中，若前两个输入线的点重合，输出"points coincide"。

public class Main {

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        Format P = new Format();
        P.s = input.nextLine();
        if (!P.matche()) {
            System.out.println("Wrong Format");
            return;
        }
        if (P.numberNo() == 1) {
            if (P.numberPoints() == 4) {
                Quadrilateral a = new Quadrilateral(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4));
                if (a.isCoincide())
                    System.out.print("points coincide");
                else
                    System.out.print(a.isQuadrilateral() + " " + a.isParallelogram());
            } else
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 2) {
            if (P.numberPoints() == 4) {
                Quadrilateral a = new Quadrilateral(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4));
                if (a.isCoincide())
                    System.out.print("points coincide");
                else if (!a.isQuadrilateral())
                    System.out.print("not a quadrilateral");
                else
                    System.out.print(a.isDiamond() + " " + a.isRectangle() + " " + a.isSquare());
            } else
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 3) {
            if (P.numberPoints() == 4) {
                Quadrilateral a = new Quadrilateral(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4));
                if (a.isCoincide())
                    System.out.print("points coincide");
                else if (!a.isQuadrilateral())
                    System.out.print("not a quadrilateral");
                else {
                    System.out.print(!a.isConcave() + " ");
                    P.FormatOut(a.GetCircle());
                    System.out.print(" ");
                    P.FormatOut(a.GetArea());
                }
            } else
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 4) {
            if (P.numberPoints() == 6) {
                line l = new line(P.getPoints(1), P.getPoints(2));
                if (P.getPoints(1).coincide(P.getPoints(2))) {
                    System.out.print("points coincide");
                    return;
                }
                Quadrilateral a = new Quadrilateral(P.getPoints(3), P.getPoints(4), P.getPoints(5), P.getPoints(6));
                if (!a.isQuadrilateral()) {
                    ArrayList<points> pList = a.GetPoint(a.P);
                    if (pList.size() == 3) {
                        triangle t = new triangle(pList.get(0),pList.get(1),pList.get(2));
                        if (t.isTriangle()) {
                            if (t.triangleCoincideline(l)) {
                                System.out.print("The line is coincide with one of the lines");
                                return;
                            }
                            t.LineCutPoly(l);
                        }
                    } else
                        System.out.print("not a quadrilateral or triangle");
                } else {
                    if (a.lineCoincide(l)) {
                        System.out.print("The line is coincide with one of the lines");
                        return;
                    }
                    a.lineCoincide(l);
                }
            } else
                System.out.println("wrong number of points");
        } else {
            if (P.numberPoints() == 5) {
                points p = new points(P.getPoints(1));
                Quadrilateral a = new Quadrilateral(P.getPoints(2), P.getPoints(3), P.getPoints(4), P.getPoints(5));
                if (!a.isQuadrilateral()) {
                    ArrayList<points> pList = a.GetPoint(a.P);
                    if (pList.size() == 3) {
                        triangle t = new triangle(pList.get(0),pList.get(1),pList.get(2));
                        if (t.isTriangle()) {
                            if (!t.judgeOnTriangle(p)) {
                                if (t.IsPointInPoly(p))
                                    System.out.print("in the triangle");
                                else
                                    System.out.print("outof the triangle");
                            } else
                                System.out.print("on the triangle");
                        }else
                            System.out.print("not a quadrilateral or triangle");
                    } else
                        System.out.print("not a quadrilateral or triangle");
                } else {
                    if (!a.onQuadrilateral(p)) {
                        if (a.IsPointInPoly(p))
                            System.out.print("in the quadrilateral");
                        else
                            System.out.print("outof the quadrilateral");
                    } else
                        System.out.print("on the quadrilateral");
                }
            } else
                System.out.println("wrong number of points");
        }
    }

}
class Format {
    String s;
    public boolean matche() {
        String regx = "([+-]?[0-9]+)(.[0-9]+)?";
        if (this.s.charAt(0) > '5' || this.s.charAt(0) < '1')
            return false;
        if (this.s.charAt(1) != ':')
            return false;
        String arr = this.s.substring(2);
        String arr1[] = arr.split(" ");
        for (int i = 0; i < arr1.length; i++) {
            String arr2[] = arr1[i].split(",");
            if (arr2.length != 2)
                return false;
            if (!arr2[0].matches(regx))
                return false;
            if (!arr2[1].matches(regx))
                return false;
        }
        return true;
    }
    public int numberNo() {
        return Integer.parseInt(this.s.split(":")[0]);
    }

    public int numberPoints() {
        String arr[] = this.s.split(" |:");
        return arr.length - 1;
    }

    public points getPoints(int index) {
        points a = new points();
        String arr[] = this.s.split(":")[1].split(" ");
        a.x = Double.parseDouble(arr[index - 1].split(",")[0]);
        a.y = Double.parseDouble(arr[index - 1].split(",")[1]);
        return a;
    }

    public void FormatOut(double x) {
        if ((x * 1e3) % 10 != 0)
            System.out.printf("%.3f", x);
        else
            System.out.print(x);
    }
}
class line {
    points a, b;
    line (){
        
    }
    line (points a,points b){
        this.a=a;
        this.b=b;
    }
    public boolean isK() {
        if (this.a.x == this.b.x)
            return false;
        else
            return true;
    }

    public double getK() {
        return (this.a.y - this.b.y) / (this.a.x - this.b.x);
    }

    public double getB() {
        return this.a.y - this.a.x * this.getK();
    }

    public double getDistance(points a) {
        if (this.isK()) {
            double numerator = Math.abs(getK() * a.x - a.y + this.getB());
            double denominator = Math.sqrt(1 + Math.pow(this.getK(), 2));
            return numerator / denominator;
        } else
            return Math.abs(this.a.x - a.x);
    }

    public boolean isOnline(points a) {
        if (this.getA1() * a.x + this.getB1() * a.y == this.getC1())
            return true;
        else
            return false;
    }

    public double getA1() {
        return this.b.y - this.a.y;
    }

    public double getB1() {
        return this.a.x - this.b.x;
    }

    public double getC1() {
        return this.a.x * this.getA1() + this.a.y * this.getB1();
    }

    public points getIntersection(line a) {
        double A, B;
        double A1, B1, C1;
        double A2, B2, C2;
        A1 = a.getA1();
        B1 = a.getB1();
        C1 = a.getC1();
        A2 = this.getA1();
        B2 = this.getB1();
        C2 = this.getC1();
        double X, Y;
        A = (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1);
        B = (A1 * C2 - A2 * C1) / (A1 * B2 - A2 * B1);
        points d = new points();
        d.x = A;
        d.y = B;
        return d;
    }

    public boolean isParallel(line a) {
        if (this.isK() && a.isK()) {
            if (this.getK() == a.getK())
                return true;
            else
                return false;
        } else if (!this.isK() && !a.isK())
            return true;
        else
            return false;
    }
    public boolean isVertical(line a) {
        if(this.isK()&&a.isK())
        {
            if(this.getK()*a.getK()==-1)
                return true;
            else
                return false;
        }
        else if(!this.isK()&&a.getK()==0)
            return true;
        else if(this.getK()==0&&!a.isK())
            return true;
        else
            return false;
    }
    public boolean isBetween(points a) {
        if (a.x >= Math.min(this.a.x, this.b.x) && a.x <= Math.max(this.a.x, this.b.x)
                && a.y >= Math.min(this.a.y, this.b.y) && a.y <= Math.max(this.a.y, this.b.y))
            return true;
        else
            return false;
    }

    public double lineLength() {
        return this.a.getDistance(this.b);
    }

    public boolean lineCoincide(line a) {
        if (this.isK() && a.isK()) {
            if (this.isParallel(a) && this.getB() == a.getB())
                return true;
            else
                return false;
        } else if (!this.isK() && !a.isK()) {
            if (this.a.x == a.a.x)
                return true;
            else
                return false;
        } else
            return false;
    }
    boolean PointOnOneSide(points a) {
        if(a.x*this.getA1()+a.y*this.getB1()-this.getC1()>0)
            return true;
        else
            return false;
    }
    boolean PointOnOneSide1(points a) {
        if(a.x*this.getA1()+a.y*this.getB1()-this.getC1()<0)
            return true;
        else
            return false;
    }
}
class points {
    double x,y;
    points(){
        
    }
    points(points a){
        this.x=a.x;
        this.y=a.y;
    }
    points(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double getDistance(points a) {
        return Math.sqrt(Math.pow(this.x-a.x,2)+Math.pow(this.y-a.y,2));
    }
    public double getSquare(points a) {
        return Math.pow(this.x-a.x,2)+Math.pow(this.y-a.y,2);
    }
    public boolean coincide(points a) {
        if(this.x==a.x&&this.y==a.y)
            return true;
        else
            return false;
    }
    public boolean onSameLine(points a,points b) {
        line l=new line(a,b);
        return l.isOnline(this)&&l.isBetween(this);
    }
    public boolean isSameElemts(points p[],int length) {
        for(int i=0;i<length;i++)
        {
            if(this.coincide(p[i]))
                return true;
        }
        return false;
    }
    public boolean isSameElemts(ArrayList<points> P) {
        if(P.size()==0)
            return false;
        for(int i=0;i<P.size();i++)
        {
            if(this.coincide(P.get(i)))
                return true;
        }
        return false;
    }
}
class Poly {
    ArrayList<points> P = new ArrayList<points>();
    ArrayList<line> L = new ArrayList<line>();

    Poly() {

    }

    Poly(ArrayList<points> p) {
        this.P = this.GetPoint(p);
        for (int i = 0; i < P.size(); i++) {
            line l = new line(P.get(i), P.get((i + 1) % P.size()));
            L.add(l);
        }
    }
    ArrayList<points> GetPoint(ArrayList<points> p2) {
        ArrayList<points> P = new ArrayList<points>();
        for (int i = 0; i < p2.size(); i++)
            for (int j = i + 1; j < p2.size();) {
                if (p2.get(i).coincide(p2.get(j)))
                    p2.remove(j);
                else
                    j++;
            }
        for (int i = 0; i < p2.size(); i++) {
            if (!p2.get(i).onSameLine(p2.get((i + p2.size() - 1) % p2.size()), p2.get((i + p2.size() + 1) % p2.size())))
                P.add(p2.get(i));
        }
        return P;
    }
    ArrayList<points> GetIntersection(line l) {
        ArrayList<points> inter = new ArrayList<points>();
        for (int i = this.P.size() - 1; i >= 0; i--) {
            if (!L.get(i).isParallel(l)) {
                points a = new points();
                a = L.get(i).getIntersection(l);
                if (!a.isSameElemts(inter) && L.get(i).isBetween(a)) {
                    if (!(i == this.P.size() - 1 && a.coincide(P.get(0))))
                        inter.add(a);
                }
            }
        }
        return inter;
    }
    double GetArea() {
        double area = 0;
        for (int i = 0; i < this.P.size(); i++)
            area = 0.5 * (P.get(i).x * P.get((i + 1) % this.P.size()).y - P.get(i).y * P.get((i + 1) % this.P.size()).x)
                    + area;
        return Math.abs(area);
    }

    double GetCircle() {
        double circle = 0;
        for (int i = 0; i < this.P.size(); i++)
            circle = P.get(i).getDistance(P.get((i + 1) % this.P.size())) + circle;
        return circle;
    }

    double GetLineLength(int i) {
        return P.get(i).getDistance(P.get((i + 1) % this.P.size()));
    }
    void LineCutPoly(line l) {
        Format f = new Format();
        ArrayList<points> inter = new ArrayList<points>();
        inter = this.GetIntersection(l);
        System.out.print(inter.size() + " ");
        if (inter.size() == 2) {
            for (int i = 0; i < this.P.size(); i++) {
                if(l.getK()>0) {
                    if (l.PointOnOneSide(this.P.get(i)))
                        inter.add(this.P.get(i));
                }
                else
                {
                    if (l.PointOnOneSide1(this.P.get(i)))
                        inter.add(this.P.get(i));
                }
            }
            Poly cutpoly = new Poly(inter);
            f.FormatOut(Math.min(this.GetArea() - cutpoly.GetArea(), cutpoly.GetArea()));
            System.out.print(" ");
            f.FormatOut(Math.max(this.GetArea() - cutpoly.GetArea(), cutpoly.GetArea()));
        }
    }
    boolean IsPointInPoly(points p) {
        double sumarea = 0;
        for (int i = 0; i < this.P.size(); i++) {
            triangle t = new triangle(p, this.P.get(i), this.P.get((i + 1) % this.P.size()));
            sumarea = t.GetArea() + sumarea;
        }
        return sumarea == this.GetArea();
    }
}
Quadrilateral extends Poly{

    points a, b, c, d;
    line A = new line();
    line B = new line();
    line C = new line();
    line D = new line();
    

    Quadrilateral(points a, points b, points c, points d) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        P.add(d);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }

    Quadrilateral() {
    }
    boolean isQuadrilateral() {
        triangle a = new triangle(this.a, this.b, this.c);
        triangle b = new triangle(this.b, this.c, this.d);
        triangle c = new triangle(this.c, this.d, this.a);
        triangle d = new triangle(this.d, this.a, this.b);
        if (a.isTriangle() && b.isTriangle() && c.isTriangle() && d.isTriangle()) {
            points p = new points();
            if (!this.A.isParallel(this.C)) {
                p = this.A.getIntersection(this.C);
                if (this.A.isBetween(p) && this.C.isBetween(p))
                    return false;
            }
            if (!this.B.isParallel(this.D)) {
                p = this.B.getIntersection(this.D);
                if (this.B.isBetween(p) && this.D.isBetween(p))
                    return false;
            }
            return true;
        } else
            return false;
    }

    boolean isDiamond() {
        if (this.isParallelogram()) {
            if (this.A.lineLength() == this.B.lineLength())
                return true;
            else
                return false;
        } else
            return false;
    }

    boolean isRectangle() {
        if (this.isParallelogram()) {
            if (this.A.isVertical(this.B))
                return true;
            else
                return false;
        } else
            return false;
    }

    boolean isSquare() {
        if (this.isRectangle()) {
            if (this.A.lineLength() == this.B.lineLength())
                return true;
            else
                return false;
        } else
            return false;
    }

    boolean isParallelogram() {
        if (this.isQuadrilateral()) {
            if (this.A.isParallel(this.C) && this.B.isParallel(this.D))
                return true;
            else
                return false;
        } else
            return false;
    }

    boolean isCoincide() {
        if (this.a.coincide(this.b) || this.b.coincide(this.c) || this.c.coincide(this.d) || this.d.coincide(this.a))
            return true;
        else
            return false;
    }

    boolean isConcave() {// 凹
        triangle a = new triangle(this.a, this.b, this.c);
        triangle b = new triangle(this.b, this.c, this.d);
        triangle c = new triangle(this.c, this.d, this.a);
        triangle d = new triangle(this.d, this.a, this.b);
        if (a.GetArea() + c.GetArea() == b.GetArea() + d.GetArea())
            return false;
        else
            return true;
    }

    boolean lineCoincide(line l) {
        if (A.lineCoincide(l) || B.lineCoincide(l) || C.lineCoincide(l)||D.lineCoincide(l))
            return true;
        else
            return false;
    }

    boolean onQuadrilateral(points a) {
        if(this.A.isBetween(a)&&this.A.isOnline(a)||this.B.isBetween(a)&&this.B.isOnline(a)||this.C.isBetween(a)&&this.C.isOnline(a)||this.D.isBetween(a)&&this.D.isOnline(a))
            return true;
        else
            return false;
    }
}
class triangle extends Poly{// 点小写,边大写
    points a, b, c;
    line A = new line();
    line B = new line();
    line C = new line();

    public triangle(points a, points b, points c) {
        this.a = a;
        this.b = b;
        this.c = c;
        A.a = this.b;
        A.b = this.c;
        B.a = this.c;
        B.b = this.a;
        C.a = this.b;
        C.b = this.a;
        P.add(a);
        P.add(b);
        P.add(c);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    public triangle(){
        
    }
    public double getA() {
        return this.b.getDistance(c);
    }

    public double getB() {
        return this.a.getDistance(c);
    }

    public double getC() {
        return this.b.getDistance(a);
    }

    public boolean isTriangle() {
        if (this.GetArea() != 0)
            return true;
        else
            return false;
    }

    public boolean judgeOnTriangle(points a) {
        // TODO 自动生成的方法存根
        line A = new line();
        line B = new line();
        line C = new line();
        A.a = this.b;
        A.b = this.c;
        B.a = this.c;
        B.b = this.a;
        C.a = this.b;
        C.b = this.a;
        if (A.getDistance(a) == 0 || B.getDistance(a) == 0 || C.getDistance(a) == 0)
            return true;
        else
            return false;
    }

    public boolean triangleCoincideline(line a) {
        line A = new line();
        line B = new line();
        line C = new line();
        A.a = this.b;
        A.b = this.c;
        B.a = this.c;
        B.b = this.a;
        C.a = this.b;
        C.b = this.a;
        if (A.lineCoincide(a) || B.lineCoincide(a) || C.lineCoincide(a))
            return true;
        else
            return false;
    }
}

 

 

 

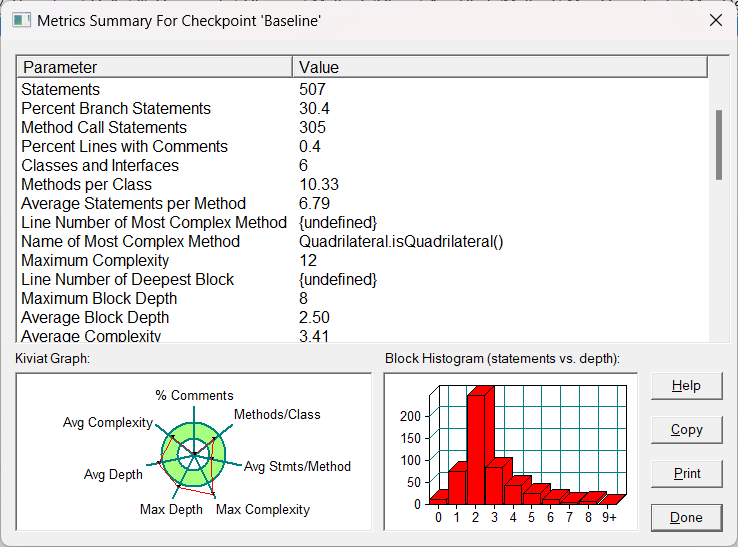
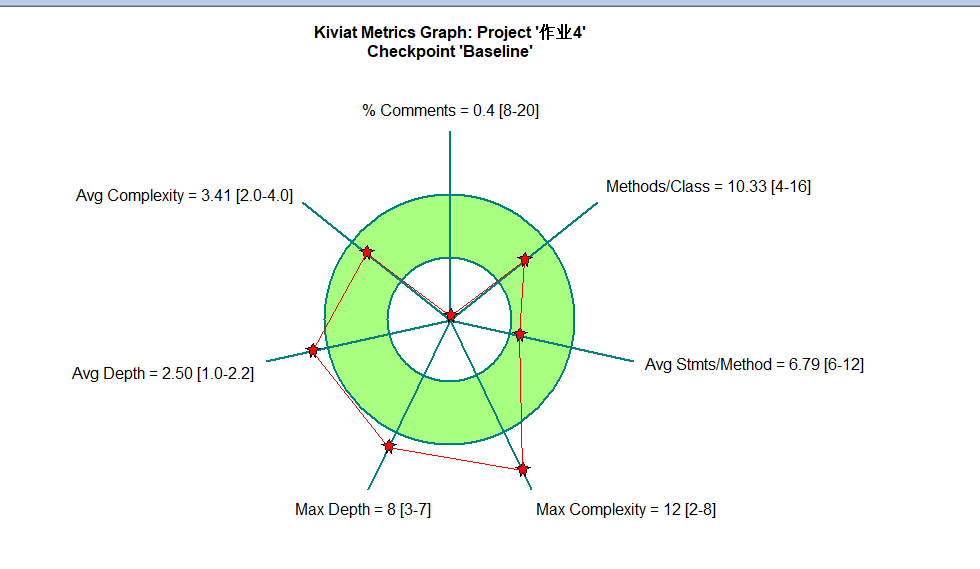
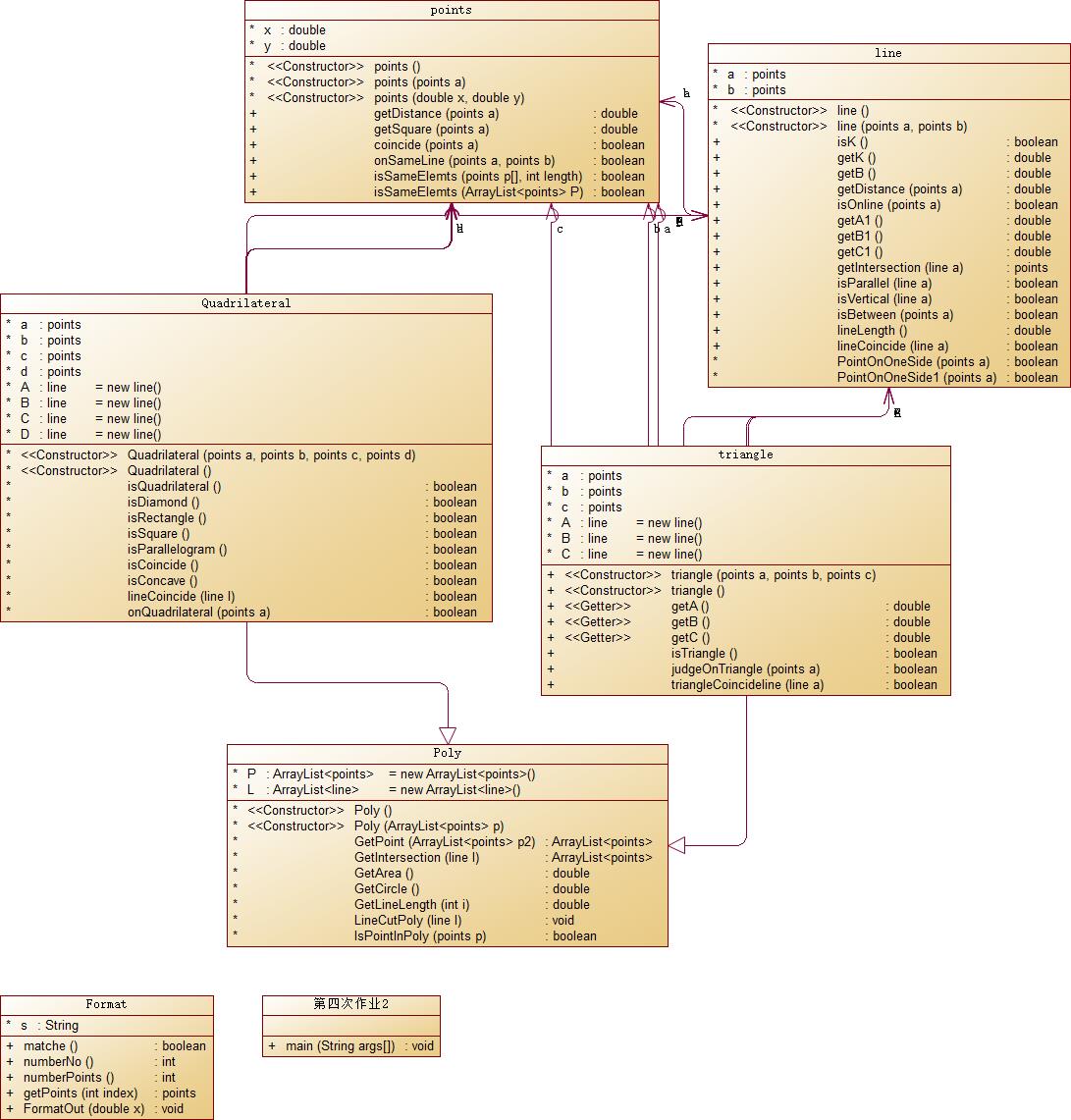
代码在全部写完之后又重构过一次,也是因为当时自己对继承的理解并不够深刻,导致最后改出来的代码很烂,圈复杂度达到了31,有许多的四边形和三角形共同的操作没有能够放进父类里,在写博客之前只好花一点时间重新写了多边形类,虽然代码有所改善,但是最大复杂度依旧没有在合理区间,还有很大改进空间

题目二:

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon

5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

 

第一题

import java.util.Scanner;
import java.util.ArrayList;

public class Main {

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        Format P = new Format();
        P.s = input.nextLine();
        if (!P.matche()) {
            System.out.println("Wrong Format");
            return;
        }
        if (P.numberNo() == 1) {
            if (P.numberPoints() == 5) {
                Pentagon a = new Pentagon(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4),
                        P.getPoints(5));
                System.out.print(a.isPentagon());
            } elsemvn m 
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 2) {
            if (P.numberPoints() == 5) {
                Pentagon a = new Pentagon(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4),
                        P.getPoints(5));
                if (a.isPentagon()) {
                    System.out.print(!a.isConcave());
                    if (!a.isConcave()) {
                        System.out.print(" ");
                        P.FormatOut(a.GetCircle());
                        System.out.print(" ");
                        P.FormatOut(a.GetArea());
                    }
                } else
                    System.out.print("not a pentagon");
            } else
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 3) {
            if (P.numberPoints() == 7) {
                line l = new line(P.getPoints(1), P.getPoints(2));
                Pentagon a = new Pentagon(P.getPoints(3), P.getPoints(4), P.getPoints(5), P.getPoints(6),
                        P.getPoints(7));
                if (a.isPentagon()) {
                    a.LineCutPoly(l);
                } else if (a.P.size() == 4) {
                    Quadrilateral Q = new Quadrilateral(a.P);
                    if (Q.isQuadrilateral()) {
                        if (Q.isCoincideLine(l)) {
                            System.out.print("The line is coincide with one of the lines");
                            return;
                        }
                        a.LineCutPoly(l);
                    }
                } else if (a.P.size() == 3) {
                    triangle t = new triangle(a.P);
                    if (t.isTriangle()) {
                        a.LineCutPoly(l);
                    }
                } else
                    System.out.print("not a polygon");
            } else
                System.out.println("wrong number of points");
        }
    }
}
class Format {
    String s;
    public boolean matche() {
        String regx = "[+-]?([1-9]\\d*|0)(\\.\\d+)?";
        if (this.s.charAt(1) != ':')
            return false;
        String arr = this.s.substring(2);
        String arr1[] = arr.split(" ");
        for (int i = 0; i < arr1.length; i++) {
            String arr2[] = arr1[i].split(",");
            if (arr2.length != 2)
                return false;
            if (!arr2[0].matches(regx))
                return false;
            if (!arr2[1].matches(regx))
                return false;
        }
        return true;
    }
    public int numberNo() {
        return Integer.parseInt(this.s.split(":")[0]);
    }

    public int numberPoints() {
        String arr[] = this.s.split(" |:");
        return arr.length - 1;
    }

    public points getPoints(int index) {
        points a = new points();
        String arr[] = this.s.split(":")[1].split(" ");
        a.x = Double.parseDouble(arr[index - 1].split(",")[0]);
        a.y = Double.parseDouble(arr[index - 1].split(",")[1]);
        return a;
    }

    public void FormatOut(double x) {
        if ((x * 1e3) % 10 != 0)
            System.out.printf("%.3f", x);
        else
            System.out.print(x);
    }
}
class line {
    points a, b;

    line() {
    }

    line(points a, points b) {
        this.a = a;
        this.b = b;
    }

    public boolean isK() {
        if (this.a.x == this.b.x)
            return false;
        else
            return true;
    }

    public double getK() {
        return (this.a.y - this.b.y) / (this.a.x - this.b.x);
    }

    public double getB() {
        return this.a.y - this.a.x * this.getK();
    }

    public double getDistance(points a) {
        if (this.isK()) {
            double numerator = Math.abs(getK() * a.x - a.y + this.getB());
            double denominator = Math.sqrt(1 + Math.pow(this.getK(), 2));
            return numerator / denominator;
        } else
            return Math.abs(this.a.x - a.x);
    }

    public boolean isOnline(points a) {
        if (this.getDistance(a) == 0)
            return true;
        else
            return false;
    }

    public double getA1() {
        return this.b.y - this.a.y;
    }

    public double getB1() {
        return this.a.x - this.b.x;
    }

    public double getC1() {
        return this.a.x * this.getA1()+ this.a.y * this.getB1();
    }

    public points getIntersection(line a) {
        double A, B;
        double A1, B1, C1;
        double A2, B2, C2;
        A1 = a.getA1();
        B1 = a.getB1();
        C1 = a.getC1();
        A2 = this.getA1();
        B2 = this.getB1();
        C2 = this.getC1();
        double X, Y;
        A = (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1);
        B = (A1 * C2 - A2 * C1) / (A1 * B2 - A2 * B1);
        points d = new points();
        d.x = A;
        d.y = B;
        return d;
    }

    public boolean isParallel(line a) {
        if (this.isK() && a.isK()) {
            if (this.getK() == a.getK())
                return true;
            else
                return false;
        } else if (!this.isK() && !a.isK())
            return true;
        else
            return false;
    }

    public boolean isVertical(line a) {
        if (this.isK() && a.isK()) {
            if (this.getK() * a.getK() == -1)
                return true;
            else
                return false;
        } else if (!this.isK() && a.getK() == 0)
            return true;
        else if (this.getK() == 0 && !a.isK())
            return true;
        else
            return false;
    }

    public boolean isBetween(points a) {
        if (a.x >= Math.min(this.a.x, this.b.x) && a.x <= Math.max(this.a.x, this.b.x)
                && a.y >= Math.min(this.a.y, this.b.y) && a.y <= Math.max(this.a.y, this.b.y))
            return true;
        else
            return false;
    }

    public double lineLength() {
        return this.a.getDistance(this.b);
    }

    public boolean lineCoincide(line a) {
        if (this.isK() && a.isK()) {
            if (this.isParallel(a) && this.getB() == a.getB())
                return true;
            else
                return false;
        } else if (!this.isK() && !a.isK()) {
            if (this.a.x == a.a.x)
                return true;
            else
                return false;
        } else
            return false;
    }

    public boolean SegmentCoincide(line a) {
        boolean onLineA, onLineB, onLineC, onLineD;
        onLineA = this.a.onSameLine(a.a, a.b);//a在cd
        onLineB = this.b.onSameLine(a.a, a.b);//b在cd
        onLineC = a.a.onSameLine(this.a, this.b);//c在ab
        onLineD = a.b.onSameLine(this.a, this.b);//d在ab
        boolean coincide01 = (onLineA && onLineB) || (onLineC && onLineD);
        boolean coincide02 = (onLineB && onLineC) || (onLineA && onLineD );
        return (coincide01 || coincide02);
    }

    public boolean lineIntersection(line a) {
        if (Math.max(this.a.x, this.b.x) < Math.min(a.a.x, a.b.x)
                || Math.min(this.a.x, this.b.x) > Math.max(a.a.x, a.b.x)
                || Math.max(this.a.y, this.b.y) < Math.min(a.a.y, a.b.y)
                || Math.min(this.a.y, this.b.y) > Math.max(a.a.y, a.b.y)) {
            return false;
        }
        if (crossProduct(this.a.x - a.a.x, this.a.y - a.a.y, a.a.x - a.b.x, a.a.y - a.b.y)
                * crossProduct(this.b.x - a.a.x, this.b.y - a.a.y, a.a.x - a.b.x, a.a.y - a.b.y) > 0) {
            return false;
        }
        if (crossProduct(a.a.x - this.a.x, a.a.y - this.a.y, this.a.x - this.b.x, this.a.y - this.b.y)
                * crossProduct(a.b.x - this.a.x, a.b.y - this.a.y, this.a.x - this.b.x, this.a.y - this.b.y) > 0) {
            return false;
        }
        return true;
    }

    double crossProduct(double a1, double b1, double a2, double b2) {
        return a1 * b2 - b1 * a2;
    }
    boolean PointOnOneSide(points a) {
        if(a.x*this.getA1()+a.y*this.getB1()-this.getC1()>0)
            return true;
        else
            return false;
    }
    boolean PointOnOneSide1(points a) {
        if(a.x*this.getA1()+a.y*this.getB1()-this.getC1()<0)
            return true;
        else
            return false;
    }
}
class points {
    double x,y;
    points(){
        
    }
    points(points a){
        this.x=a.x;
        this.y=a.y;
    }
    public points(double x, double y) {
        this.x=x;
        this.y=y;
    }
    public double getDistance(points a) {
        return Math.sqrt(Math.pow(this.x-a.x,2)+Math.pow(this.y-a.y,2));
    }
    public double getSquare(points a) {
        return Math.pow(this.x-a.x,2)+Math.pow(this.y-a.y,2);
    }
    public boolean coincide(points a) {
        if(this.x==a.x&&this.y==a.y)
            return true;
        else
            return false;
    }
    public boolean onSameLine(points a,points b) {
        line l=new line(a,b);
        return l.isOnline(this)&&l.isBetween(this);
    }
    public boolean isSameElemts(ArrayList<points> P) {
        if(P.size()==0)
            return false;
        for(int i=0;i<P.size();i++)
        {
            if(this.coincide(P.get(i)))
                return true;
        }
        return false;
    }
}
class Poly {
    ArrayList<points> P = new ArrayList<points>();
    ArrayList<line> L = new ArrayList<line>();
    Poly(){
        
    }
    Poly(ArrayList<points> p) {        
        this.P=this.GetPoint(p);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    ArrayList<points> GetPoint(ArrayList<points> p2) {
        ArrayList<points> P=new ArrayList<points>();
        for(int i=0;i<p2.size();i++) 
            for(int j=i+1;j<p2.size();) {
                if(p2.get(i).coincide(p2.get(j)))
                        p2.remove(j);
                else
                        j++;
            }
        for(int i=0;i<p2.size();i++) {
            if(!p2.get(i).onSameLine(p2.get((i+p2.size()-1)%p2.size()), p2.get((i+p2.size()+1)%p2.size())))
                    P.add(p2.get(i));
        }
        return P;
    }
    double GetArea() {
        double area = 0;
        for (int i = 0; i < this.P.size(); i++)
            area = 0.5 * (P.get(i).x * P.get((i + 1) % this.P.size()).y - P.get(i).y * P.get((i + 1) % this.P.size()).x) + area;
        return Math.abs(area);
    }

    double GetCircle() {
        double circle = 0;
        for (int i = 0; i < this.P.size(); i++)
            circle = P.get(i).getDistance(P.get((i + 1) % this.P.size())) + circle;
        return circle;
    }

    double GetLineLength(int i) {
        return P.get(i).getDistance(P.get((i + 1) % this.P.size()));
    }

    boolean isCoincideLine(line l) {
        for (int i = 0; i < this.P.size(); i++)
            if (L.get(i).lineCoincide(l))
                return true;
        return false;
    }

    boolean isPointOnPoly(points p) {
        for (int i = 0; i < this.P.size(); i++)
            if (L.get(i).getDistance(p) == 0 && L.get(i).isBetween(p))
                return true;
        return false;
    }
    boolean isPointCoincideVes(points p) {
        for (int i = 0; i < this.P.size(); i++)
            if (P.get(i).coincide(p))
                return true;
        return false;
    }
    void LineCutPoly(line l) {
        Format f = new Format();
        ArrayList<points> inter = new ArrayList<points>();
        inter = this.GetIntersection(l);
        System.out.print(inter.size() + " ");
        if (inter.size() == 2) {
            for (int i = 0; i < this.P.size(); i++) {
                if(l.getK()>0) {
                    if (l.PointOnOneSide(this.P.get(i)))
                        inter.add(this.P.get(i));
                }
                else
                {
                    if (l.PointOnOneSide1(this.P.get(i)))
                        inter.add(this.P.get(i));
                }
            }
            Poly cutpoly = new Poly(inter);
            f.FormatOut(Math.min(this.GetArea() - cutpoly.GetArea(), cutpoly.GetArea()));
            System.out.print(" ");
            f.FormatOut(Math.max(this.GetArea() - cutpoly.GetArea(), cutpoly.GetArea()));
        }
    }
    ArrayList<points> GetPolyLineInter(Poly a) {
        for (int i = 0; i < this.P.size(); i++) {
            for (int j = 0; j < a.P.size(); j++)
                if (this.L.get(i).lineIntersection(a.L.get(j))) {
                    points p = new points();
                    p = L.get(i).getIntersection(a.L.get(j));
                    if (!p.isSameElemts(P)&& L.get(i).isBetween(p)) {
                        P.add(p);
                    }
                }
        }
        return P;
    }

    boolean isPolyLineCoincide(Poly a) {
        for (int i = 0; i < this.P.size(); i++) {
            for (int j = 0; j < a.P.size(); j++)
                if (this.L.get(i).SegmentCoincide(a.L.get(j)))
                    return true;
        }
        return false;
    }

    boolean IsPointInPoly(points p) {
        double sumarea = 0;
        for (int i = 0; i < this.P.size(); i++) {
            triangle t = new triangle(p, this.P.get(i), this.P.get((i + 1) % this.P.size()));
            sumarea = t.GetArea() + sumarea;
        }
        return sumarea == this.GetArea();
    }
    
    boolean isPolyVexOnPoly(Poly a) {
        for(int i=0;i<this.P.size();i++) 
            if(!a.isPointOnPoly(this.P.get(i)))
                return false;
        return true;
    }

    ArrayList<points> GetIntersection(line l) {
        ArrayList<points> inter=new ArrayList<points>();
        for (int i = this.P.size()-1; i >=0; i--) {
            if (!L.get(i).isParallel(l)) {
                points a = new points();
                a = L.get(i).getIntersection(l);
                if (!a.isSameElemts(inter)&& L.get(i).isBetween(a)) {
                    if(!(i==this.P.size()-1&&a.coincide(P.get(0))))
                        inter.add(a);
                }
            }
        }
        return inter;
    }

    boolean isPolyCoincidePoly(Poly a) {
        int count = 0;
        if (this.P.size() == a.P.size()) {
            for (int i = 0; i < this.P.size(); i++) {
                for (int j = 0; j < a.P.size(); j++) {
                    if (this.P.get(i).coincide(a.P.get(j))) {
                        count++;
                        break;
                    }
                }
            }
            return count == this.P.size();
        } else
            return false;
    }

    boolean isAllPointsInPoly(Poly a) {
        for (int i = 0; i < a.P.size(); i++)
            if (!this.IsPointInPoly(a.P.get(i)))
                return false;
        return true;
    }

    void ConnectionWithOther(Pentagon a) {
        if (a.isPentagon()) {
            this.ConnectionWithPoly(a);
        } else if (a.P.size() == 4) {
            Quadrilateral Q1 = new Quadrilateral(a.P);
            this.ConnectionWithPoly(Q1);
        } else if (a.P.size() == 3) {
            triangle t1 = new triangle(a.P);
            this.ConnectionWithPoly(t1);
        }
    }

    void ConnectionWithPoly(Poly a) {
        if (this.isPolyCoincidePoly(a)) // 重合
            System.out.print("the previous " + this.Findtype(this.P.size()) + " coincides with the following " + a.Findtype(a.P.size()));
        else if (!this.isAllPointsInPoly(a) && !a.isAllPointsInPoly(this)&&!!this.isPolyVexOnPoly(a)&&!!a.isPolyVexOnPoly(this))// 分离
            System.out.print("no overlapping area between the previous " + this.Findtype(this.P.size()) + " and the following " + a.Findtype(a.P.size()));
        else if (this.isAllPointsInPoly(a))// a全在this里
            System.out.print("the previous " + this.Findtype(this.P.size()) + " contains the following " + a.Findtype(a.P.size()));
        else if (a.isAllPointsInPoly(this))// this全在a里
            System.out.print("the previous " + this.Findtype(this.P.size()) + " is inside the following " + a.Findtype(a.P.size()));
        else if(this.isConnectWith(a)) {
            System.out.print("the previous " + this.Findtype(this.P.size()) + " is connected to the following " + a.Findtype(a.P.size()));
        }
    }

    boolean isConnectWith(Poly a) {
        ArrayList<points> inter=this.GetPolyLineInter(a);
        if(inter.get(1)==null) {
            if(this.isPointCoincideVes(inter.get(0))||a.isPointCoincideVes(inter.get(0)))
                return true;
        }
        else
            return false;
        return false;
    }

    String Findtype(int x) {
        if (x == 3)
            return "triangle";
        else if (x == 4)
            return "quadrilateral";
        else
            return "pentagon";
    }
    int isCoincideVertex(points a) {
        for(int i=0;i<this.P.size();i++) {
            if(this.P.get(i).coincide(a))
                return i;
        }
        return -1;
    }

    int onWhitchLine(points a) {
        for(int i=0;i<this.P.size();i++) {
            if(this.L.get(i).isBetween(a))
                return i;
        }
        return -1;
    }
    points Findvex(int x) {
        return this.P.get(x);
    }

    line Findline(int x) {
        return this.L.get(x);
    }
}
class Pentagon extends Poly{
    points a, b, c, d, e;
    line A = new line();
    line B = new line();
    line C = new line();
    line D = new line();
    line E = new line();

    Pentagon(points a, points b, points c, points d, points e) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
        this.e = e;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = e;
        this.E.a = e;
        this.E.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        P.add(d);
        P.add(e);        
        this.P=this.GetPoint(P);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Pentagon(ArrayList<points> p) {
        this.a = p.get(0);
        this.b = p.get(1);
        this.c = p.get(2);
        this.d = p.get(3);
        this.e = p.get(4);
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = e;
        this.E.a = e;
        this.E.b = a;
        this.P=this.GetPoint(p);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Pentagon() {

    }


    boolean isPentagon() {
        triangle a = new triangle(this.e, this.a, this.b);
        triangle b = new triangle(this.a, this.b, this.c);
        triangle c = new triangle(this.b, this.c, this.d);
        triangle d = new triangle(this.c, this.d, this.e);
        triangle e = new triangle(this.d, this.e, this.a);
        if (a.isTriangle() && b.isTriangle() && c.isTriangle() && d.isTriangle() && e.isTriangle()) {
            if (A.lineIntersection(C) || A.lineIntersection(D) || B.lineIntersection(D) || B.lineIntersection(E)
                    || C.lineIntersection(E))
                return false;
            else
                return true;
        } else
            return false;
    }

    boolean isConcave() {
        double a1, b1, a2, b2;
        for (int i = 0; i < 5; i++) {
            a1=L.get(i).b.x-L.get(i).a.x;
            b1=L.get(i).b.y-L.get(i).a.y;
            a2=L.get((i+1)%5).b.x-L.get((i+1)%5).a.x;
            b2=L.get((i+1)%5).b.y-L.get((i+1)%5).a.y;
            if (crossProduct(a1, b1, a2, b2) < 0)
                return true;
        }
        return false;

    }

    double crossProduct(double a1, double b1, double a2, double b2) {
        return a1 * b2 - b1 * a2;
    }
}
class Quadrilateral extends Poly{
    points a, b, c, d;
    line A = new line();
    line B = new line();
    line C = new line();
    line D = new line();
    Quadrilateral(points a, points b, points c, points d) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        P.add(d);
        this.P=this.GetPoint(P);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Quadrilateral(ArrayList<points> p) {
        this.a = p.get(0);
        this.b = p.get(1);
        this.c = p.get(2);
        this.d = p.get(3);
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = a;
        this.P=this.GetPoint(p);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Quadrilateral() {
    }
    boolean isQuadrilateral() {
        triangle a = new triangle(this.a, this.b, this.c);
        triangle b = new triangle(this.b, this.c, this.d);
        triangle c = new triangle(this.c, this.d, this.a);
        triangle d = new triangle(this.d, this.a, this.b);
        if (a.isTriangle() && b.isTriangle() && c.isTriangle() && d.isTriangle()) {
            points p = new points();
            if (!this.A.isParallel(this.C)) {
                p = this.A.getIntersection(this.C);
                if (this.A.isBetween(p) && this.C.isBetween(p))
                    return false;
            }
            if (!this.B.isParallel(this.D)) {
                p = this.B.getIntersection(this.D);
                if (this.B.isBetween(p) && this.D.isBetween(p))
                    return false;
            }
            return true;
        } else
            return false;
    }
    boolean isConcave() {// 凹
        triangle a = new triangle(this.a, this.b, this.c);
        triangle b = new triangle(this.b, this.c, this.d);
        triangle c = new triangle(this.c, this.d, this.a);
        triangle d = new triangle(this.d, this.a, this.b);
        if (a.GetArea() + c.GetArea() == b.GetArea() + d.GetArea())
            return false;
        else
            return true;
    }
}
class triangle extends Poly{
    points a,b,c;
    line A = new line();
    line B = new line();
    line C = new line();
    public triangle(points a, points b, points c) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }    
    }
    triangle(ArrayList<points> p) {
        this.a = p.get(0);
        this.b = p.get(1);
        this.c = p.get(2);    
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = a;
        P=p;
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    public triangle(){
        
    }
    public boolean isTriangle() {
        if (this.GetArea() != 0)
            return true;
        else
            return false;
    }
}

第二题

import java.util.Scanner;
import java.util.ArrayList;

public class Main {

    
    
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        Format P = new Format();
        P.s = input.nextLine();
        if (!P.matche()) {
            System.out.println("Wrong Format");
            return;
        }
        if (P.numberNo() == 4) {
            if (P.numberPoints() == 10) {
                Pentagon a1 = new Pentagon(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4),
                        P.getPoints(5));
                Pentagon a2 = new Pentagon(P.getPoints(6), P.getPoints(7), P.getPoints(8), P.getPoints(9),
                        P.getPoints(10));
                a1.ConnectionWithOther(a2);
            }
                else
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 5) {
            if (P.numberPoints() == 10) {
        Pentagon a1 = new Pentagon(P.getPoints(1), P.getPoints(2), P.getPoints(3), P.getPoints(4),
                        P.getPoints(5));
                Pentagon a2 = new Pentagon(P.getPoints(6), P.getPoints(7), P.getPoints(8), P.getPoints(9),
                        P.getPoints(10));
                a1.CommonArea(a2);
            } else
                System.out.println("wrong number of points");
        } else if (P.numberNo() == 6) {
            if (P.numberPoints() == 6) {
                points p = new points(P.getPoints(1));
                Pentagon a = new Pentagon(P.getPoints(2), P.getPoints(3), P.getPoints(4), P.getPoints(5),P.getPoints(6));
                if(a.isPointOnPoly(p)) {
                    System.out.println("on the "+a.Findtype(a.L.size()));
                    return;
                }
                if(a.IsPointInPoly(p))
                    System.out.println("in the "+a.Findtype(a.L.size()));
                else
                    System.out.println("outof the "+a.Findtype(a.L.size()));
            } else
                System.out.println("wrong number of points");
        }
    }
}

class Format {
    String s;
    public boolean matche() {
        String regx = "[+-]?([1-9]\\d*|0)(\\.\\d+)?";
        if (this.s.charAt(1) != ':')
            return false;
        String arr = this.s.substring(2);
        String arr1[] = arr.split(" ");
        for (int i = 0; i < arr1.length; i++) {
            String arr2[] = arr1[i].split(",");
            if (arr2.length != 2)
                return false;
            if (!arr2[0].matches(regx))
                return false;
            if (!arr2[1].matches(regx))
                return false;
        }
        return true;
    }
    public int numberNo() {
        return Integer.parseInt(this.s.split(":")[0]);
    }

    public int numberPoints() {
        String arr[] = this.s.split(" |:");
        return arr.length - 1;
    }

    public points getPoints(int index) {
        points a = new points();
        String arr[] = this.s.split(":")[1].split(" ");
        a.x = Double.parseDouble(arr[index - 1].split(",")[0]);
        a.y = Double.parseDouble(arr[index - 1].split(",")[1]);
        return a;
    }

    public void FormatOut(double x) {
        if ((x * 1e3) % 10 != 0)
            System.out.printf("%.3f", x);
        else
            System.out.print(x);
    }
    ArrayList<points> SortPoint(ArrayList<points> p){
        ArrayList<points> sort=new ArrayList<points> ();
        double sumx=0,sumy=0;
        for(int i=0;i<p.size();i++)
        {
            sumx=p.get(i).x+sumx;
            sumy=p.get(i).y+sumy;
        }
        points g=new points(sumx/p.size(),sumy/p.size());

        for(int i=0;i<p.size();i++)
            p.get(i).SetP(g);
        int index=0;
        while (p.size()!=0)
            {
            index=0;
                for(int j=0;j<p.size();j++)
                    if(p.get(j).angle<p.get(index).angle)
                        index=j;
            sort.add(p.get(index));
            p.remove(index);
            }
        return sort;
    }
}
class line {
    points a, b;

    line() {
    }

    line(points a, points b) {
        this.a = a;
        this.b = b;
    }

    public boolean isK() {
        if (this.a.x == this.b.x)
            return false;
        else
            return true;
    }

    public double getK() {
        return (this.a.y - this.b.y) / (this.a.x - this.b.x);
    }

    public double getB() {
        return this.a.y - this.a.x * this.getK();
    }

    public double getDistance(points a) {
        if (this.isK()) {
            double numerator = Math.abs(getK() * a.x - a.y + this.getB());
            double denominator = Math.sqrt(1 + Math.pow(this.getK(), 2));
            return numerator / denominator;
        } else
            return Math.abs(this.a.x - a.x);
    }

    public boolean isOnline(points a) {
        if (this.getDistance(a) == 0)
            return true;
        else
            return false;
    }

    public double getA1() {
        return this.b.y - this.a.y;
    }

    public double getB1() {
        return this.a.x - this.b.x;
    }

    public double getC1() {
        return this.a.x * this.getA1()+ this.a.y * this.getB1();
    }

    public points getIntersection(line a) {
        double A, B;
        double A1, B1, C1;
        double A2, B2, C2;
        A1 = a.getA1();
        B1 = a.getB1();
        C1 = a.getC1();
        A2 = this.getA1();
        B2 = this.getB1();
        C2 = this.getC1();
        double X, Y;
        A = (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1);
        B = (A1 * C2 - A2 * C1) / (A1 * B2 - A2 * B1);
        points d = new points();
        d.x = A;
        d.y = B;
        return d;
    }

    public boolean isParallel(line a) {
        if (this.isK() && a.isK()) {
            if (this.getK() == a.getK())
                return true;
            else
                return false;
        } else if (!this.isK() && !a.isK())
            return true;
        else
            return false;
    }

    public boolean isVertical(line a) {
        if (this.isK() && a.isK()) {
            if (this.getK() * a.getK() == -1)
                return true;
            else
                return false;
        } else if (!this.isK() && a.getK() == 0)
            return true;
        else if (this.getK() == 0 && !a.isK())
            return true;
        else
            return false;
    }

    public boolean isBetween(points a) {
        if (a.x >= Math.min(this.a.x, this.b.x) && a.x <= Math.max(this.a.x, this.b.x)
                && a.y >= Math.min(this.a.y, this.b.y) && a.y <= Math.max(this.a.y, this.b.y))
            return true;
        else
            return false;
    }

    public double lineLength() {
        return this.a.getDistance(this.b);
    }

    public boolean lineCoincide(line a) {
        if (this.isK() && a.isK()) {
            if (this.isParallel(a) && this.getB() == a.getB())
                return true;
            else
                return false;
        } else if (!this.isK() && !a.isK()) {
            if (this.a.x == a.a.x)
                return true;
            else
                return false;
        } else
            return false;
    }

    public boolean SegmentCoincide(line a) {
        boolean onLineA, onLineB, onLineC, onLineD;
        onLineA = this.a.onSameLine(a.a, a.b);//a在cd
        onLineB = this.b.onSameLine(a.a, a.b);//b在cd
        onLineC = a.a.onSameLine(this.a, this.b);//c在ab
        onLineD = a.b.onSameLine(this.a, this.b);//d在ab
        boolean coincide01 = (onLineA && onLineB) || (onLineC && onLineD);
        boolean coincide02 = (onLineB && onLineC) || (onLineA && onLineD );
        return (coincide01 || coincide02);
    }

    public boolean lineIntersection(line a) {
        if (Math.max(this.a.x, this.b.x) < Math.min(a.a.x, a.b.x)
                || Math.min(this.a.x, this.b.x) > Math.max(a.a.x, a.b.x)
                || Math.max(this.a.y, this.b.y) < Math.min(a.a.y, a.b.y)
                || Math.min(this.a.y, this.b.y) > Math.max(a.a.y, a.b.y)) {
            return false;
        }
        if (crossProduct(this.a.x - a.a.x, this.a.y - a.a.y, a.a.x - a.b.x, a.a.y - a.b.y)
                * crossProduct(this.b.x - a.a.x, this.b.y - a.a.y, a.a.x - a.b.x, a.a.y - a.b.y) > 0) {
            return false;
        }
        if (crossProduct(a.a.x - this.a.x, a.a.y - this.a.y, this.a.x - this.b.x, this.a.y - this.b.y)
                * crossProduct(a.b.x - this.a.x, a.b.y - this.a.y, this.a.x - this.b.x, this.a.y - this.b.y) > 0) {
            return false;
        }
        return true;
    }

    double crossProduct(double a1, double b1, double a2, double b2) {
        return a1 * b2 - b1 * a2;
    }
    boolean PointOnOneSide(points a) {
        if(a.x*this.getA1()+a.y*this.getB1()-this.getC1()>0)
            return true;
        else
            return false;
    }
    boolean PointOnOneSide1(points a) {
        if(a.x*this.getA1()+a.y*this.getB1()-this.getC1()<0)
            return true;
        else
            return false;
    }
}
class points {
    double x,y;
    double p,angle;
    points(){
        
    }
    points(points a){
        this.x=a.x;
        this.y=a.y;
    }
    public points(double x, double y) {
        this.x=x;
        this.y=y;
    }
    public double getDistance(points a) {
        return Math.sqrt(Math.pow(this.x-a.x,2)+Math.pow(this.y-a.y,2));
    }
    public double getSquare(points a) {
        return Math.pow(this.x-a.x,2)+Math.pow(this.y-a.y,2);
    }
    public boolean coincide(points a) {
        if(this.x==a.x&&this.y==a.y)
            return true;
        else
            return false;
    }
    public boolean onSameLine(points a,points b) {
        line l=new line(a,b);
        return l.isOnline(this)&&l.isBetween(this);
    }
    public boolean isSameElemts(ArrayList<points> P) {
        if(P.size()==0)
            return false;
        for(int i=0;i<P.size();i++)
        {
            if(this.coincide(P.get(i)))
                return true;
        }
        return false;
    }
    void SetP(points a) {
        
        this.p=Math.sqrt(Math.pow(this.x-a.x, 2)+Math.pow(this.y-a.y, 2));
        double jiaodu=Math.atan2(y-a.y, x-a.x);
        if (jiaodu<0) 
            this.angle=2*Math.PI+jiaodu;
        else
            this.angle=jiaodu;
    }
}

class Poly {
    ArrayList<points> P = new ArrayList<points>();
    ArrayList<line> L = new ArrayList<line>();
    Poly(){
        
    }
    Poly(ArrayList<points> p) {        
        this.P=this.GetPoint(p);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    ArrayList<points> GetPoint(ArrayList<points> p2) {
        ArrayList<points> P=new ArrayList<points>();
        for(int i=0;i<p2.size();i++) 
            for(int j=i+1;j<p2.size();) {
                if(p2.get(i).coincide(p2.get(j)))
                        p2.remove(j);
                else
                        j++;
            }
        for(int i=0;i<p2.size();i++) {
            if(!p2.get(i).onSameLine(p2.get((i+p2.size()-1)%p2.size()), p2.get((i+p2.size()+1)%p2.size())))
                    P.add(p2.get(i));
        }
        return P;
    }
    double GetArea() {
        double area = 0;
        for (int i = 0; i < this.P.size(); i++)
            area = 0.5 * (P.get(i).x * P.get((i + 1) % this.P.size()).y - P.get(i).y * P.get((i + 1) % this.P.size()).x) + area;
        return Math.abs(area);
    }

    double GetCircle() {
        double circle = 0;
        for (int i = 0; i < this.P.size(); i++)
            circle = P.get(i).getDistance(P.get((i + 1) % this.P.size())) + circle;
        return circle;
    }

    double GetLineLength(int i) {
        return P.get(i).getDistance(P.get((i + 1) % this.P.size()));
    }

    boolean isCoincideLine(line l) {
        for (int i = 0; i < this.P.size(); i++)
            if (L.get(i).lineCoincide(l))
                return true;
        return false;
    }

    boolean isPointOnPoly(points p) {
        for (int i = 0; i < this.P.size(); i++)
            if (L.get(i).getDistance(p) == 0 && L.get(i).isBetween(p))
                return true;
        return false;
    }
    boolean isPointCoincideVes(points p) {
        for (int i = 0; i < this.P.size(); i++)
            if (P.get(i).coincide(p))
                return true;
        return false;
    }
    void LineCutPoly(line l) {
        Format f = new Format();
        ArrayList<points> inter = new ArrayList<points>();
        inter = this.GetIntersection(l);
        System.out.print(inter.size() + " ");
        if (inter.size() == 2) {
            for (int i = 0; i < this.P.size(); i++) {
                if(l.getK()>0) {
                    if (l.PointOnOneSide(this.P.get(i)))
                        inter.add(this.P.get(i));
                }
                else
                {
                    if (l.PointOnOneSide1(this.P.get(i)))
                        inter.add(this.P.get(i));
                }
            }
            Poly cutpoly = new Poly(inter);
            f.FormatOut(Math.min(this.GetArea() - cutpoly.GetArea(), cutpoly.GetArea()));
            System.out.print(" ");
            f.FormatOut(Math.max(this.GetArea() - cutpoly.GetArea(), cutpoly.GetArea()));
        }
    }
    ArrayList<points> GetPolyLineInter(Poly a) {
        ArrayList<points> inter = new ArrayList<points>();
        for (int i = 0; i < this.P.size(); i++) {
            for (int j = 0; j < a.P.size(); j++)
                if (this.L.get(i).lineIntersection(a.L.get(j))) {
                    points p = new points();
                    p = L.get(i).getIntersection(a.L.get(j));
                    if (!p.isSameElemts(inter) && L.get(i).isBetween(p)) {
                        inter.add(p);
                    }
                }
        }
        return inter;
    }

    boolean isPolyLineCoincide(Poly a) {
        for (int i = 0; i < this.P.size(); i++) {
            for (int j = 0; j < a.P.size(); j++)
                if (this.L.get(i).SegmentCoincide(a.L.get(j)))
                    return true;
        }
        return false;
    }

    boolean IsPointInPoly(points p) {
        double sumarea = 0;
        for (int i = 0; i < this.P.size(); i++) {
            triangle t = new triangle(p, this.P.get(i), this.P.get((i + 1) % this.P.size()));
            sumarea = t.GetArea() + sumarea;
        }
        return sumarea == this.GetArea();
    }
    
    boolean isPolyVexOnPoly(Poly a) {
        for(int i=0;i<this.P.size();i++) 
            if(!a.isPointOnPoly(this.P.get(i)))
                return false;
        return true;
    }

    ArrayList<points> GetIntersection(line l) {
        ArrayList<points> inter=new ArrayList<points>();
        for (int i = this.P.size()-1; i >=0; i--) {
            if (!L.get(i).isParallel(l)) {
                points a = new points();
                a = L.get(i).getIntersection(l);
                if (!a.isSameElemts(inter)&& L.get(i).isBetween(a)) {
                    if(!(i==this.P.size()-1&&a.coincide(P.get(0))))
                        inter.add(a);
                }
            }
        }
        return inter;
    }

    boolean isPolyCoincidePoly(Poly a) {
        int count = 0;
        if (this.P.size() == a.P.size()) {
            for (int i = 0; i < this.P.size(); i++) {
                for (int j = 0; j < a.P.size(); j++) {
                    if (this.P.get(i).coincide(a.P.get(j))) {
                        count++;
                        break;
                    }
                }
            }
            return count == this.P.size();
        } else
            return false;
    }

    boolean isAllPointsInPoly(Poly a) {
        for (int i = 0; i < a.P.size(); i++)
            if (!this.IsPointInPoly(a.P.get(i)))
                return false;
        return true;
    }

    void ConnectionWithOther(Pentagon a) {
        if (a.isPentagon()) {
            this.ConnectionWithPoly(a);
        } else if (a.P.size() == 4) {
            Quadrilateral Q1 = new Quadrilateral(a.P);
            this.ConnectionWithPoly(Q1);
        } else if (a.P.size() == 3) {
            triangle t1 = new triangle(a.P);
            this.ConnectionWithPoly(t1);
        }
    }

    boolean isAllPointsNotInPoly(Poly a) {
        for (int i = 0; i < a.P.size(); i++)
            if (this.IsPointInPoly(a.P.get(i)))
                return false;
        return true;
    }
     void ConnectionWithPoly(Poly a) {
        ArrayList<points> inter=new ArrayList<points>();
        inter=this.GetPolyLineInter(a);
        if (this.isPolyCoincidePoly(a)) // 重合
            {
                System.out.print("the previous " + this.Findtype(this.P.size()) + " coincides with the following "
                    + a.Findtype(a.P.size()));
                return ;
            }
        if (this.isAllPointsNotInPoly(a) && a.isAllPointsNotInPoly(this)) {
            System.out.print("no overlapping area between the previous " + this.Findtype(this.P.size())
                    + " and the following " + a.Findtype(a.P.size()));
        }
        else if (this.isAllPointsInPoly(a))// a全在this里
            System.out.print("the previous " + this.Findtype(this.P.size()) + " contains the following "
                    + a.Findtype(a.P.size()));
        else if (a.isAllPointsInPoly(this))// this全在a里
            System.out.print("the previous " + this.Findtype(this.P.size()) + " is inside the following "
                    + a.Findtype(a.P.size()));
        else if(this.isConnectWith(a))
            System.out.print("the previous " + this.Findtype(this.P.size()) + " is connected to the following "
                    + a.Findtype(a.P.size()));
        else
            System.out.print("the previous " + this.Findtype(this.P.size()) + " is interlaced with the following "
                    + a.Findtype(a.P.size()));
    }
int ConnectionWithPolyType(Poly a) {
        ArrayList<points> inter=new ArrayList<points>();
        inter=this.GetPolyLineInter(a);
        if (this.isPolyCoincidePoly(a)) // 重合
            return 1;
        if (this.isAllPointsNotInPoly(a) && a.isAllPointsNotInPoly(this))// 分离
            return 2;
        else if (this.isAllPointsInPoly(a))// a全在this里
            return 3;
        else if (a.isAllPointsInPoly(this))// this全在a里
            return 4;
        else if(this.isConnectWith(a))
            return 5;
        else
            return 6;
    }
    boolean isConnectWith(Poly a) {
        ArrayList<points> inter = this.GetPolyLineInter(a);
        if (inter.size()==1) {
            for(int i=0;i<this.P.size();i++) {
                if(this.P.get(i).coincide(inter.get(0)))
                    continue;
                if(a.IsPointInPoly(this.P.get(i)))
                    return false;
            }
            return true;
        } else if (inter.size()==2) {
            for(int i=0;i<this.P.size();i++) {
                if(this.P.get(i).coincide(inter.get(0))||this.P.get(i).coincide(inter.get(1)))
                    continue;
                if(a.IsPointInPoly(this.P.get(i)))
                    return false;
            }
            return true;
        } else
            return false;
    }
    void CommonArea(Pentagon a) {
        Format p=new Format();
        ArrayList<points> inter = this.GetPolyLineInter(a);
        if(this.ConnectionWithPolyType(a)==1||this.ConnectionWithPolyType(a)==3)
            System.out.print(a.GetArea());
        else if(this.ConnectionWithPolyType(a)==4)
            System.out.print(this.GetArea());
        else {
            for(int i=0;i<this.P.size();i++) {
                if(a.IsPointInPoly(this.P.get(i))&&!this.P.get(i).isSameElemts(inter)) {
                    inter.add(P.get(i));
                }
            }
            for(int i=0;i<a.P.size();i++) {
                if(this.IsPointInPoly(a.P.get(i))&&!a.P.get(i).isSameElemts(inter)) {
                    inter.add(a.P.get(i));
                }
            }
            inter=p.SortPoint(inter);
            Poly poly=new Poly(inter);
            p.FormatOut(poly.GetArea());
            /*for(int i=0;i<inter.size();i++) {
                System.out.print(inter.get(i).x+" "+inter.get(i).y+"\n");
            }*/
            
        }
    }
    String Findtype(int x) {
        if (x == 3)
            return "triangle";
        else if (x == 4)
            return "quadrilateral";
        else
            return "pentagon";
    }
    int isCoincideVertex(points a) {
        for(int i=0;i<this.P.size();i++) {
            if(this.P.get(i).coincide(a))
                return i;
        }
        return -1;
    }

    int onWhitchLine(points a) {
        for(int i=0;i<this.P.size();i++) {
            if(this.L.get(i).isBetween(a))
                return i;
        }
        return -1;
    }
    points Findvex(int x) {
        return this.P.get(x);
    }

    line Findline(int x) {
        return this.L.get(x);
    }
}
class Pentagon extends Poly{
    points a, b, c, d, e;
    line A = new line();
    line B = new line();
    line C = new line();
    line D = new line();
    line E = new line();

    Pentagon(points a, points b, points c, points d, points e) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
        this.e = e;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = e;
        this.E.a = e;
        this.E.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        P.add(d);
        P.add(e);        
        this.P=this.GetPoint(P);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Pentagon(ArrayList<points> p) {
        this.a = p.get(0);
        this.b = p.get(1);
        this.c = p.get(2);
        this.d = p.get(3);
        this.e = p.get(4);
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = e;
        this.E.a = e;
        this.E.b = a;
        this.P=this.GetPoint(p);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Pentagon() {

    }


    boolean isPentagon() {
        triangle a = new triangle(this.e, this.a, this.b);
        triangle b = new triangle(this.a, this.b, this.c);
        triangle c = new triangle(this.b, this.c, this.d);
        triangle d = new triangle(this.c, this.d, this.e);
        triangle e = new triangle(this.d, this.e, this.a);
        if (a.isTriangle() && b.isTriangle() && c.isTriangle() && d.isTriangle() && e.isTriangle()) {
            if (A.lineIntersection(C) || A.lineIntersection(D) || B.lineIntersection(D) || B.lineIntersection(E)
                    || C.lineIntersection(E))
                return false;
            else
                return true;
        } else
            return false;
    }

    boolean isConcave() {
        double a1, b1, a2, b2;
        for (int i = 0; i < 5; i++) {
            a1=L.get(i).b.x-L.get(i).a.x;
            b1=L.get(i).b.y-L.get(i).a.y;
            a2=L.get((i+1)%5).b.x-L.get((i+1)%5).a.x;
            b2=L.get((i+1)%5).b.y-L.get((i+1)%5).a.y;
            if (crossProduct(a1, b1, a2, b2) < 0)
                return true;
        }
        return false;

    }

    double crossProduct(double a1, double b1, double a2, double b2) {
        return a1 * b2 - b1 * a2;
    }
}
class Quadrilateral extends Poly{
    points a, b, c, d;
    line A = new line();
    line B = new line();
    line C = new line();
    line D = new line();
    Quadrilateral(points a, points b, points c, points d) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        P.add(d);
        this.P=this.GetPoint(P);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Quadrilateral(ArrayList<points> p) {
        this.a = p.get(0);
        this.b = p.get(1);
        this.c = p.get(2);
        this.d = p.get(3);
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = d;
        this.D.a = d;
        this.D.b = a;
        this.P=this.GetPoint(p);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    Quadrilateral() {
    }
    boolean isQuadrilateral() {
        triangle a = new triangle(this.a, this.b, this.c);
        triangle b = new triangle(this.b, this.c, this.d);
        triangle c = new triangle(this.c, this.d, this.a);
        triangle d = new triangle(this.d, this.a, this.b);
        if (a.isTriangle() && b.isTriangle() && c.isTriangle() && d.isTriangle()) {
            points p = new points();
            if (!this.A.isParallel(this.C)) {
                p = this.A.getIntersection(this.C);
                if (this.A.isBetween(p) && this.C.isBetween(p))
                    return false;
            }
            if (!this.B.isParallel(this.D)) {
                p = this.B.getIntersection(this.D);
                if (this.B.isBetween(p) && this.D.isBetween(p))
                    return false;
            }
            return true;
        } else
            return false;
    }
    boolean isConcave() {// 凹
        triangle a = new triangle(this.a, this.b, this.c);
        triangle b = new triangle(this.b, this.c, this.d);
        triangle c = new triangle(this.c, this.d, this.a);
        triangle d = new triangle(this.d, this.a, this.b);
        if (a.GetArea() + c.GetArea() == b.GetArea() + d.GetArea())
            return false;
        else
            return true;
    }
}
class triangle extends Poly{
    points a,b,c;
    line A = new line();
    line B = new line();
    line C = new line();
    public triangle(points a, points b, points c) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = a;
        P.add(a);
        P.add(b);
        P.add(c);
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }    
    }
    triangle(ArrayList<points> p) {
        this.a = p.get(0);
        this.b = p.get(1);
        this.c = p.get(2);    
        this.A.a = a;
        this.A.b = b;
        this.B.a = b;
        this.B.b = c;
        this.C.a = c;
        this.C.b = a;
        P=p;
        for(int i=0;i<P.size();i++)
        {
            line l=new line(P.get(i),P.get((i+1)%P.size()));
            L.add(l);
        }
    }
    public triangle(){
        
    }
    public boolean isTriangle() {
        if (this.GetArea() != 0)
            return true;
        else
            return false;
    }
}

 

 

 

 

 

 

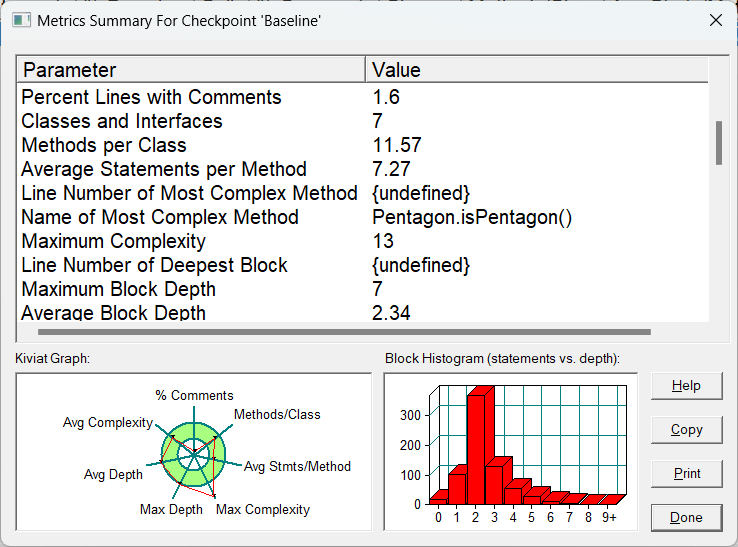
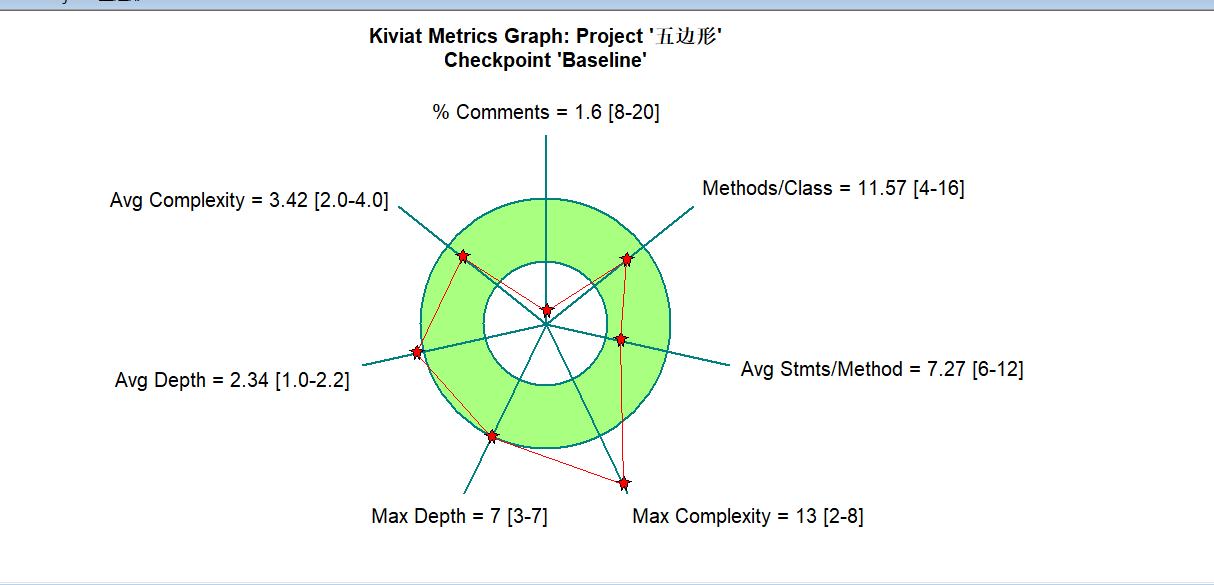
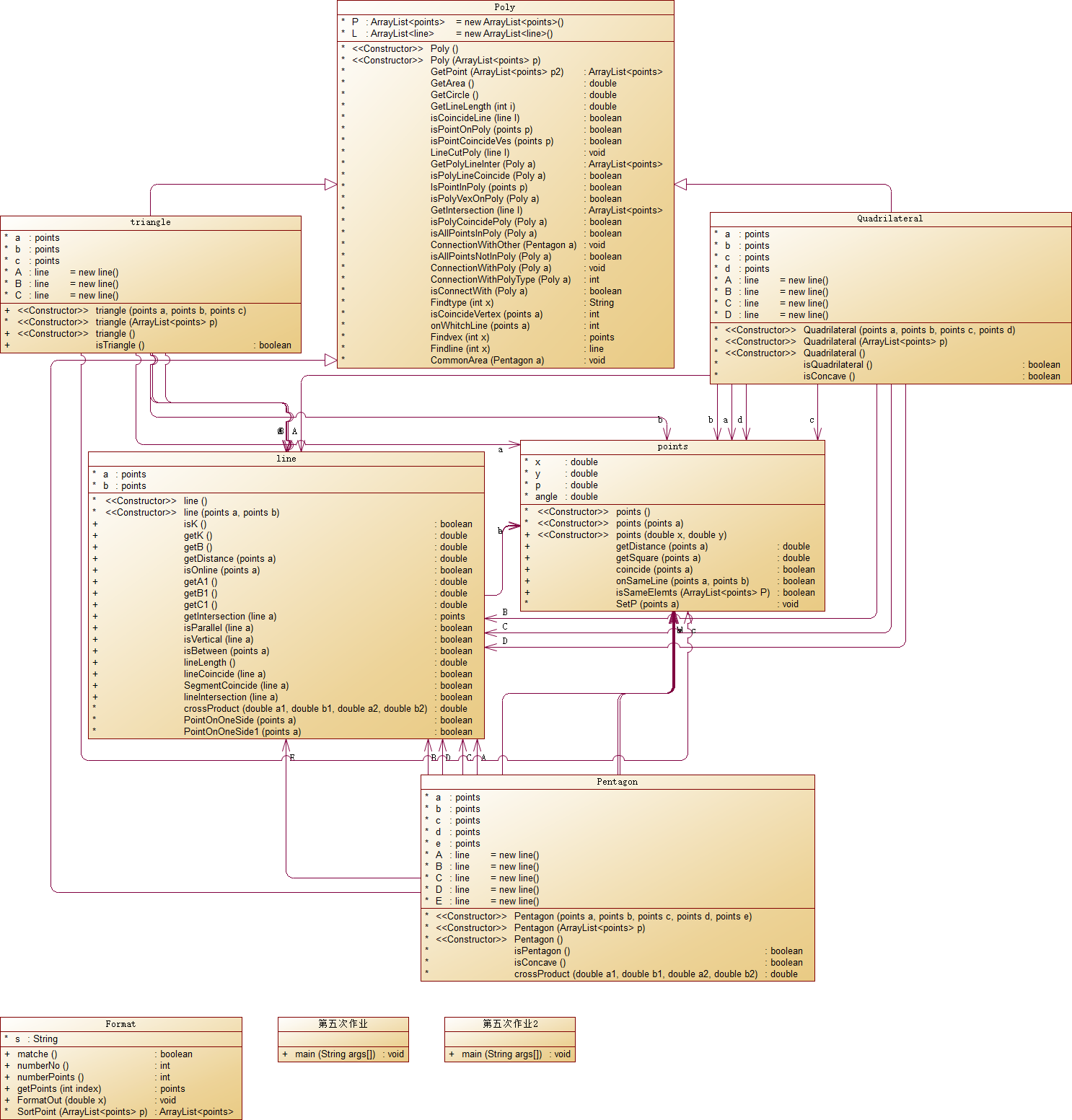
五边形题目难度是所有图形类题目中最大的,特别是第二道题,在判断多边形之间的关系中确实难住我很长时间,在使用父类后代码的复杂度有了明显的下降,其中也有很大一部分的原因是算法的优化,即便是修改优化了部分代码,但是依旧存在复杂度较高的方法,与四边形一样,都是在判断输入的多边形是否是某一特定的多边形时复杂度高,在多边形父类里我也没有实现该功能代码.

期中考试:

• 设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format

• 设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息，输出格式如下：

    ```
        The line's color is:颜色值
        The line's begin point's Coordinate is:
        (x1,y1)
        The line's end point's Coordinate is:
        (x2,y2)
        The line's length is:长度值
    ```
  

   

  其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。

    设计类图如下图所示。
  

   

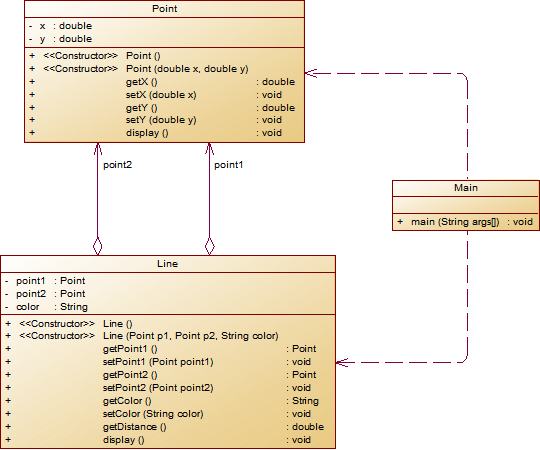
** 题目要求：在主方法中定义一条线段对象，从键盘输入该线段的起点坐标与终点坐标以及颜色，然后调用该线段的display()方法进行输出。**

 

import java.util.*;
public class Main {

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        double x1,y1,x2,y2;
        x1=input.nextDouble();
        y1=input.nextDouble();
        x2=input.nextDouble();
        y2=input.nextDouble();
        String color=input.next();
        if(x1<=0|x1>200|x2<=0|x2>200|y1<=0|y1>200|y2<=0|y2>200)
        {
            System.out.print("Wrong Format");
            return ;
        }
        Point p1=new Point(x1,y1);
        Point p2=new Point(x2,y2);
        Line l=new Line(p1,p2,color);
        l.display();
    }

}
class Line {
    private Point point1;
    private Point point2;
    private String color;
    Line(){
        
    }
    Line(Point p1,Point p2,String color){
        this.point1=p1;
        this.point2=p2;
        this.setColor(color);
    }
    public Point getPoint1() {
        return point1;
    }
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    public Point getPoint2() {
        return point2;
    }
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    public double getDistance() {
        return Math.sqrt(Math.pow(this.point1.getX()-this.point2.getX(), 2)+Math.pow(this.point1.getY()-this.point2.getY(), 2));
    }
    public void display() {
        System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:"); 
        this.point1.display();
        System.out.println("The line's end point's Coordinate is:"); 
        this.point2.display();   
        System.out.println("The line's length is:"+String.format("%.2f",this.getDistance())); 

    }
}
class Point {
    private double x;
    private double y;
    Point(){
        
    }
    Point(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double getX() {
        return x;
    }
    public void setX(double x) {
        this.x = x;
    }
    public double getY() {
        return y;
    }
    public void setY(double y) {
        this.y = y;
    }
    public void display() {
        System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")");
    }
}

 

 

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

• 对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
• 再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
• 在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。示例代码如下：

        element = p1;//起点Point
        element.display();
        
        element = p2;//终点Point
        element.display();
        
        element = line;//线段
        element.display();
        
        element = plane;//面
        element.display();
  

   
  类结构如下图所示。

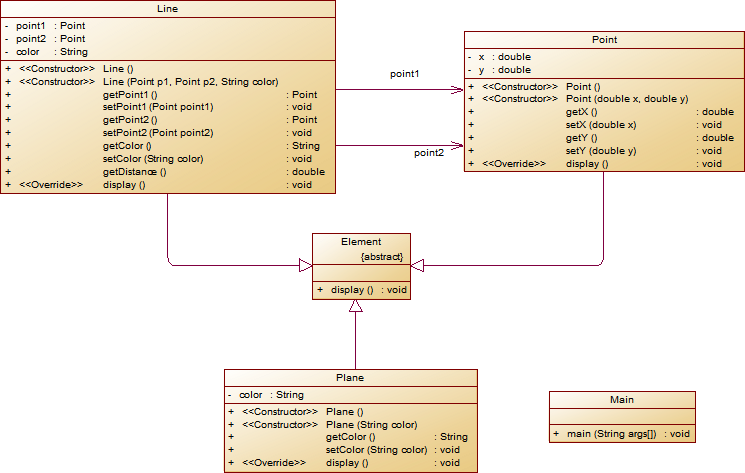
其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。

 

import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        double x1, y1, x2, y2;
        x1 = input.nextDouble();
        y1 = input.nextDouble();
        x2 = input.nextDouble();
        y2 = input.nextDouble();
        String color = input.next();
        if (x1 <= 0 | x1 > 200 | x2 <= 0 | x2 > 200 | y1 <= 0 | y1 > 200 | y2 <= 0 | y2 > 200) {
            System.out.print("Wrong Format");
            return;
        }
        Point p1 = new Point(x1, y1);
        Point p2 = new Point(x2, y2);
        Line line = new Line(p1, p2, color);
        Plane plane = new Plane(color);
        Element element;
        element = p1;// 起点Point
        element.display();

        element = p2;// 终点Point
        element.display();

        element = line;// 线段
        element.display();

        element = plane;// 面
        element.display();

    }

}
abstract class Element {
    public abstract void display();
}
class Plane extends Element{
    private String color;
    Plane(){
        
    }
    Plane(String color){
        this.color=color;
    }
    @Override
    public void display() {
        // TODO 自动生成的方法存根
        System.out.print("The Plane's color is:"+this.getColor());
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    
}
class Line extends Element{
    private Point point1;
    private Point point2;
    private String color;
    Line(){
        
    }
    Line(Point p1,Point p2,String color){
        this.point1=p1;
        this.point2=p2;
        this.setColor(color);
    }
    public Point getPoint1() {
        return point1;
    }
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    public Point getPoint2() {
        return point2;
    }
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    public double getDistance() {
        return Math.sqrt(Math.pow(this.point1.getX()-this.point2.getX(), 2)+Math.pow(this.point1.getY()-this.point2.getY(), 2));
    }
    public void display() {
        System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:"); 
        this.point1.display();
        System.out.println("The line's end point's Coordinate is:"); 
        this.point2.display();   
        System.out.println("The line's length is:"+String.format("%.2f",this.getDistance())); 

    }
}
class Point extends Element{
    private double x;
    private double y;
    Point(){
        
    }
    Point(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double getX() {
        return x;
    }
    public void setX(double x) {
        this.x = x;
    }
    public double getY() {
        return y;
    }
    public void setY(double y) {
        this.y = y;
    }
    public void display() {
        System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")");
    }
}

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

• 在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
• 增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
• 在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
  • 1：向容器中增加Point对象
  • 2：向容器中增加Line对象
  • 3：向容器中增加Plane对象
  • 4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
  • 0：输入结束
  示例代码如下：

     choice = input.nextInt();
      while(choice != 0) {
          switch(choice) {
          case 1://insert Point object into list 
            ...
              break;
          case 2://insert Line object into list
              ...
              break;
          case 3://insert Plane object into list
              ...
              break;
          case 4://delete index - 1 object from list
              int index = input.nextInt();
              ...
          }
          choice = input.nextInt();
      }
  

   
  输入结束后，按容器中的对象顺序分别调用每个对象的display()方法进行输出。
  类图如下所示：

 

 

 

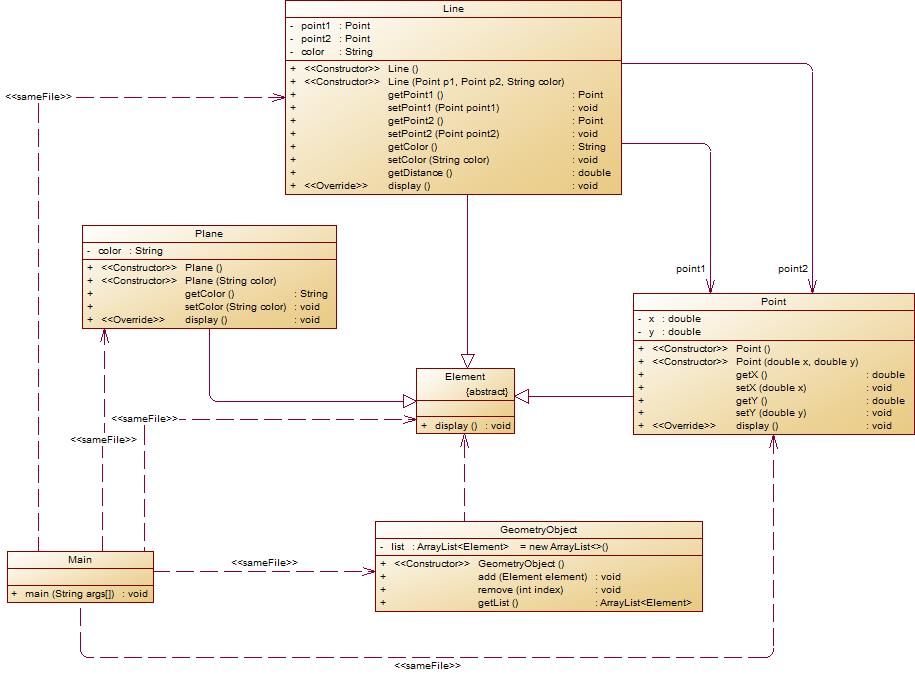
import java.util.*;
import java.util.ArrayList;
public class Main {

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        double x1, y1, x2, y2;
        String color;
        GeometryObject geometryobject=new GeometryObject();
        int choice = input.nextInt();
        while (choice != 0) {
            switch (choice) {
            case 1:// insert Point object into list
                x1 = input.nextDouble();
                y1 = input.nextDouble();
                if (x1 <= 0 | x1 > 200 | y1 <= 0 | y1 > 200) {
                    System.out.print("Wrong Format");
                    return;
                }
                Point p = new Point(x1, y1);
                geometryobject.add(p);
                break;
            case 2:// insert Line object into list
                x1 = input.nextDouble();
                y1 = input.nextDouble();
                x2 = input.nextDouble();
                y2 = input.nextDouble();
                color = input.next();
                if (x1 <= 0 | x1 > 200 | y1 <= 0 | y1 > 200|x2 <= 0 | x2 > 200 | y2 <= 0 | y2 > 200) {
                    System.out.print("Wrong Format");
                    return;
                }
                Point p1 = new Point(x1, y1);
                Point p2 = new Point(x2, y2);
                Line line=new Line(p1,p2,color);
                geometryobject.add(line);
                break;
            case 3:// insert Plane object into list
                color = input.next();
                Plane plane=new Plane(color);
                geometryobject.add(plane);
                break;
            case 4:// delete index - 1 object from list
                int index = input.nextInt();
                if(index<1||index>geometryobject.list.size())
                    break;
                else
                    geometryobject.remove(index);
            }
            choice = input.nextInt();
        }

        for(int i=0;i<geometryobject.list.size();i++)
            geometryobject.list.get(i).display();
    }

}
class GeometryObject {
    ArrayList<Element> list= new ArrayList<Element>();
    GeometryObject(){
        
    }
    public void add(Element element) {
        list.add(element);
    }
    public void remove(int index) {
        list.remove(index-1);
    }
    public ArrayList<Element> getList(){
        return list;
    }
}
class Point extends Element{
    private double x;
    private double y;
    Point(){
        
    }
    Point(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double getX() {
        return x;
    }
    public void setX(double x) {
        this.x = x;
    }
    public double getY() {
        return y;
    }
    public void setY(double y) {
        this.y = y;
    }
    public void display() {
        System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")");
    }
}
abstract class Element {
    public abstract void display();
}
class Plane extends Element{
    private String color;
    Plane(){
        
    }
    Plane(String color){
        this.color=color;
    }
    @Override
    public void display() {
        // TODO 自动生成的方法存根
        System.out.println("The Plane's color is:"+this.getColor());
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    
}
class Line extends Element{
    private Point point1;
    private Point point2;
    private String color;
    Line(){
        
    }
    Line(Point p1,Point p2,String color){
        this.point1=p1;
        this.point2=p2;
        this.setColor(color);
    }
    public Point getPoint1() {
        return point1;
    }
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    public Point getPoint2() {
        return point2;
    }
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    public double getDistance() {
        return Math.sqrt(Math.pow(this.point1.getX()-this.point2.getX(), 2)+Math.pow(this.point1.getY()-this.point2.getY(), 2));
    }
    public void display() {
        System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:"); 
        this.point1.display();
        System.out.println("The line's end point's Coordinate is:"); 
        this.point2.display();   
        System.out.println("The line's length is:"+String.format("%.2f",this.getDistance())); 

    }
}

题目难度较低,没什么好说的,主要目的就是检查我们前半学期的学习成果

三.踩坑心得

四边形:

判断多边形是否为四边形需要满足一下条件,相邻的边不共线,不相邻的边没有交点,但是我在判断线段是否存在交点的方法里面最开始使用两条直线有交点,并且交点的位置在两个线段之间,结果就是会存在测试点过不去,最后从网上找到了使用向量的叉乘来判断两条线段是否有交点

public boolean lineIntersection(line a) {
        if (Math.max(this.a.x, this.b.x) < Math.min(a.a.x, a.b.x)
                || Math.min(this.a.x, this.b.x) > Math.max(a.a.x, a.b.x)
                || Math.max(this.a.y, this.b.y) < Math.min(a.a.y, a.b.y)
                || Math.min(this.a.y, this.b.y) > Math.max(a.a.y, a.b.y)) {
            return false;
        }
        if (crossProduct(this.a.x - a.a.x, this.a.y - a.a.y, a.a.x - a.b.x, a.a.y - a.b.y)
                * crossProduct(this.b.x - a.a.x, this.b.y - a.a.y, a.a.x - a.b.x, a.a.y - a.b.y) > 0) {
            return false;
        }
        if (crossProduct(a.a.x - this.a.x, a.a.y - this.a.y, this.a.x - this.b.x, this.a.y - this.b.y)
                * crossProduct(a.b.x - this.a.x, a.b.y - this.a.y, this.a.x - this.b.x, this.a.y - this.b.y) > 0) {
            return false;
        }
        return true;
    }

假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y

输入的四个点构成三角形的情况,题目上虽然给出了提示,但是很难看懂,尤其是x y x s,这一条虽然这种情况正常看下来是不符合三角形的,但是题目把他加上了

最后是判断点是否在四边形内部,一开始我写的代码虽然通过了测试点,但是我把代码放入五边形的时候代码就无法通过了,最后还是没有使用射线法判断,而是用了面积法

五边形:

由于五边形的点数量有点多,最好是使用ArrayList来存放点或者边,最后通过循环来调取就可以

线段交点问题同四边形,也是写到五边形的时候才发现最开始的方法不够完善

选项4中,最麻烦的情况就是交错,但是我们可以不去有意的判断,直接除了其他情况剩余的就是交错

选项5中最不好想的就是如何计算,也就是算法,我们只需要把两个多边形的交点以及前一个多边形在后一个多边形里的顶点以及后一个多边形在前一个多边形里的顶点放一起,进行排序,就可以得到要求的面积了

 ArrayList<points> SortPoint(ArrayList<points> p){
        ArrayList<points> sort=new ArrayList<points> ();
        double sumx=0,sumy=0;
        for(int i=0;i<p.size();i++)
        {
            sumx=p.get(i).x+sumx;
            sumy=p.get(i).y+sumy;
        }
        points g=new points(sumx/p.size(),sumy/p.size());

        for(int i=0;i<p.size();i++)
            p.get(i).SetP(g);
        int index=0;
        while (p.size()!=0)
            {
            index=0;
                for(int j=0;j<p.size();j++)
                    if(p.get(j).angle<p.get(index).angle)
                        index=j;
            sort.add(p.get(index));
            p.remove(index);
            }
        return sort;
    }

期中考试:

格式容易出错,算法和结构很简单

四.改进建议

　　由于我在写第五题时写了一个点的排序算法,这个算法可以应用到前面题目的代码,可以再精简一下,另外可以在多边形类里加上判断是什么图形的方法,但是一直没有思路,最近从别人那学习到了可以使用向量求夹角然后算出来总的内角和度数来判断,以后可以再次更新一下代码.输入的五个点如果不能组成五边形,而是三角形的判断虽然可以执行,但是思路上应该还可以继续改进.对于期中考试来说,难度远远比不上之前写的大作业,,主要还是看清类图,注意格式的输出就好了

五.总结

　　经过这几周的学习总算是学到了Java中非常重要一个概念继承.继承就是子类继承父类的特征和行为，使得子类对象（实例）具有父类的属性和方法，或子类从父类继承方法，使得子类具有父类相同的行为。继承的运用可以进一步缩短代码长度,可以提取子类中某些共有的方法放入父类,但是直到目前为止我还是没有完全熟练掌握继承的运用,在这一方面还有待精进.同时还有针对题目中的问题,如何把判断某一多边形是哪种特定的多边形的算法依旧没有进行有效的修改,这也是有必要在将来需要继续思考的地方.