容斥原理学习笔记

容斥原理：

　　转载自：https://blog.csdn.net/love20165104027/article/details/81366047

　　计算几个集合并集的大小，计算单个元素的集合大小减去两个集合的相交的部分，加上三个集合相交的部分

　　减去四个集合相交的部分，一直到所有集合相交的部分；(将可能发生重叠的事情进行不重复的统计)

　　现在有n件事情，并且每一件对于答案都有着贡献，但是这n件事情可能会发生重叠，容斥原理的作用就在于不重复的统计

　　所有对答案有着贡献的情况的值,具体实现如图所示

　　

 

 

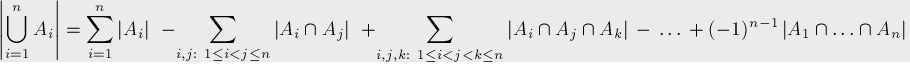
　　当然也可以将容斥原理表示的更加仔细一点：

　　

 

 

 

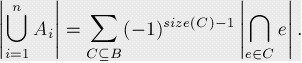
容斥原理的应用：

　   1.概率论：统计发生一件事情的概率，减去发生两件事情的概率加上发生三件事情的概率......

　　2.排列组合：统计由0~9构成的数列中首位大于1以及末尾小于8的数列的个数；（数列的限制分为了可能会造成重合的两种情况）

　　3.（0,1,2）序列问题：长度为n的由数字0,1,2组成的序列，要求每个数字至少出现一次，求这种序列的个数

　　　　我们转向它的逆问题，即所有的数字均不出现的序列，这样我们就可以用容斥原理求出不出现0的序列种树，不出现1的序列种数以此类推 

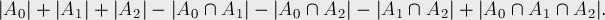              公式最终如图所示。

 

　　　　并且这道题告诉我们的是容斥原理会与原问题的更简单的逆问题相结合：方程正整数解,区间内与n互素的数就是容斥原理与逆问题的应用；

　　4.和睦数三元组的个数问题

       给出一个整数 。选出a, b, c (其中2<=a<b<c<=n)，组成和睦三元组，即：

        或者满足 ，  ， 

·　　或者满足

　　首先，我们考虑它的逆问题：也就是不和睦三元组的个数。

　　然后，我们可以发现，在每个不和睦三元组的三个元素中，我们都能找到正好两个元素满足：它与一个元素互素，并且与另一个元素不互素。

　　所以，我们只需枚举2到n的所有数，将每个数的与其互素的数的个数和与其不互素的数的个数相乘，最后求和并除以2，就是要求的逆问题的答案。

　　现在我们要考虑这个问题，如何求与2到n这些数互素（不互素）的数的个数。虽然求解与一个数互素数的个数的解法在前面已经提到过了，但在此并不合适，因为　　现在要求2到n所有数的结果，分别求解显然效率太低。

　　所以，我们需要一个更快的算法，可以一次算出2到n所有数的结果。

　　在这里，我们可以使用改进的埃拉托色尼筛法。

·　　首先，对于2到n的所有数，我们要知道构成它的素数中是否有次数大于1的，为了应用容斥原理，我们还有知道它们由多少种不同的素数构成。

　　对于这个问题，我们定义数组deg[i]：表示i由多少种不同素数构成，以及good[i]：取值true或false，表示i包含素数的次数小于等于1是否成立。

　　再利用埃拉托色尼筛法，在遍历到某个素数i时，枚举它在2到n范围内的所有倍数，更新这些倍数的deg[]值，如果有倍数包含了多个i，那么就把这个倍数的good[]值　　赋为false。

·　　然后，利用容斥原理，求出2到n每个数的cnt[i]：在2到n中不与i互素的数的个数。

　　回想容斥原理的公式，它所求的集合是不会包含重复元素的。也就是如果这个集合包含的某个素数多于一次，它们不应再被考虑。

　　所以只有当一个数i满足good[i]=true时，它才会被用于容斥原理。枚举i的所有倍数i*j，那么对于i*j，就有N/i个与i*j同样包含i（素数集合）的数。将这些结果进行加　　　减，符号由deg[i]（素数集合的大小）决定。如果deg[i]为奇数，那么我们要用加号，否则用减号。