P1174 打砖块

P1174 打砖块

小红很喜欢玩一个叫打砖块的游戏，这个游戏的规则如下：

在刚开始的时候，有 n 行 m 列的砖块，小红有 k 发子弹。小红每次可以用一发子弹，打碎某一列当前处于这一列最下面的那块砖，并且得到相应的得分。（如图所示）

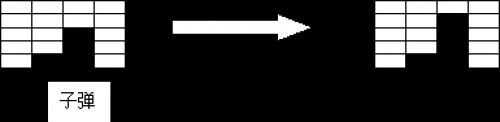
某些砖块在打碎以后，还可能将得到一发子弹的奖励。最后当所有的砖块都打碎了，或者小红没有子弹了，游戏结束。

小红在游戏开始之前，就已经知道每一块砖在打碎以后的得分，并且知道能不能得到一发奖励的子弹。小红想知道在这次游戏中她可能的最大得分，可是这个问题对于她来说太难了，你能帮帮她吗？

输入格式

第一行有 3 个正整数，n,m,k。表示开始的时候，有 n 行 m 列的砖块，小红有 k 发子弹。

接下来有 n 行，每行的格式如下：

f1 c1 f2 c2 f3 c3⋯fm c

其中 fi​ 为正整数，表示这一行的第 i 列的砖，在打碎以后的得分。ci 为一个字符，只有两种可能，Y 或者 N。Y 表示有一发奖励的子弹，N 表示没有。

所有的数与字符之间用一个空格隔开，行末没有多余的空格。

输出格式

仅一个正整数，表示最大的得分。

输入输出样例

输入 #1

3 4 2
9 N 5 N 1 N 8 N
5 N 5 Y 5 N 5 N
6 N 2 N 4 N 3 N

输出 #1

13

说明/提示

对于 20% 的数据，满足 1≤n,m≤51 1≤k≤101，所有的字符 c 都为 N。

对于 50% 的数据，满足 1≤n,m≤2001 ，1≤k≤2001 ，所有的字符 c 都为 N。

对于 100% 的数据，满足 1≤n,m≤2001 1≤k≤2001，字符 c 可能为 Y。

对于 100% 的数据，所有的 f 值满足 1≤f≤10000。

思路：

首先，在不考虑有Y类砖块时，本题就仅仅是一个背包一样的问题，但是就算有Y类砖块得加入，还是只在N处转移。面对Y类砖块，一定是能打就打的。

 

但是区别就在于，子弹本身会对后面的情况产生后效性，我们可以称之为子弹的转移，也就是打砖块的顺序发生了变化。

 

比如说，我们原本先打A，但可能此时先打B更优。这时候有一个结论：最后一个打的砖块一定为N类砖块，除非所有砖块已经打完了。 否则，你最后一个打的是Y类砖块，打完之后必定还有子弹。

 

我们在计算[1,j]列的最优解时，涉及到这些情况：

 

• 1. 第j列根本不打（直接继承[1,j−1]]的状态）
• 2. 最后一发子弹在第j列上（就是之前提过的最后一发打的子弹）
• 3. 最后一发子弹在[1,j−1]]列中
• 4. 最后一发子弹不在[1,j]]列中，此时的子弹对后面产生了后效性，但并不在此时的抉择

 

为了解决此时子弹的影响和方便计算，引入三个变量：sum1其实对应着当前列是最后一发子弹打的地方，因而以N结尾。sum2则为其余的情况：不是最后一发子弹打的地方，故而最后只能是将Y打到头。

 

而这个dp(j,k,0/1))其实表示：[1,j]列中，用k发子弹，最后一发子弹是否在[1,j]列中。（0在1不在）

转移1：dp[j][k][0]=dp[j-1][k][0],dp[j][k][1]=dp[j-1][k][1]表示这一列一个子弹都不打

转移2：dp[j][k][0]=max(dp[j][k][0],dp[j-1][k-tot[j][i]][1]+sum1[j][i]);表示最后一颗子弹打在第j列上面

转移3:dp[j][k][0]=max(dp[j][k][0],dp[j-1][k-tot[j][i]][0]+sum2[j][i]);表示最后一颗子弹打在第[1,j-1]列上面

转移4:dp[j][k][1]=max(dp[j][k][1],dp[j-1][k-tot[j][i]][0]+sum2[j][i]);表示最后一颗子弹打在第[j+1,m]列上面

 

#include<bits/stdc++.h>
using namespace std;
const int maxn=205;
const int inf=0x3f3f3f3f;
int now[maxn];
int a[maxn][maxn];
int b[maxn][maxn];
int f[maxn][maxn][2];
int sum1[maxn][maxn],sum2[maxn][maxn];
int tot[maxn][maxn];
int main()
{
    int n,m,k;
    scanf("%d %d %d",&n,&m,&k);
    for(int i=n;i>=1;i--)
    {
        for(int j=1;j<=m;j++)
        {
            char c;
            scanf("%d %c",&a[i][j],&c);
            if(c=='Y')b[j][i]=1;
        }
    }
    int ans=0;
    for(int j=1;j<=m;j++)
    {
        for(int i=1;i<=n;i++)
        {
            if(!b[j][i])
            {
                //cout<<j<<" "<<i<<endl;
                now[j]=i;
                break;//维护相连的y的最长的位置
            }
            ans+=a[i][j];
            //cout<<ans<<endl;
        }
    }
    for(int j=1;j<=m;j++)
    {
        for(int i=now[j];i<=n;i++)
        {
            sum1[j][i]=sum2[j][i]=sum1[j][i-1]+a[i][j];
            //cout<<sum1[j][i]<<" ";
        }
        //cout<<endl;
    }
    
    for(int j=1;j<=m;j++)
    {
        tot[j][now[j]]=1;
        for(int i=now[j];i<=n;i++)
        {
            int pos=i;
            while(b[j][pos+1])pos++;
            sum2[j][i]+=sum1[j][pos]-sum1[j][i];
            tot[j][pos+1]=tot[j][i]+1;
            i=pos;
        }
    }
    for(int j=0;j<=m;j++)f[j][0][0]=-inf;
    for(int j=1;j<=m;j++)
    {    
        for(int kk=1;kk<=k;kk++)
        {
            f[j][kk][0]=f[j-1][kk][0];
            f[j][kk][1]=f[j-1][kk][1];
            for(int i=now[j];i<=n;i++)
            {
                if(!b[j][i]&&tot[j][i]<=kk)
                {
                    f[j][kk][0]=max(f[j][kk][0],f[j-1][kk-tot[j][i]][1]+sum1[j][i]);
                    f[j][kk][0]=max(f[j][kk][0],f[j-1][kk-tot[j][i]][0]+sum2[j][i]);//如果不打出一枚子弹那么根本无法得分
                    f[j][kk][1]=max(f[j][kk][1],f[j-1][kk-tot[j][i]][1]+sum2[j][i]);
                }
            }
        }
    }
    printf("%d",f[m][k][0]+ans);
    return 0;
}