JSOI2019 节日庆典

题面

10pts：朴素算法：枚举每一个起点，时间复杂度\(O(n^3)\)。

40pts：玄学一点的算法：注意到当一个决策\(x\)在当前枚举到i时已经有一个决策\(y\)在\(i\)之前就小于\(x\)，那么\(x\)在后续中都不会比\(y\)优用一个栈维护最优决策点，后缀数组判定字典序大小，但是\(aaaaa\)这样的数据就能卡得体无完肤。

100pts：首先有一个结论，最优决策\(cur\)中的下标\(i-cur[j]<cur[j]-cur[j-1]\)，反证法证明：

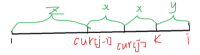
\(cur[j-1]=XXYZ\)
\(cur[j]=XYZX\)
\(cur[k]=YZXX\)

最优决策一定在\(cur[j-1]\)和\(k\)中产生，所以j不能成为最优决策。

得证。

\(cur\)中的决策在\(i\)之前都比较不出来，就循环回前缀，判断和前缀比较字典序用exkmp维护即可。