题解：洛谷 P5687 [CSP-S2019 江西] 网格图

洛谷 P5687 [CSP-S2019 江西] 网格图

题意

有一个 \(n\times m\) 的矩阵，\((i,j)\to(i,j+1)\) 花费为 \(a_i\)，\((i,j)\to (i+1,j)\) 花费为 \(b_j\)。

求出这个网格图的最小生成树。

\(3\le n,m\le3\times10^5\)，\(1\le a_i,b_j\le10^5\)。

64 解法

求最小生成树，可以直接使用 Kruskal 算法。

暴力将相邻的点连边，然后排序从前往后取。

时间复杂度

时间复杂度 \(O(nm\log(nm))\)，可以通过 \(n,m\le300\) 的数据，预期得分 \(64\)。

100 解法

先来分析题目的特殊性质。

容易发现，每一行、每一列的所有边边权都相等。

那么这个性质可以如何优化 Kruskal 算法呢？

排序

我们先考虑如何加速排序。

排序后，边权相同的边必然是连续的。这就启发我们将每一行、每一列的所有边打包成一个集合，然后放在一起排序。

但是我们最后选择的时候肯定要讨论行、列，所以需要再开一维 \(0/1\) 存储信息。

选择

然后考虑加速选择的过程。

由于排序是打包排序的，那么选择也可以试着用这种思路。

下面暂时假设处理的是行，即当前的边权是 \(a_i\)。

这行应该连多少边呢？\(m-1\) 条吗？显然不是。

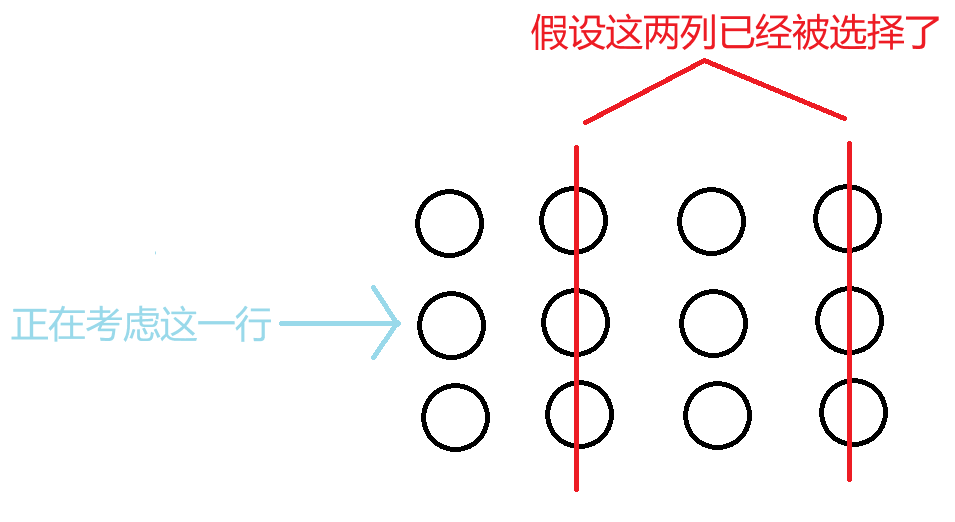
考虑上面的情况，虽然这两列已经被选择了，但是一个行都没有被选择，两列是互相独立的，所以需要连 \(m-1\) 条边才能使这一行连通。

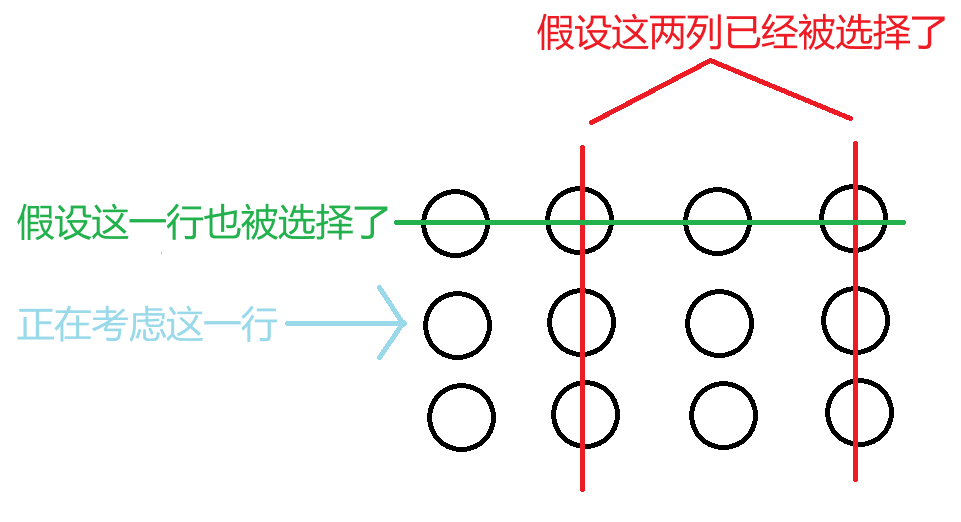
但是如果之前已经有行被选择了，那么就构成了一个连通块，两列已经连通了。那么还剩余两个点，只要将两个点挂到原来的列上就行了。

---

这就启示我们可以进行分类讨论，假设当前有 \(x\) 个行被选择，\(y\) 个列被选择。

• \(x=0\)：此时就和第一种情况一样，当前行完全没有连通，需要 \(m-1\) 条边。

• \(x\not=0\)：这个时候需要根据 \(y\) 分类讨论：

  • \(y=0\)，那么还是当前行完全没有连通，需要 \(m-1\) 条边。

  • \(y\not=0\)，那么当前行已经有 \(y\) 个点互相连通了，只需要将剩余的点连到这 \(y\) 个点即可，需要 \(m-y\) 条边。

    详细地，如果有一个点距离这 \(y\) 个点中的某一个点距离为 \(z\)，那么只需要连到距离为 \(z-1\) 的点上，然后递归下去即可。

整理一下，结论就呼之欲出了：

• \(x=0\lor y=0\)：\(m-1\) 条边。
• \(x\not=0 \land y\not=0\)：\(m-y\) 条边。

然后现在多了一个选择的行，\(x\gets x+1\)。

列同理，这里不赘述了。

结束条件

普通的 Kruskal 算法是判断剩余的点数的，但是本题中我们可以不这样做。

直接将全部的边跑完，这样子后面选不上的也不会选，正确性也是显然的。

时间复杂度

打包后边总共有 \(n+m\) 个。

• 排序，\(O((n+m)\log(n+m))\)。
• 选取，\(O(n+m)\)。

时间复杂度 \(O((n+m)\log(n+m))\)，可以通过本题，预期得分 \(100\)。

代码

/**
 * Problem: P5687 [CSP-S2019 江西] 网格图
 * Author:  OIer_wst
 * Date:    2025-07-02
 */
#include <bits/stdc++.h>
using lint = long long;
using pii = std::pair<int, int>;
const int N = 3e5 + 10;

lint ans; // ans 记录权值之和

std::vector<pii> num; // first 表示值，second=0 表示行，second=1 表示列

int n, m, row, col;

int main() {
  std::cin.tie(0)->sync_with_stdio(0);
  std::cin >> n >> m;
  for (int i = 1, x; i <= n; ++i) std::cin >> x, num.emplace_back(pii{x, 0});
  for (int j = 1, x; j <= m; ++j) std::cin >> x, num.emplace_back(pii{x, 1});
  std::sort(num.begin(), num.end());
  
  for (auto p : num) {
    if (!p.second) { // 行
      if (row && col) ans += 1ll * (m - col) * p.first;
      else ans += 1ll * (m - 1) * p.first;
      ++row;
    } else { // 列
      if (row && col) ans += 1ll * (n - row) * p.first;
      else ans += 1ll * (n - 1) * p.first;
      ++col;
    }
  }

  std::cout << ans <<std::endl;
  return 0;
}

模型归纳

打包优化的 Kruskal 算法，对于有大量权值相同时且为网格图的情况，但是可扩展性不佳。

技巧

• 将权值相同的值压缩起来一起处理。
• 动态计算贡献。