取整函数浅谈（时不时更新）

取整函数浅谈

定义

• 定义 \(\lfloor x \rfloor\) 表示 \(\le x\) 的最大整数。
• 定义 \(\lceil x \rceil\) 表示 \(\ge x\)​ 的最小整数。

函数性质

函数图像

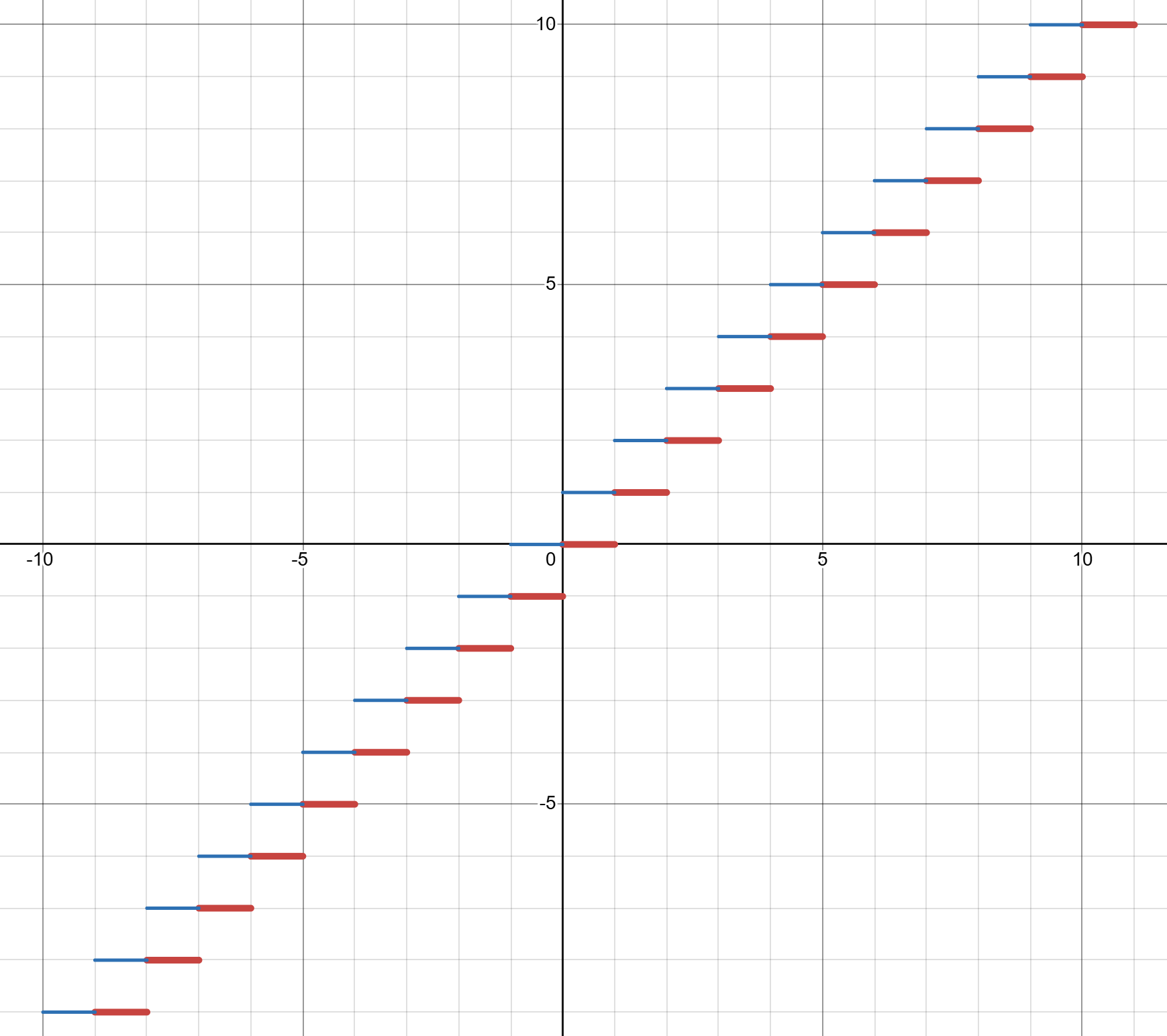
上图中红色加粗的函数为 \(\lfloor x\rfloor\)，蓝色细的函数为 \(\lceil x\rceil\)。

定义域

显然为 \(\mathbb{R}\)。

值域

显然为 \(\mathbb{Z}\)。

单调性

显然两个函数均为单调不降函数。

代数性质

• \(\lfloor x \rfloor=\lceil x \rceil=x,x\in\mathbb{Z}\)。
• \(x-\lfloor y \rfloor=\lceil x-y\rceil,x\in\mathbb{Z},y\in\mathbb{R}\)。
• \(\lceil x + y \rceil = x + \lceil y \rceil,x\in\mathbb{Z},y\in\mathbb{R}\)​。
• $ \lceil -x \rceil = - \lfloor x \rfloor,x\in\mathbb{R}$。