解不等式

高次不等式

画图，一般都问与 \(0\)（即 \(x\) 轴）的关系。

对于函数

\[y=\prod\limits_{i=1}^{n}(x-a_i)^{p_i} \]

我们可以先得到其与 \(x\) 轴的交点：\(a_1,a_2,\cdots,a_n\)。

判断穿的方向

假设当前 \(y=\left(2x-1\right)\left(x-1\right)\left(2x+1\right)\)。

则其与 \(x\) 轴交点为 \(\left(-\dfrac{1}{2},0\right),\left(\dfrac{1}{2},0\right),(1,0)\)。

但是此时我们会有两种可能的情况：

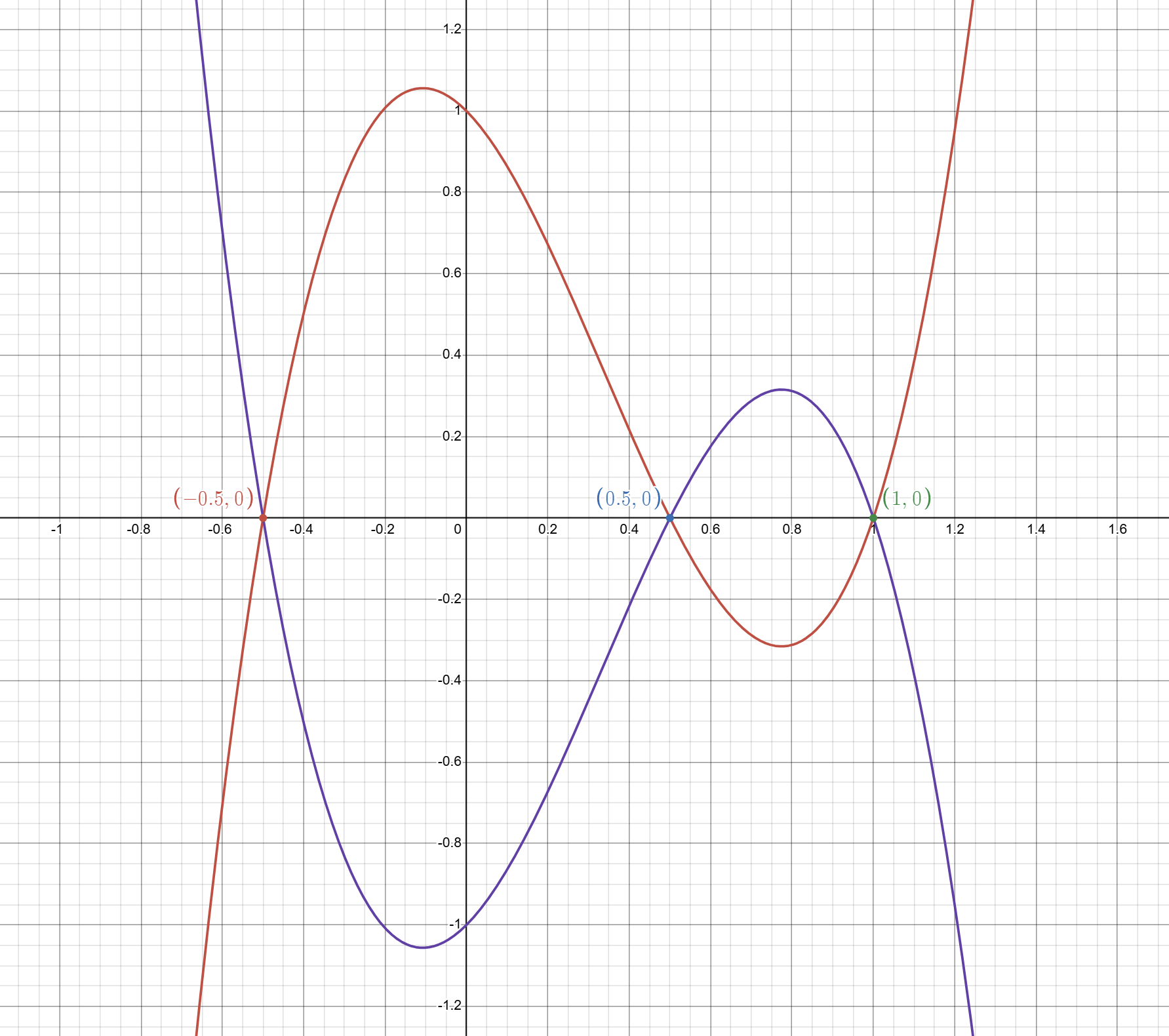
那么哪条曲线时对的呢？

可以代入值。

假设代入一个较大的值 \(x=100\)，那么显然 \(2x-1>0\)，\(x-1>0\)，\(2x+1>0\)，故函数值 \(>0\)。

图中红色曲线显然 \(x=100\) 时 \(>0\)，紫色曲线则 \(<0\)，故红色曲线正确。

最终我们也得出了 \(y=\left(2x-1\right)\left(x-1\right)\left(2x+1\right)\) 的函数图像。

当然，手绘不会那么精准，但是判断函数值与 \(0\) 的关系是无妨的。

判断是否穿过

那么给上面的函数加上一个指数，\(y=\left(2x-1\right)\left(x-1\right)^{2}\left(2x+1\right)\)，那么函数会变成什么样呢？

简单情况

令 \(y_1=x-1\)​，则图像为：

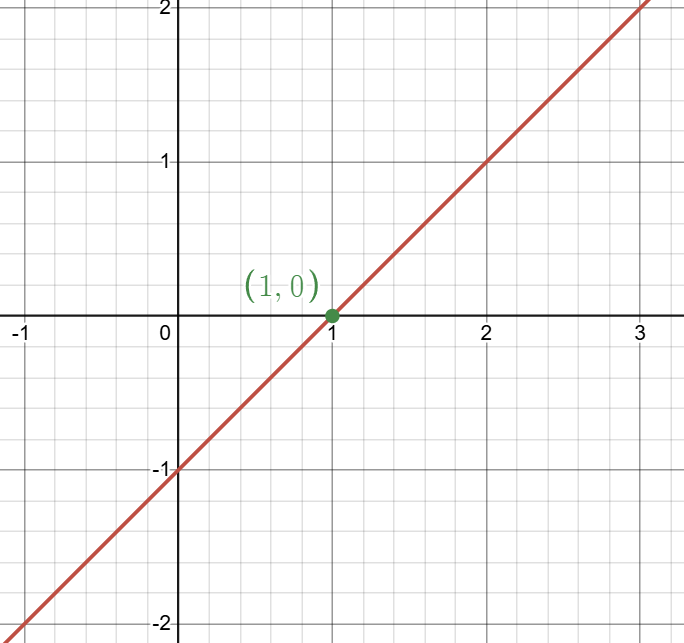
此时函数穿过了点 \((1,0)\)。

---

令 \(y_2=(x-1)^2\)，则图像为：

可以发现此时函数没有穿过点 \((1,0)\)，只是擦了一下 \((1,0)\) 就返回去了。

复杂情况

由此我们可以得出一个结论（虽然证明非常不充分，但直接用就行了）：

当 \(y\) 中一个因数为 \((x-i)^{j}\) 时，若

• \(j\) 为奇数，则函数穿过点 \((i,0)\)（如第一张图）；
• \(j\) 为偶数，则函数擦过点 \((i,0)\)（如第二张图）。

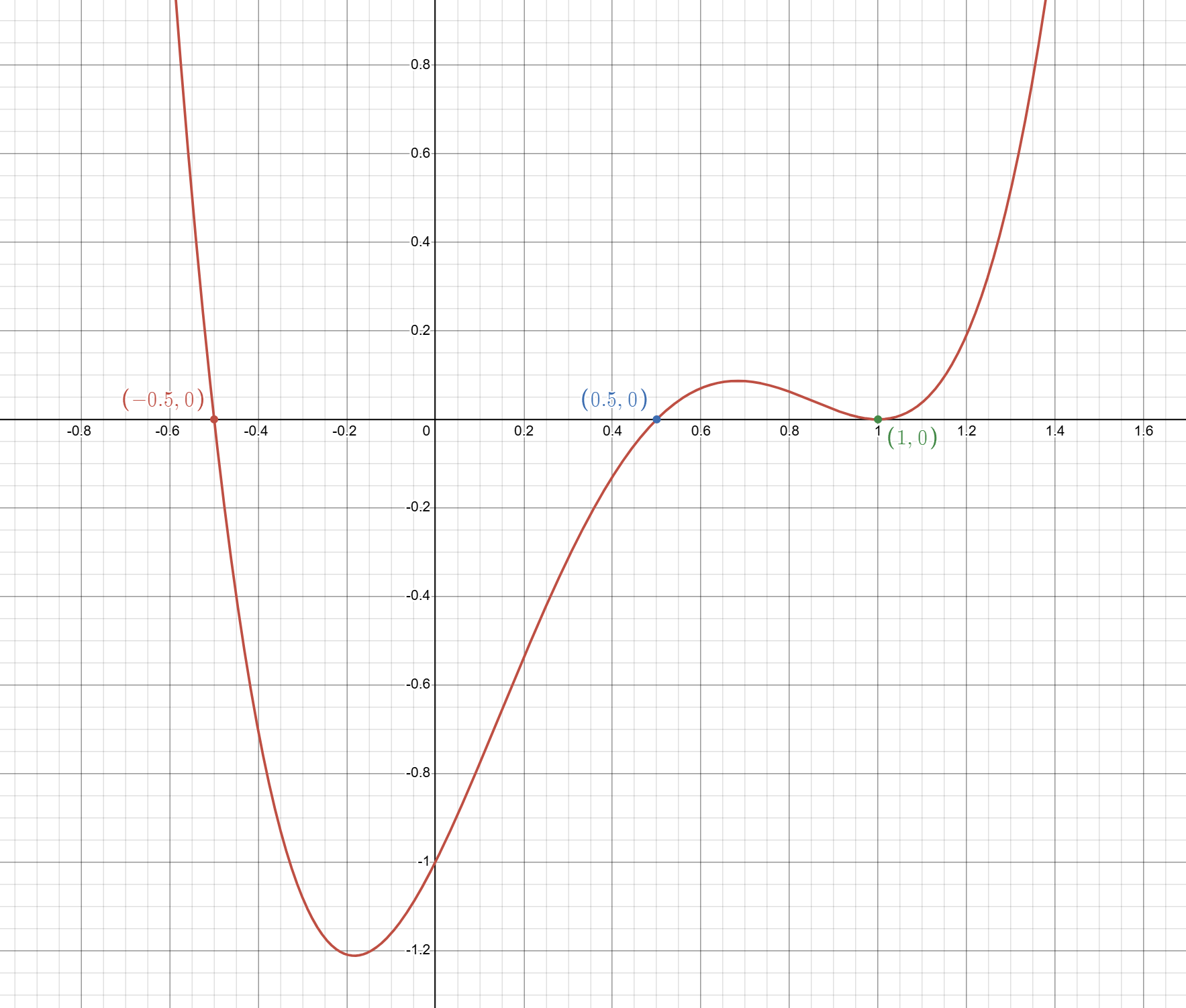
那么对于原函数 \(y=\left(2x-1\right)\left(x-1\right)^{2}\left(2x+1\right)\)，可以得到函数擦点 \((1,0)\)，穿过点 \(\left(-0.5,\ 0\right)\) 和 \(\left(0.5,\ 0\right)\)，图像如下：

总结

• 对于函数穿的方向，可以 代入具体值。
• 对于函数是否穿过，可记 奇穿偶不穿（奇数穿过，偶数擦过）。

绝对值不等式

假设当前要解的不等式为

\[|f_1(x)|<|f_2(x)| \]

则可以转化为

\[\big(f_1(x)\big)^2<\big(f_2(x)\big)^2 \]

那么移项后运用平方差公式可得：

\[\big(f_1(x)-f_2(x)\big)\big(f_1(x)+f_2(x)\big)<0 \]

分类讨论即可。